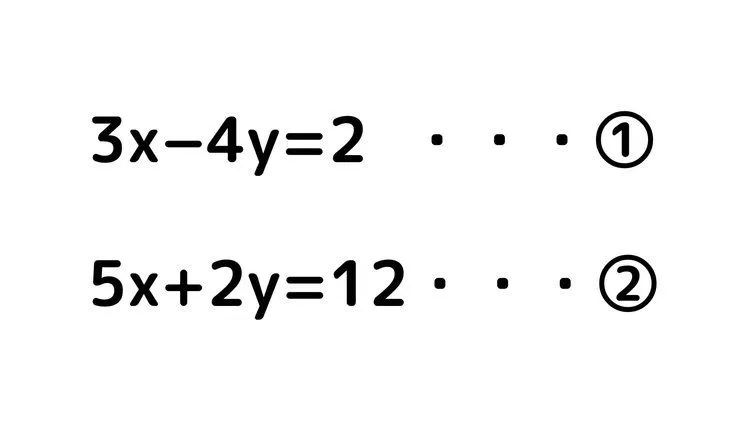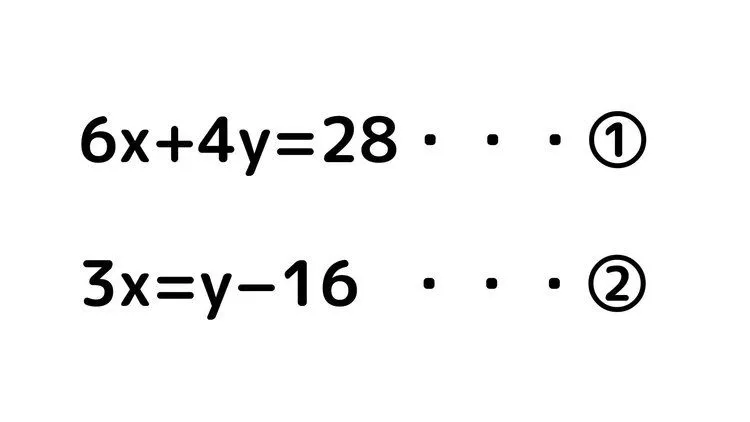明光義塾へ
学習

2025.07.01

連立方程式は簡単！基本問題の解き方から文章題の解き方まで徹底解説します

連立方程式を解く男の子

連立方程式は中学数学の重要単元で、多くの生徒がつまずいてしまうテーマです。

つまずきやすい理由は一元方程式や分数、小数など、これまでに学んだ数学の内容が一挙に出てきて総合力が問われ、また、使う文字や式が増えるため、問題が複雑になるためです。

そこで、この記事では連立方程式の解き方を練習問題を交えて、わかりやすく解説していきます。ぜひ、連立方程式を解く際の参考にしてみてください。

もくじ

連立方程式ってなに？

方程式が複数組み合わさってできているものを連立方程式といいます。

求める文字の値が1つの場合、一元方程式が1つあれば、文字の値が求まります。（文字の種類が1つの方程式を一元方程式といいます。）

一元方程式の例

一元方程式の例

求める文字の値が2つ以上になった場合、求める文字と同じ数だけ方程式を用意して、文字の値を導き出す必要があります。

(求める文字が3つの場合三元方程式と言いますが、中学数学で扱う連立方程式のほとんどが求める文字の値が2つの連立方程式です。)

連立方程式のイメージ

連立方程式を解くというのは各方程式のグラフ上の交点を求めるということです。

例えば
y=3x+5
y=-x+1
という2つの方程式が描くグラフはこちらです。

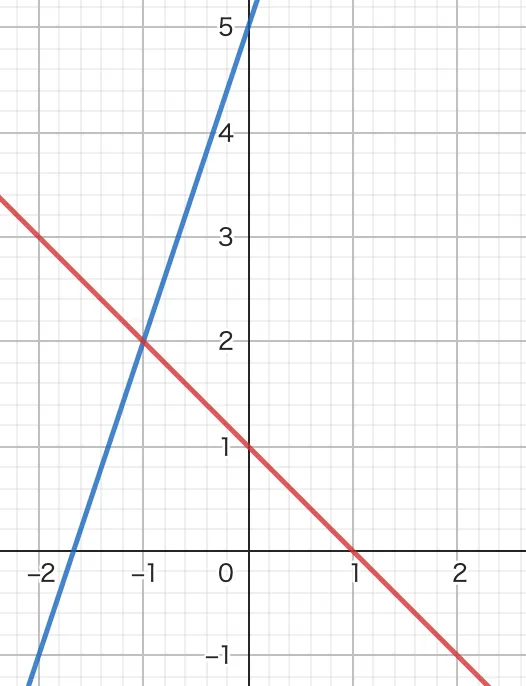
2つの直線が交わるグラフ

青い線は1つ目の方程式を満たす解の集合で、赤い線は2目の方程式を満たす解の集合です。

連立方程式を解くというのはこの2つの方程式それぞれどちらも成り立つ解x, yを求めるということです。

どちらも満たすx, yの組み合わせは交点でしかなく、直線同士の交点は1つしかできないため、1つの解が求まるということです。

実際にこの交点は(-1, 2)でそれぞれの式に代入すると、
2=-3+5
2=1+1
とそれぞれ成り立つことがわかります。

連立方程式の解き方〜その1加減法〜

加減法は与えられた方程式を足したり引いたりすることで片方の文字を消し、一元方程式に変化させる解き方です。

例題1

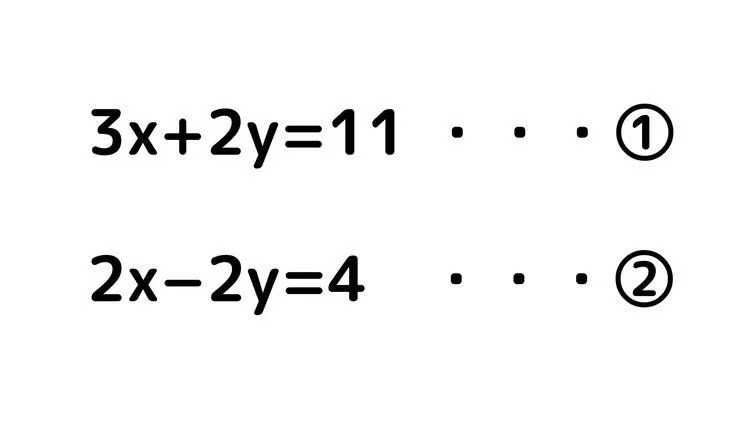
連立方程式1

文字を片方消すことが連立方程式を解くコツです。今回の問題の場合、yの係数に着目してみてください。

①の式のyの係数は2、②の式の係数は−2となっています。①の式＋②の式をすることによりyを消すことができます。

①＋②

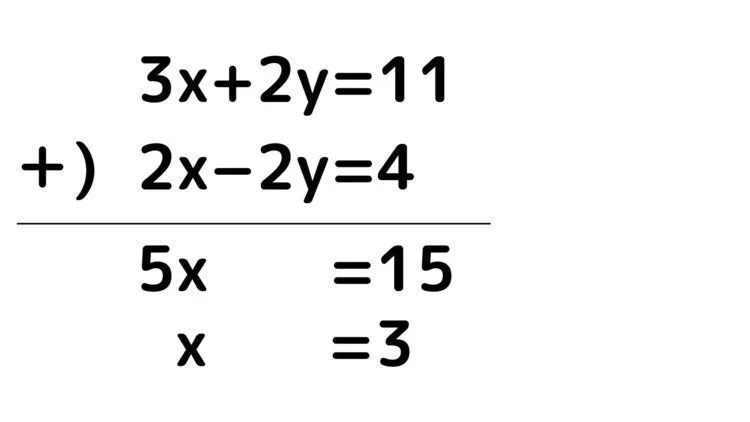
連立方程式2

yを消し、xだけの一元方程式に変化させることができ、xの値を求めることができました。

xの値を求めたら、①または②の式にx=3を代入してみましょう。今回は①の式に代入してみます。

連立方程式3

以上のようにx=3,y=1と連立方程式を解くことができました。

答えの書き方はさまざまありますが、学校で習った書き方をすれば間違いないでしょう。

例題2

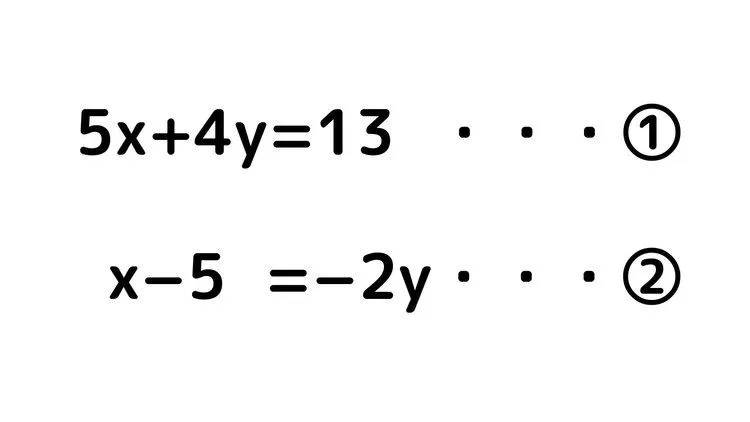
連立方程式4

今回の問題の場合はどうでしょうか。

まず、例題1と同じように式の左辺を文字の式、右辺を数字のみの式にするために移項してあげましょう。

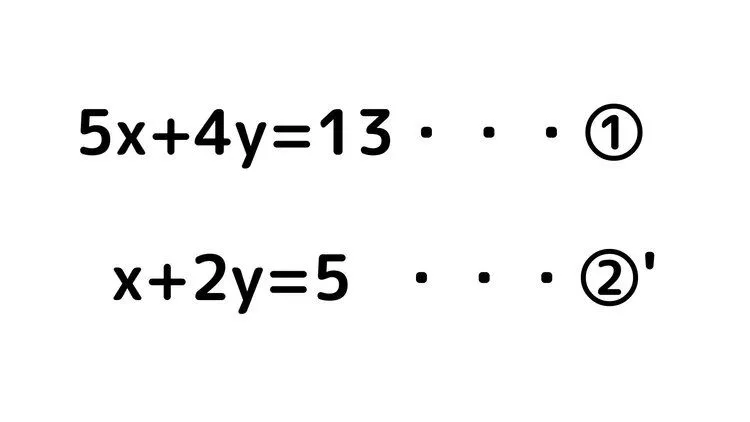
連立方程式5

例題1のように、ただこのまま足したり、引いたりするだけではどちらの文字も消すことはできません。係数が①の式と②’の式で違う場合、係数をまず揃える必要があります。

①の式のyの係数が4、②’の式のyの係数が2となっているため②’の式に2をかけることによってyの係数が揃えられます。

②’×2

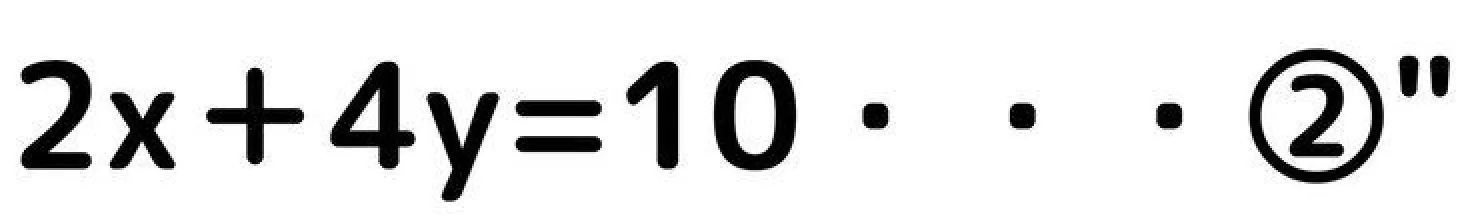
連立方程式6

yの係数を揃えることができたので計算していきましょう。

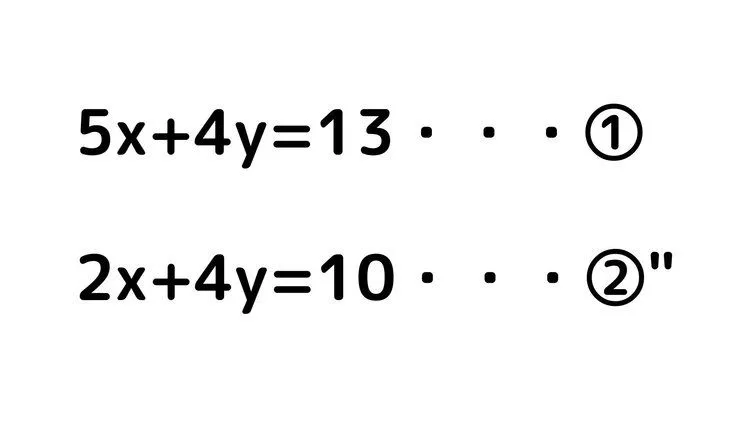
連立方程式7

yを消すためには引き算をしなければなりません。

①−②”

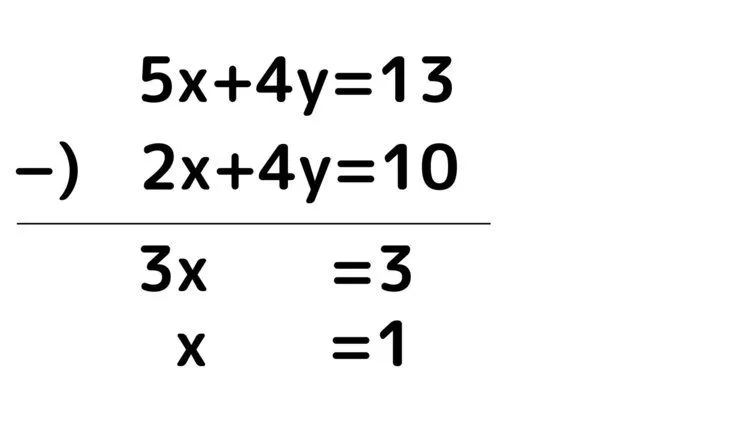
連立方程式8

xの値を求めることができました。xの値を求めたら、①または②の式にx=1を代入してみましょう。今回は①の式に代入してみます。

連立方程式9

以上のようにx=1,y=2と求めることができました。

加減法は係数を揃えて、足したり引いたりして文字を一つにすることがポイントです。係数が揃っていない場合は2つの係数の最小公倍数で揃えてあげるとよいでしょう。

加減法のおさらい

1.連立方程式の係数に注目し、どちらかの文字の係数に揃える

2.片方の文字を消すために、二つの式を足したり引いたりして一元方程式にする

3.一元方程式を解き、出てきた文字の値を使ってもう片方の文字の値を求める

連立方程式の解き方〜その2代入法〜

代入法は一つの文字で簡単な式を作って、もう一方の式に代入して片方の文字を消し、一元方程式に変化させる解き方です。

例題3

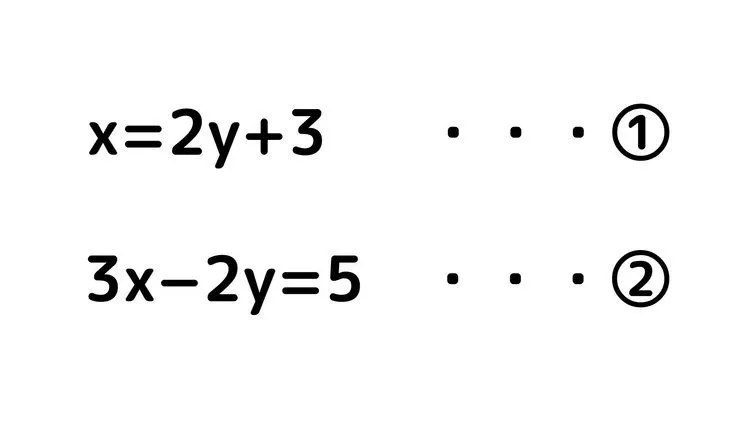
連立方程式10

この時、①の式がx=〇〇という形になっていることに注目します。代入法は片方の文字式を使って、もう一方の文字式に代入します。

この例題のようにx=〇〇やy=〇〇となっている問題では代入法を使うことで楽に解くことができます。それでは①の式を②の式に代入してみましょう。

連立方程式11

代入したことでyの値を求めることができました。それではy=-1を①の式に代入してみましょう。

連立方程式12

以上のようにx=1,y=-1と求めることができました。

例題4

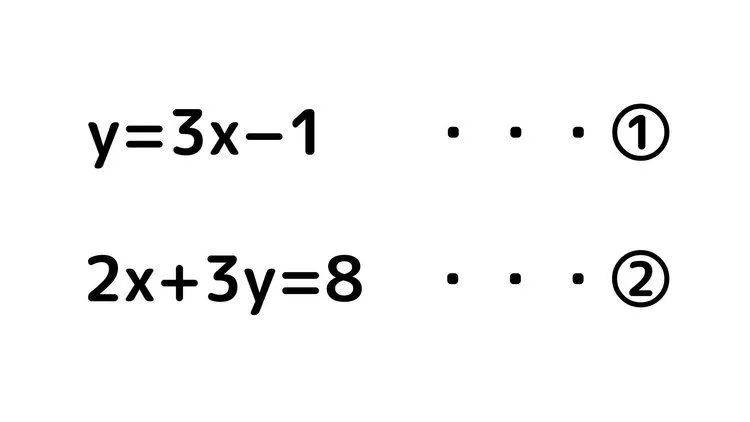
連立方程式13

①の式がy=〇〇という形になっていることに注目します。それでは①の式を②の式に代入してみましょう。

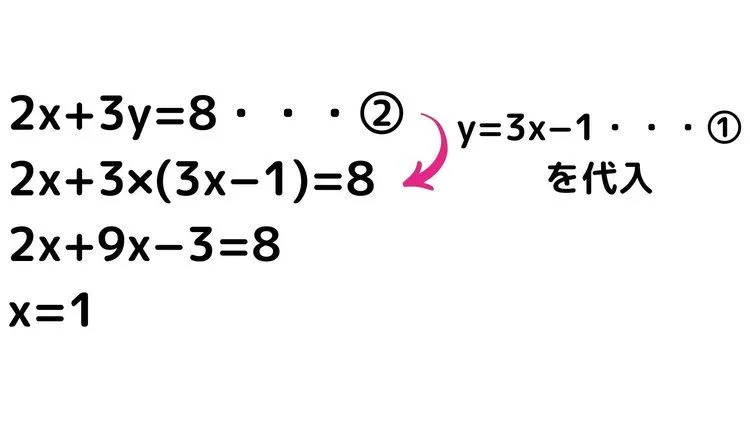
連立方程式14

代入したことでxの値を求めることができました。それではx=1を①の式に代入してみましょう。

連立方程式15

以上のようにx=1,y=2と求めることができました。

例題5

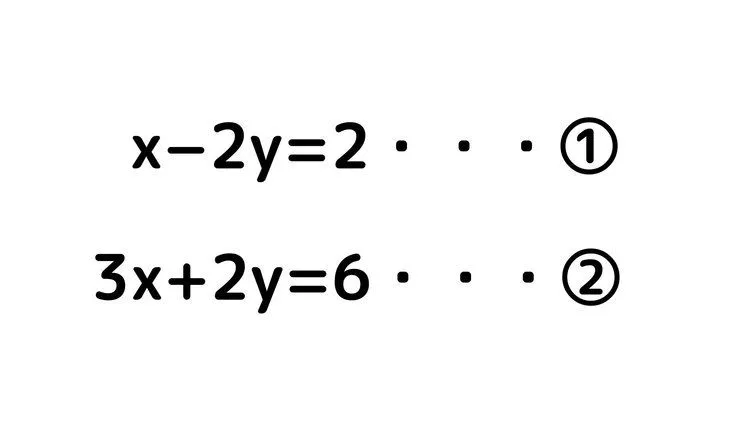
連立方程式16

今回の問題の場合はどうでしょうか。

例題3や4のようにx=〇〇、y=〇〇となっていないので、代入法を使って解く場合、x=〇〇、y=〇〇の形に移項して、直してあげましょう。

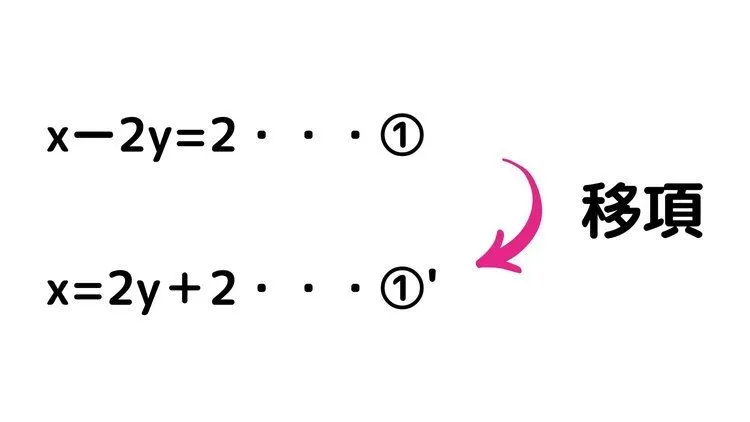
連立方程式17

x＝〇〇の形にすることができたので、後は例題3同様に②の式に代入して、文字の値を求めます。

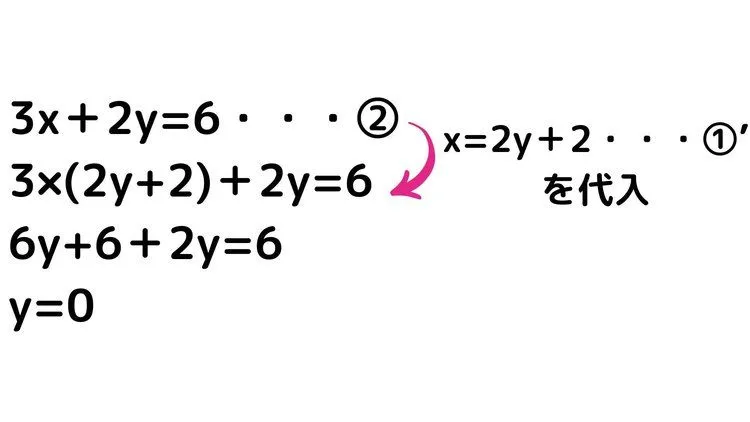
連立方程式18

代入したことでyの値を求めることができました。それではy=0を①'の式に代入してみましょう。

連立方程式19

以上のようにx=2,y=0と求めることができました。

例題6

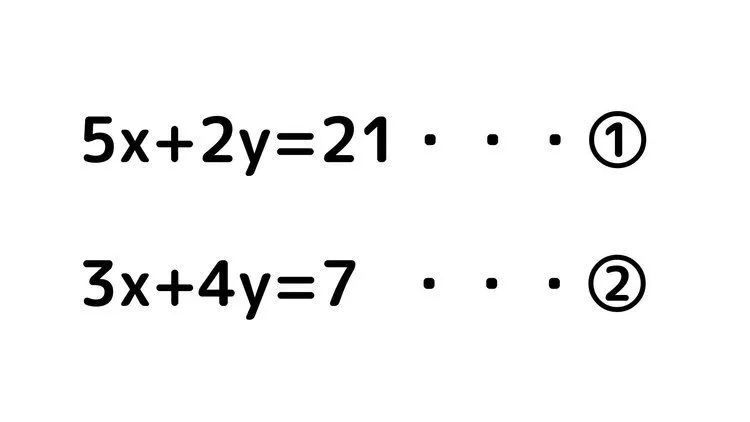
連立方程式20

今回の問題の場合はどうでしょうか。

例題3同様に①の式をy=〇〇の形にして②の式に代入しても解けますが、y=〇〇の形にすると分数が出てきて計算がめんどくさいです。計算量が増えると計算ミスも増えるので、工夫して計算してみましょう。

②の式を見てみると4yがあります。ここに注目して、まずは①の式を移項して両辺を2倍し、4y=〇〇の形にしてみましょう。

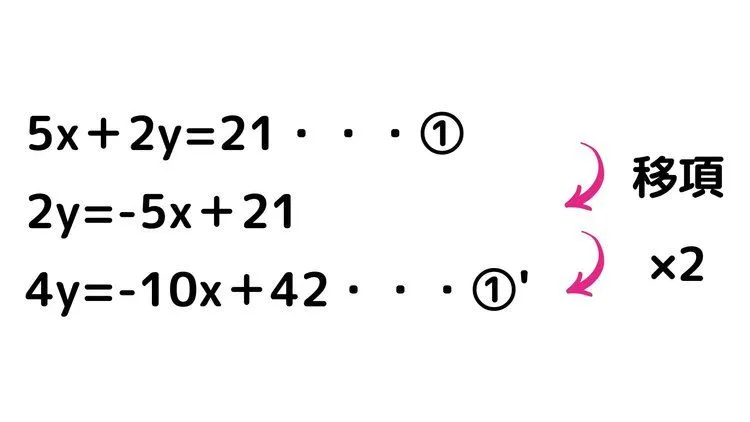
連立方程式21

では②の式に①'の式を代入してみましょう。

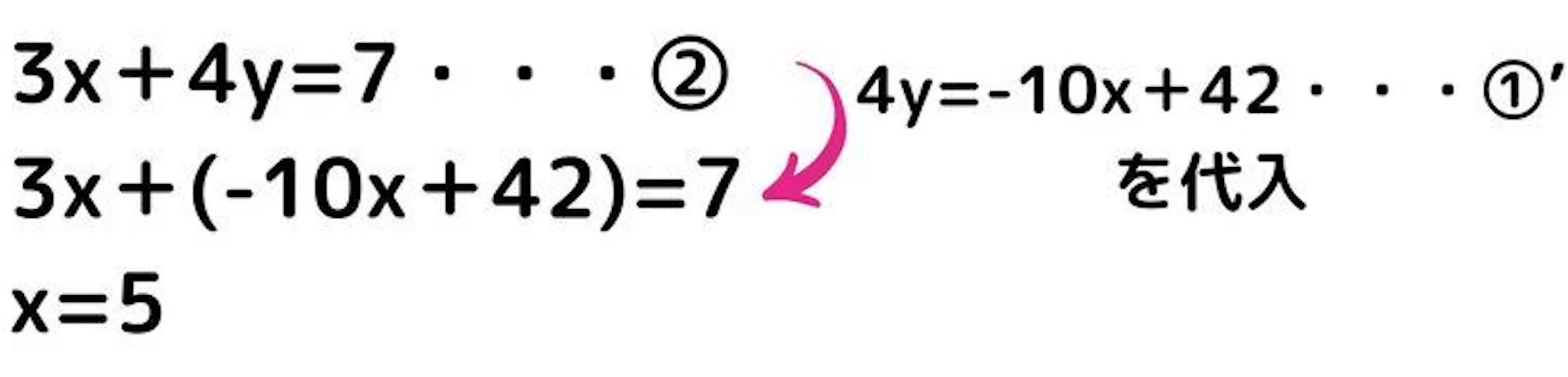
連立方程式22

代入したことでxの値を求めることができました。それではx=5を①’の式に代入してみましょう。

連立方程式23

以上のようにx=5,y=-2と求めることができました。

代入法は一つの式から、一つの文字をもう片方の文字で表す式を作り、もう片方の式に代入して、文字を一つにすることがポイントです。

代入法のおさらい

1.連立方程式を移項して、文字をもう片方の文字で表す

2.表した式をもう一方の式に代入して一元方程式にする

3.一元方程式を解き、出てきた文字の値を代入して、もう片方の文字の値を求める



連立方程式の解き方を2つ紹介しました。

代入法は計算量が多くなる傾向があるため、一般的には加減法を使って解いたほうがいいケースが多いです。ただし元の式がx=〇〇やy＝〇〇の問題の場合、代入法を使って解くほうが簡単な場合もあります。

どちらが計算量が少なくなりそうかは問題によって見極めていきましょう。

実際に解いてみよう！連立方程式の練習問題

練習問題1

連立方程式24
連立方程式_解答1

練習問題2

連立方程式25
連立方程式_解答2

連立方程式の文章題の解き方3ステップ！

連立方程式は文章題として出題されることが多いです。文章題を解くときにおさえたい3ステップを解説します。

ステップ1.「求める値」を文字で置き、単位に気をつけて連立方程式を作る

一元方程式の文章題の場合、求める値をxと置いて式を作りました。

連立方程式の場合、求める値が2つ以上になりますが基本的な式の作り方は同じです。求める値を文字で置いて式を作ってみましょう。

この時、単位に注意しましょう。方程式の両辺は同じ単位になるため、求める値の単位に注意しつつ両辺の単位が一緒になるように方程式を作りましょう。

ステップ2.片方の文字を消す

連立方程式を作ることができたら加減法か代入法を使って片方の文字を消し、一元方程式に直して文字の値を求めてみましょう。

ステップ3.最終チェックをする

答えが出たら元の式に代入して式が成り立つか確認しましょう。合っていない場合、計算ミスをしていることになるので再度連立方程式を解き直しましょう。

文章問題の解き方で確認

文章問題の例題を実際に上で説明した3ステップを使って確認していきます。

基本問題

A君がトマトを3個、キュウリを4本買うと金額は630円でした。B君がトマトを5個、キュウリを2本買うと金額は770円でした。

トマトとキュウリの値段を答えなさい。

ステップ1

文章問題ではまず求める値を文字で置きます。今回の例題の場合、求める値はトマトとキュウリの値段ですのでトマトの値段をx、キュウリの値段をyと置いてみましょう。

A君の場合、x円のトマトを3個、y円のキュウリを4本買って、金額は630円でしたので次のような式になります。


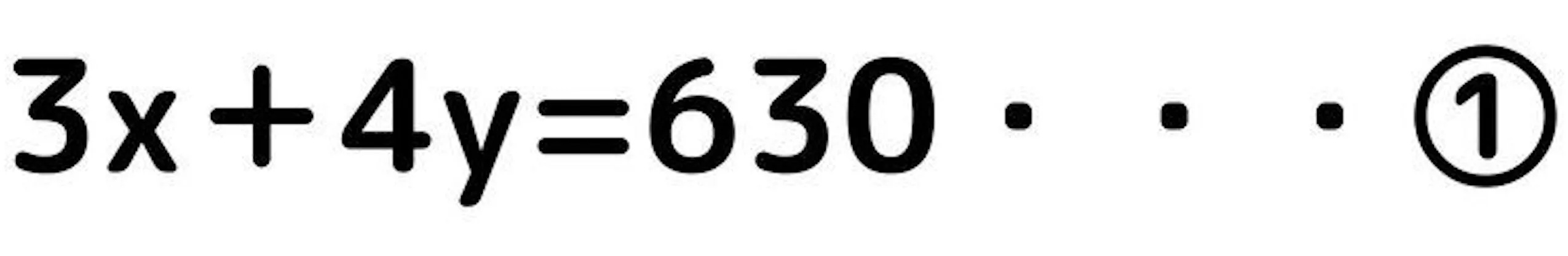
連立方程式26

B君の場合も同様に式を作ると以下の式になります。


連立方程式27

どちらの式も両辺の単位は円となり、求める文字が2つ、求める文字を含む式を2つ作れたので連立方程式の完成です。

ステップ2

実際に加減法か代入法を使って片方の文字を消し、一元方程式にして文字の値を求めてみましょう。

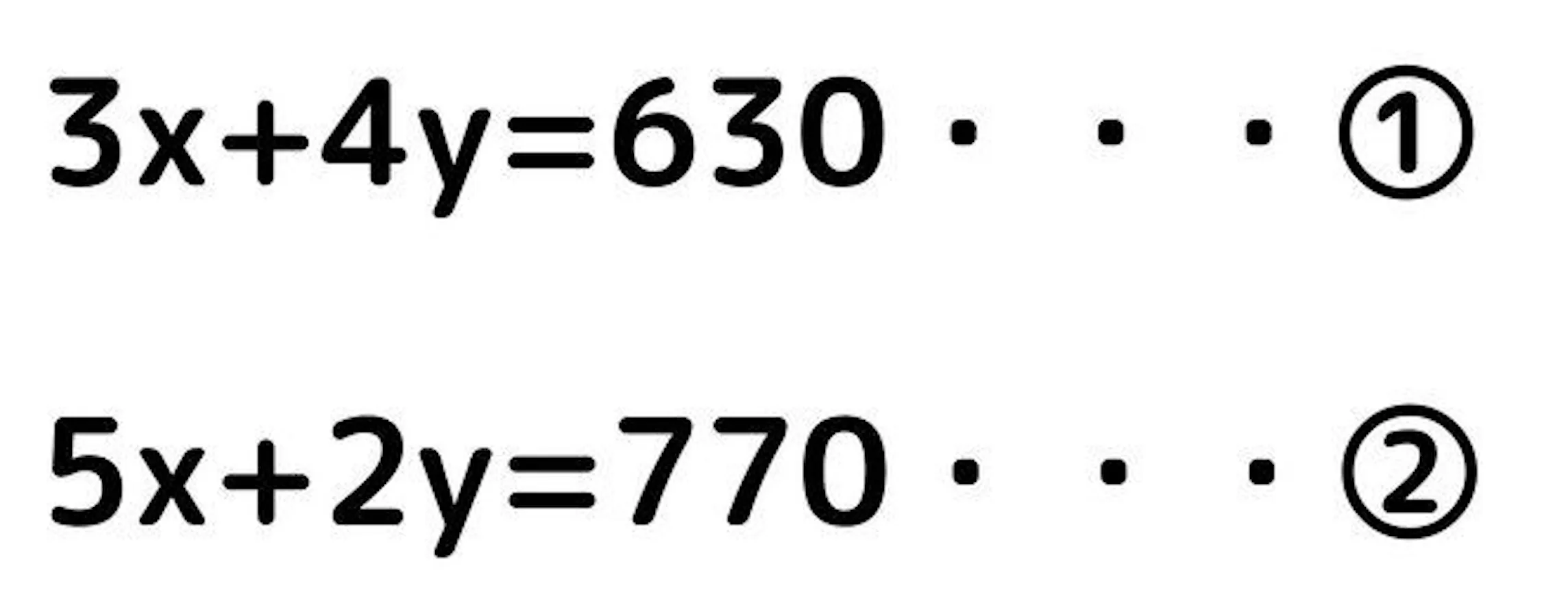
連立方程式28

加減法と代入法好きな解き方で解いてみましょう。答えはx=130,y=60となり、トマトが130円、キュウリ60円となります。

ステップ3

求める文字の値がでたら①と②の式に代入して確認してみます。①の式と②の式にx=130,y=60を代入してみて、式が成立するか試してみましょう。

連立方程式29

①と②の式両方で式が成立しましたので最終チェックもできました。

応用問題

連立方程式の文章題として頻出なのが食塩水に関する問題です。分数を使った式になり、計算が難しく感じる方も多いかと思いますが、解き方は普通の連立方程式の問題と一緒です。

では、3ステップを使って解いていきましょう。

5%の食塩水と10%の食塩水を混ぜて8%の食塩水を200g作ります。5%の食塩水と10%の食塩水をそれぞれ何g混ぜれば作れるかを求めなさい。

ステップ1

求める値を文字で置きます。今回の例題は求める値が食塩水のそれぞれの量ですので、5%の食塩水の量をxg、10%の食塩水の量をygと置きます。合わせて200gの食塩水を作るため、一つの式は

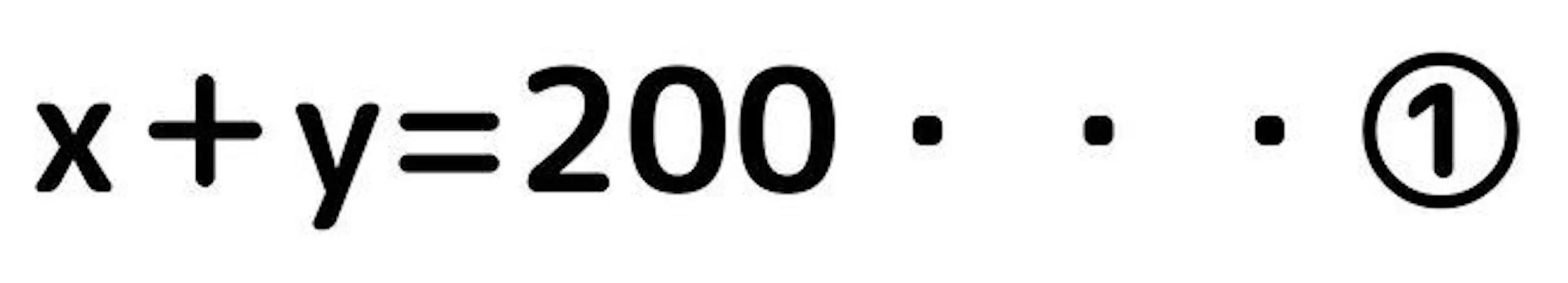
連立方程式30

となります。左辺と右辺が同じ単位(g)になることを確認しておきましょう。

次に、食塩水に含まれている食塩の量についての式を作っていきます。食塩水の濃度の%は食塩水100g中に含まれている食塩の量を表しています。よって、二つ目の式は

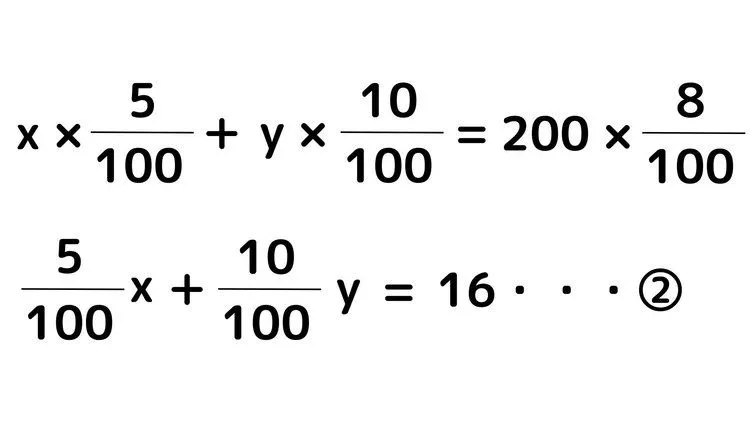
連立方程式31

となります。

求める文字が2つ、求める文字を含む式を2つ作れたので連立方程式の完成です。

ステップ2

実際に加減法か代入法を使って片方の文字を消し、一元方程式にして文字の値を求めてみましょう。

まず、②の式が分数になっていてそのまま計算すると大変なので、両辺に分母の100をかけて分母を消します。

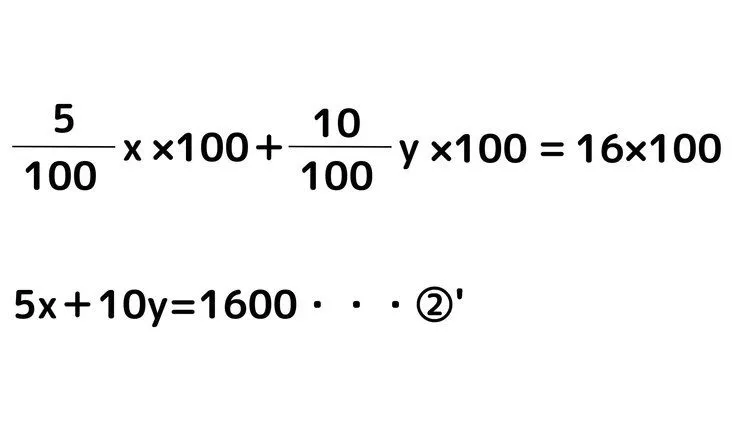
連立方程式32

加減法と代入法、好きな解き方で解いてみましょう。答えはx=80,y=120となり、5%の食塩水を80g、10%の食塩水を120g混ぜると8%の食塩水を200g作れるということになります。

ステップ3

求める文字の値がでたら元の式に代入して確認してみます。①の式と②’の式にx=80,y=120を代入してみて式が成立するか試してみましょう。

連立方程式33

①と②'の式両方で式が成立しましたので最終チェックもできました。

文章から連立方程式を作るのには慣れが必要です。たくさんの問題を解くことで連立方程式の文章問題に慣れていきましょう。

練習問題

次の2つが描くグラフの交点を求めよ
y=2x+1
y=-4x+2
連立方程式_解答3
次の連立方程式を解きなさい
3x+2y=1
x-2y=3
連立方程式_解答4
次の連立方程式を解きなさい
7x+y=1
x=-y+1
連立方程式_解答5
ある中学校で、生徒Aと生徒Bがそれぞれ募金活動を行った。生徒Aは1人あたり100円ずつ、Bは1人あたり150円ずつ集めることにした。AとBを合わせると20人が募金に協力し、合計で2,500円集まった。このとき、Aの協力者は何人で、Bの協力者は何人だったか？
連立方程式_解答6
8%の食塩水と12%の食塩水を混ぜて、10%の食塩水を300g作りたい。このとき、それぞれの濃度の食塩水を何gずつ混ぜればよいか、求めなさい。
連立方程式_解答7

まとめ

連立方程式は加減法と代入法の2つの解き方と、文章題を解く上での3ステップを理解していれば決して難しい問題ではありません。

連立方程式の問題を解くことで整理して考える力が身につくようになります。

この記事の内容を参考にしてたくさん連立方程式の問題にチャレンジしてください。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

この記事を家族や友人に教える

明光プラスで読みたい記事のテーマを募集

明光プラスでは読者の方のご期待に沿えるように読みたい記事のテーマを募集しています。ぜひ下のリンクからアンケートにお答えください。

読みたい記事のテーマをリクエストする

関連タグ

#中学生 #数学

あわせて読みたい記事

タグ一覧

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

Home > 明光プラス > 学習 > 連立方程式は簡単！基本問題の解き方から文章題の解き方まで徹底解説します