高校生

2023.11.21 2023.11.28

微分とは一体何なのか？微分はただの○○です！

高校数学の教育課程で避けては通れない微分。苦手に感じていたり、つまずいたりしてしまう方も多いのではないでしょうか。

そこで本記事では、微分とは一体何なのかをわかりやすくかみ砕いて紹介し、微分の基礎的な公式も一覧にして紹介しています。

この記事を読んだ方が微分の内容を理解することによって、微分に対する苦手意識がなくなり、応用問題に取り組める力がつくようになると幸いです。

微分とは？

教科書でよくこのような式を見かけませんでしょうか。

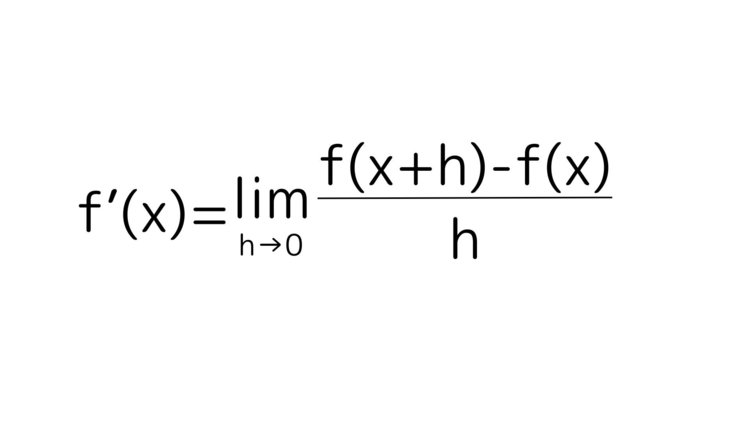
この式だけを見ても意味が全くわからない人もいらっしゃるのではないでしょうか。このように微分を教科書に載っている定義だけで理解しようとするととても大変です。後々この式の意味がわかりますので、「こんな式があるんだな」くらいに思っておいてください。

微分とは結論から先に言うとただの「傾き」です。

傾きとは、中学生の時に習った一次方程式y=ax＋bにおけるaの部分を表しています。xの値が1増えたらyの値がどのくらい増えるのか、というのが傾きです。

しかし、世の中にあるグラフは、このような中学生の頃に習った一次方程式のように簡単になっていることは非常に少なく、傾きを簡単に求めることができません。

例えば、車で40kmの距離を移動して、1時間で目的地につきました。車は時速何kmで走行していましたか？という問題があったとします。1時間で40km走ったのであるならば、答えは時速40kmでしょ？と言いたくなりますが、実際、車は一定の速度で走行しているわけではありません。y軸を距離、x軸を時間とした時、車の走行した距離のグラフは例えばこのようになります。

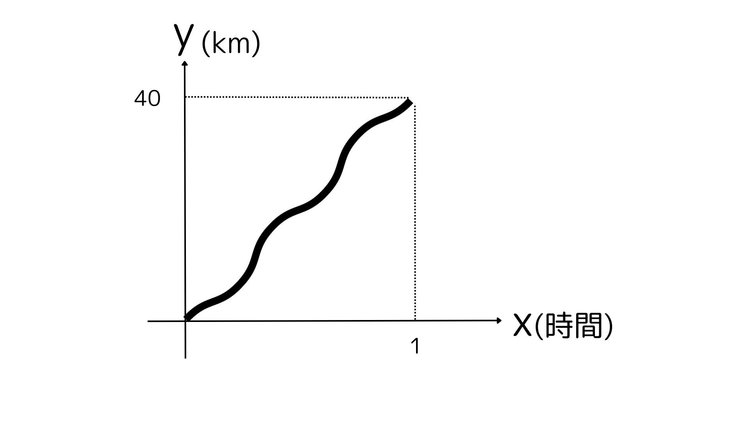
1時間の間、同じ時速40kmで車が走行していた場合は、以下のグラフの赤い線で表せます。赤い線を式で表すと、xが1(時間)進むとyが40(km)増えることになるのでy=40xとなります。

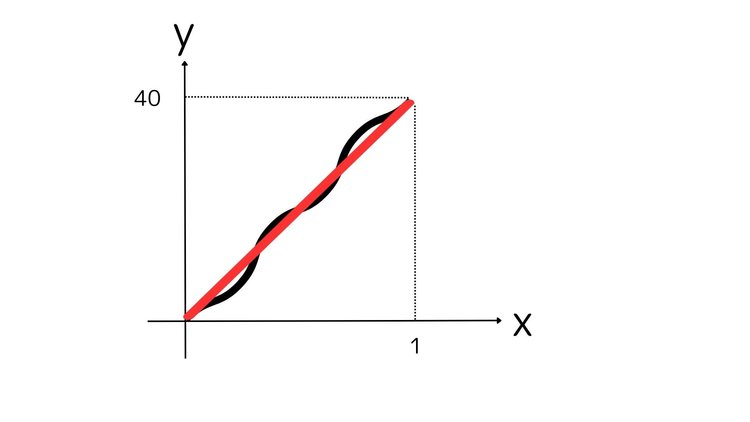
1時間ずっと同じ時速で車が走っていたらこの考えになります。これを平均時速といい、数学では平均変化率といいます。でも、実際には、高速に乗っていたり、赤信号で止まっていたりするので、その時々によって車のスピードメーターが示す速度は違うはずです。

その時々のスピードメーターの値、つまりグラフの傾きを求めることができるのが微分なのです。例えば、この時の車の速度を求めるとしましょう。

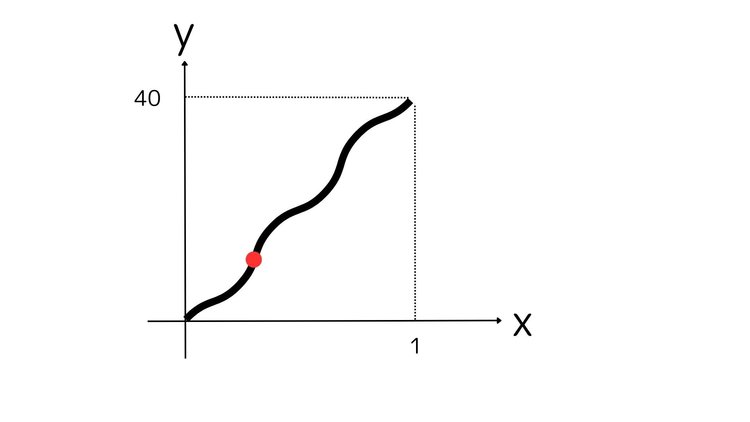
傾きを求めるときはa= yの増加量 xの増加量で求めることができました。y=f(x),xの増加量をhとすると(高校数学では増加量をよくhやΔxで表します)

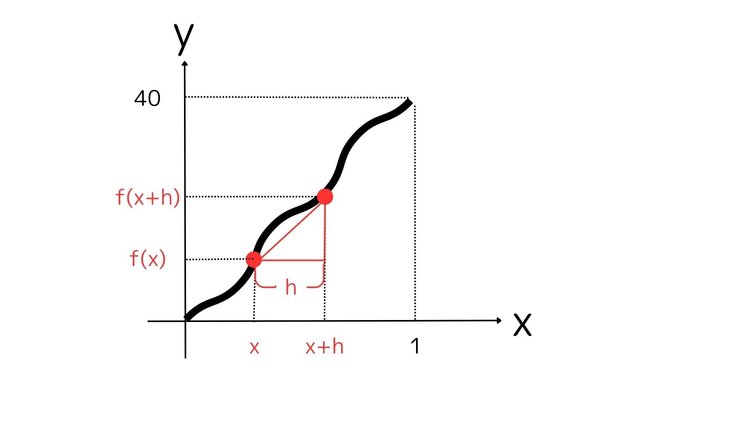
となります。

ただ、上のグラフをよく見ると求めた傾きよりもxの時点での傾きの方が急に見えませんか？hの値が大きめにとられているため、xの時点での傾きではなく、平均の時速になっているからです。

ではhをもう少し小さい値にしてみましょう。

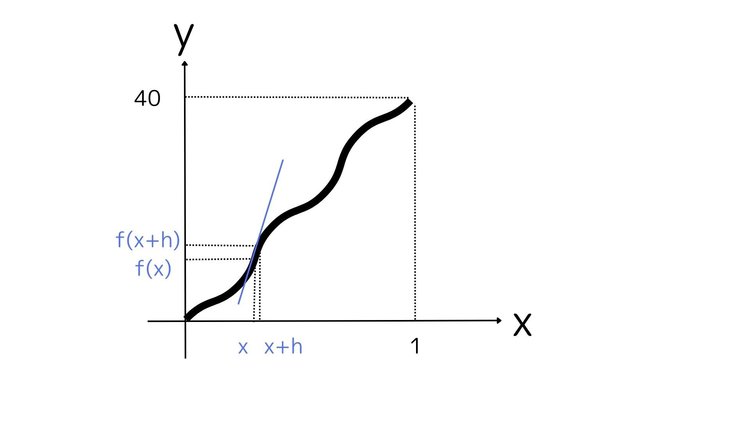
xの時点でのグラフの傾きと直線の傾きが近くなってきました。その瞬間の速度を出すために、上のグラフのようにhの値を極限に小さくすることで、その瞬間の傾きを求めよう、つまり関数の変化の割合を求めるというのが微分の考え方なのです。

微分では、ある一点における傾きを求めるために、まず2点の間の傾きを求めるという考えのもと、先ほどのようにhというxの変化量を置きます。その後、点における傾きを表すためにhの値を極限に0に近づける作業をしていきます。

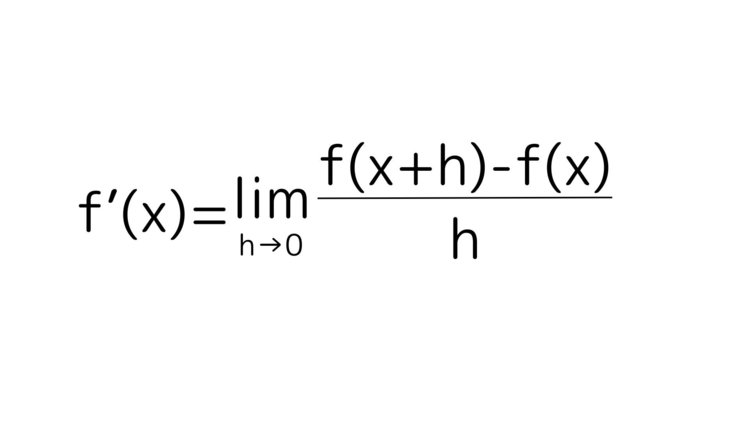
ここで先ほどの微分の定義の式をもう一度見てみましょう。

f’(x)はf(x)を微分したもの、limは極限を表し、下にあるh→0と合わせて、hを限りなく0に近づけるという意味です。そうするとこの式が表していることはxの時点での傾きを求めているということになります。

基本的な関数の微分(導関数)

では、f(x)が具体的な関数として表される時に、どのように計算すればよいのかを実際に確認していきましょう。

f(x)を微分して得られる関数をf’(x)とよく表し、導関数と呼びます。f(x)=x²のときの導関数を求めてみましょう。

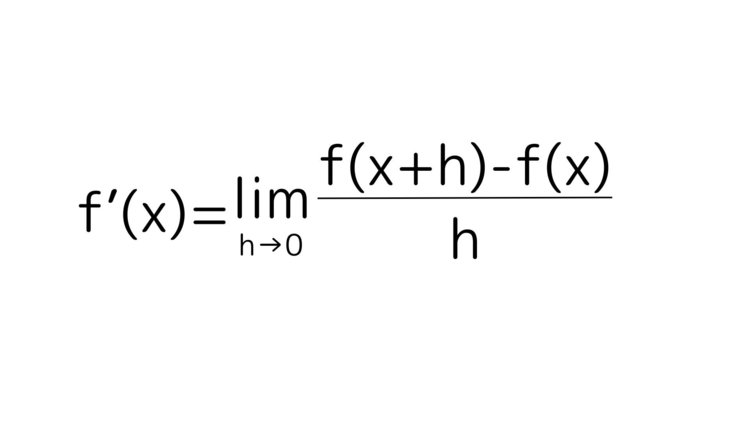
導関数の定義はこの式でしたのでf(x)=x²のとき、xにそれぞれx+h,xを代入すると、f’(x)はこのようになります。

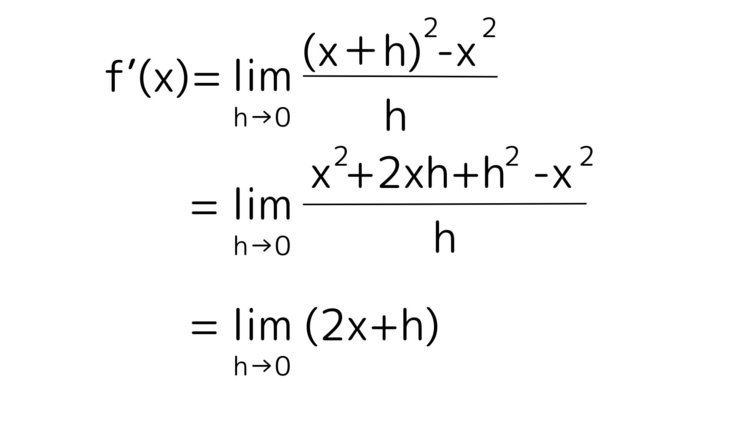
ここで、h=0に限りなく近づけると(h=0を代入すると)f’(x)=2xと求まりました。

※なぜhを限りなく0に近づける、という言い方をするのかと言うと、数学では0で割ることはご法度だからです。もともとの式ではhが分母にあるため、h=0とすると0で割ってしまうことになります。計算上はhで約分をした後に、h=0を代入すると考えても問題ありません。

以上のように、高校生の数学では、導関数をすべて同じように計算すれば求めることができますが、実際のテストではよく出てくる導関数の公式は暗記しておいたほうがよいです。

それでは、基本的な導関数の公式を一気に紹介していきます。導関数はf’(x)だけでなく、 df(x) dx や(f(x))’のように表されることもあるので覚えておきましょう。

数学IIの範囲の微分公式

(x^α)’=αx^{^α-1}

αがマイナス(分数)のときでも成り立ちます。αが正のときは、二項定理から導出することができます。

数学IIIの範囲の微分公式

三角関数の導関数(微分)

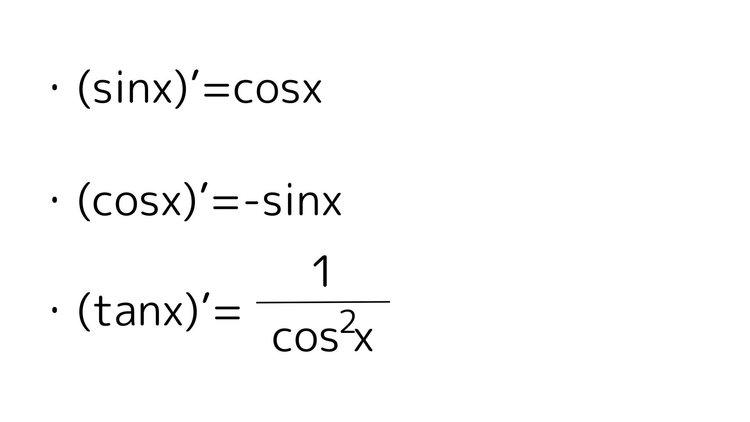
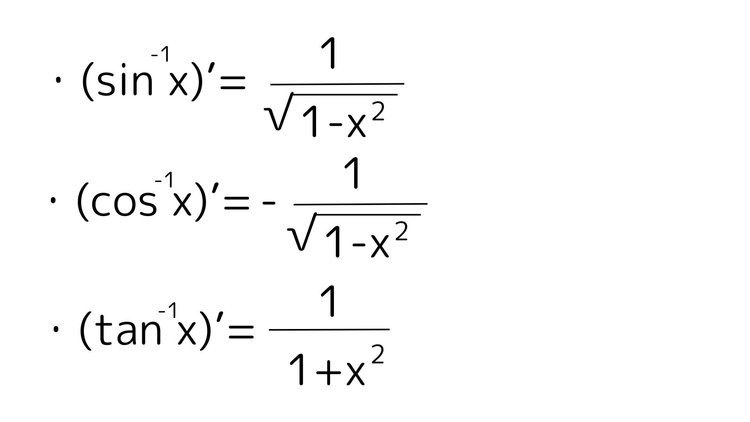
指数・対数の導関数(微分)

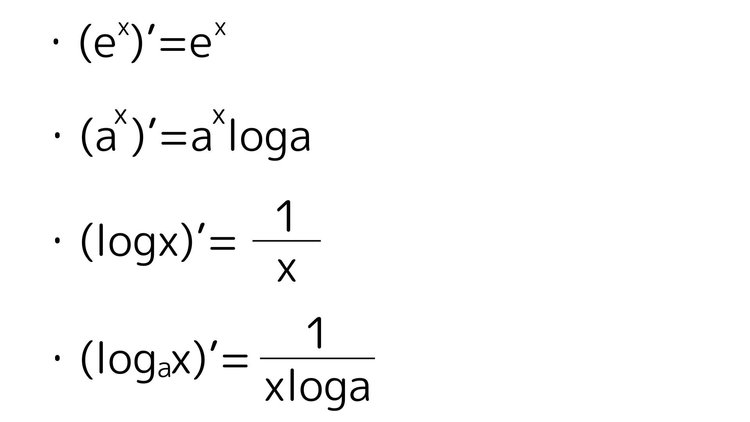
基本的な演算

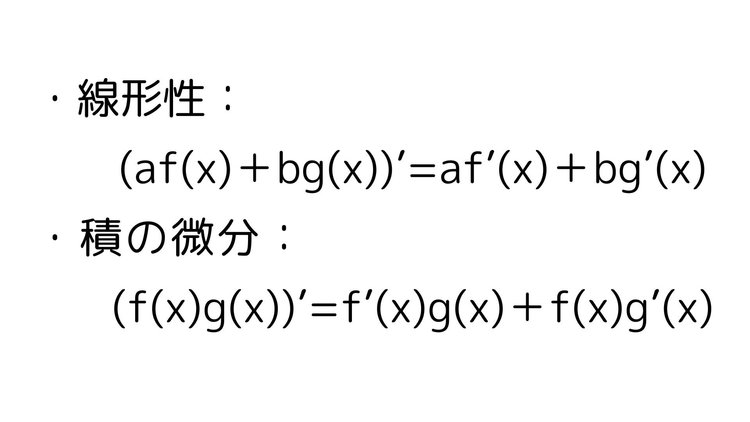
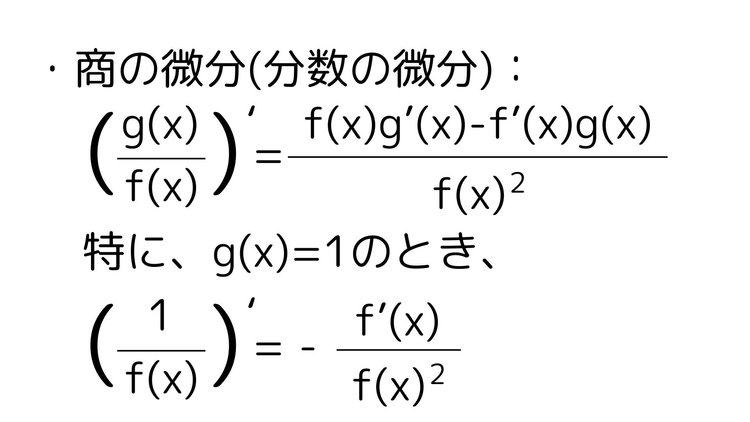
微分の使用例

ここまで微分の基礎を紹介しました。ここからは微分をすることで一体何ができるのか、その一部を紹介します。

関数の中の最大、最小がわかる

微分をすると傾きを求めることができます。傾きの正負や、0になるところがわかると、関数がどのような形のグラフになるのかを想像することができます。

よく使われるのが増減表と呼ばれる以下のような表です。

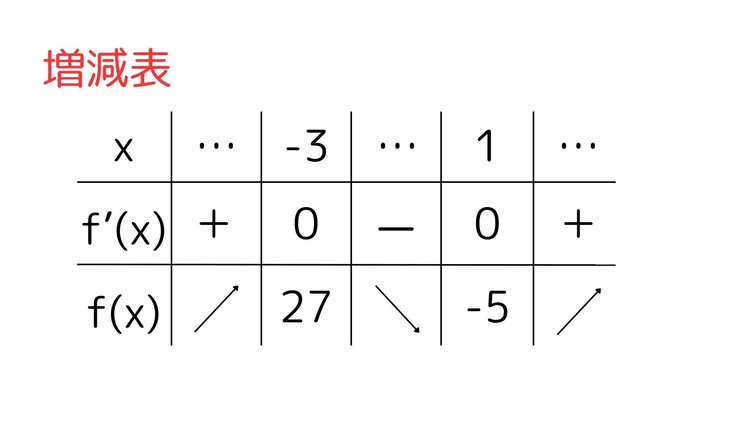
導関数が0になるxの値を求めて、そこからxの値が増えた部分、減った部分の傾きがどうなっているのを示している表です。この表からf(x)の値は、x=-3までは増え続け、そこから1になるまで減り、それ以降は増え続けるというグラフだということがわかります。おおよそですが、下記のようなグラフになると想像することができます。

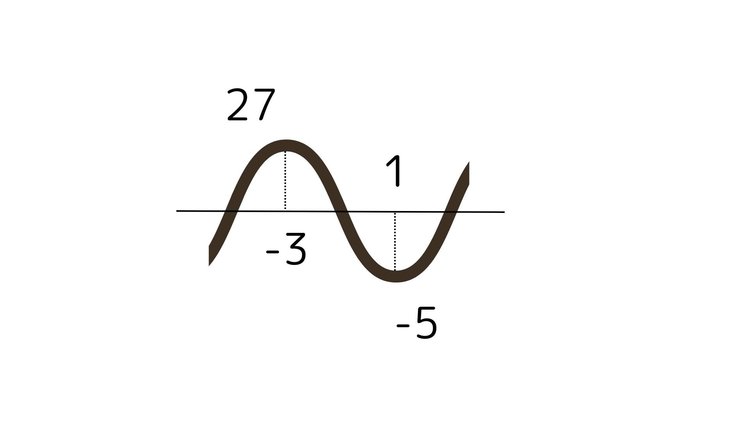
このときのグラフの凸の部分を極大といい、凹の部分を極小と言います。

基本的に関数の最大値はこの極大部分か、xの範囲の最小値・最大値のどちらかになります。(今回のグラフの場合は極大より左側は極大値より小さくしかならないので、xが最大のところか、極大部分のどちらかが最大値になります。)

同様に、関数の最小値は極小部分か、xの範囲の最小値・最大値のどちらかになります。(同様に、極小より右側は極小値より大きくしかならないので、xが最小のところか、極小部分のどちらかが最小値となります。)

まとめるとこのようになります。

1.導関数を求める
2.f’(x)=0になるxとf(x)の値(極大・極小)を計算する
3.極大・極小の左右でf’(x)の値が＋なのか−なのかを求める
4.グラフの傾きを矢印で表現する
5.範囲の中で最大・最小を求める(極大・極小とxの最小値・最大値によるf(x)の値のいずれか)

解答はこちら

曲線の接線と接点が求められる

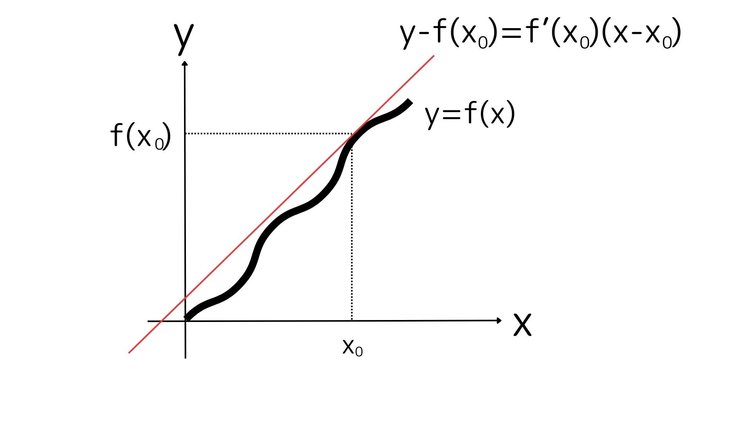
接線とは曲線のその点での傾きをもつ直線です。一次方程式で習いますが、(x₀,y₀)を通る傾きaの直線の式は以下のように表されます。

y−y₀=a(x−x₀)

このaは傾きであったため、微分を使うことでaはf’(x)と表すことができます。また、y₀=f(x₀)であることから微分の分野でのx₀での接線の方程式は以下のようになります。

y-f(x₀)=f’(x)(x-x₀)

また、この考えを応用して、ある関数がもつ実数解の個数を導く問題があります。

例えば、方程式x²-2ax+4a-3=0において、aが変化する場合、実数解の個数をaの範囲を用いて示せ、という問題があるとします。このような場合は、方程式を直線の方程式(xの一次式と)とそれ以外に分けてあげます。

f(x)=x²
g(x)=2ax-4a+3

x²-2ax+4a-3=0の式はf(x)-g(x)=0と表され、移項したf(x)=g(x)を求めることと同じことを意味しています。このとき、f(x)とg(x)の交点の数が実数解の個数を表すことになるため、その考え方を使って、f(x)=g(x)が実数解をもつパターンについて考えます。

g(x)=2a(x-2)+3と変形でき、(2,3)を通る傾き2aの直線だとわかります。

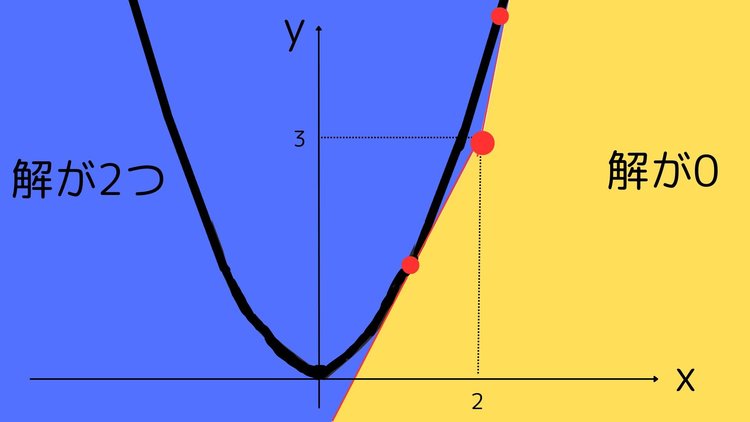
グラフを見ればわかるように、f(x)と接する場合に解(交点)が1つ、f(x)とg(x)が交わる場合に解(交点)が2つとなり、f(x)とg(x)が交わらない場合には解(交点)を持ちません。では、それぞれの場合におけるaを求めるために、まずはf(x)とg(x)が接するaの値を求めていきます。接するということは

f(t)=g(t)・・・①
f’(t)=g’(t)・・・②

となる実数tが存在するので②より

2t=2a
t=a

これを①に代入して

a²=2a²-4a+3
a²-4a+3=0
(a-1)(1-3)=0
a=1,3となりました。

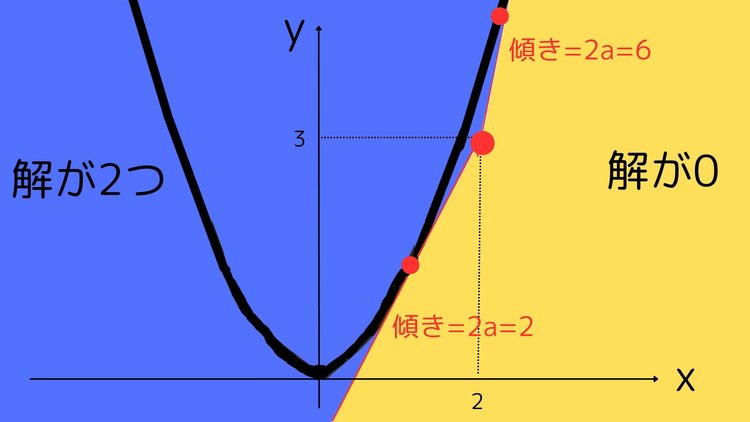
上の式より、
a=1,3のとき実数解1個

また、上のグラフからわかるように、1＜a＜3の範囲にaがあるとき、直線がf(x)に接さないことがわかります。
よって、1＜a＜3のとき実数解0個

逆にこれ以外の範囲にaがある場合、f(x)と直線が交わることがわかります。
よって、a＜1,3＜aのとき実数解2個

以上のことから
1＜a＜3のとき実数解0個
a=1,3のとき実数解1個
a＜1,3＜aのとき実数解2個
となることがわかります。

まとめ

いかがでしたでしょうか。微分の定義から簡単な公式、使い方まで紹介しました。

微分を苦手な方も多いと思いますが、微分は高校数学で避けては通れない重要な単元の一つです。微分は瞬間の傾きや速度、関数の最大値・最小値、接戦や接点を求めることができます。

この記事を読んだ方が微分の本質を理解し、微分の解き方をマスターできるようになる手助けとなれば幸いです。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

あわせて読みたい記事

総合型選抜とは？AO入試との違いや受かる人の特徴をわかりやすく解説！

高校生

2024.04.26

総合型選抜は2021年から名称が変更され、前身のAO入試と比べ内容も変わってきました。国公立・私立共に導入する大学・学部が年々増えてきており、文部科学省「令和5年度国公私立大学・短期大学入学者選抜...
【簡単】二次方程式の解の公式と、判別式についてやさしく解説します！

中学生

高校生

2024.04.19

中学3年生で習う公式の1つに二次方程式の解の公式があります。解の公式を自由自在に操れると、二次方程式の解をすぐに出せるようになります。しかし、解の公式には平方根や分数が出てきます。単純に計算として...
因数分解はなぜ必要？因数分解の意味とやり方、公式を1から解説！

中学生

高校生

2024.03.12

中学3年生や高校の数学で習う文字と式の単元で出てくるのが因数分解です。共通因数や定数項など聞き慣れない言葉が説明で多く出てくるのに加え、覚えておかなければいけないテクニックが複数あります。意味や公...