2024.04.14

素数とは○○です！覚えておくべき素数一覧や素数の判定法を紹介！

素数は中学1年生で初めて習いますが、大学入試でも素数に関する問題はよく出てきますし、歴史的に多くの数学者によって研究されてきましたが、いまだに解明されていないことがたくさんあります。

単純なようで奥深い素数とは一体なんなのでしょうか。
この記事では素数について何も知らない人でも理解できるように簡単に解説します。

素数とはあるルールを満たす数のこと

偶数が2で割り切れるものというように、素数もあるルールを満たす数のことを言います。
素数の定義は「自然数の中で1とその数自身以外に約数が無いもの」で、簡単に言うと「割り切れる数が無いもの」が素数です。
割り切れるという概念は自然数(整数)特有のものですし、1とその数自身ではすべての整数が割りきれるため、「自然数の中で」や「1とその数自身以外に」という細かい説明が入っているだけのことです。
少し回りくどいために、すんなりと理解するのが難しいかもしれませんが、例を用いて理解すると拍子抜けするほど簡単です。

ここで正の整数である10が素数かどうかを判定します。

10の約数は10を割り切ることができる正の整数なので、1, 2, 5, 10です。
ここで素数の定義と照らし合わせてみると
1とその数(10)以外の約数があるため10は素数ではありません。

次に7について素数かどうか判定します。

7の約数は1, 7のみです。
１とその数以外に約数がありませんね。
なので7は素数です。

100までの素数一覧

素数は無限にあることがわかっていて、すべての素数を紹介することは不可能なので100までの素数を一覧にして紹介します。
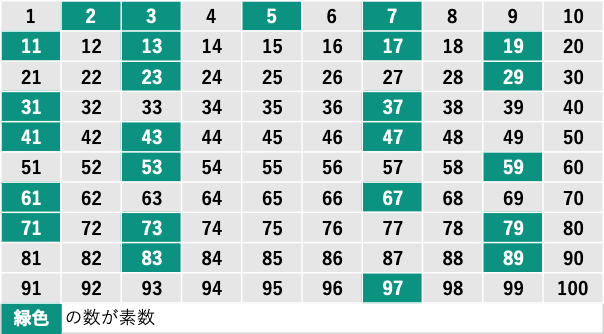
素数2こう.png
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
の25個が100までの素数です。
2, 3, 5, 7, 11, 13, 17, 19くらいまでは素数の問題を扱うときによく使うため暗記しておきましょう。

また、中学受験で難関中学を目指している場合は、100までの素数は一目で判別できる必要があります。
書き出す場合には25個であるということを注意すれば抜け漏れやミスが減ります。

なぜ1は素数ではないのか

ここで素数に1が含まれないことを不思議に思うかもしれませんが、1は素数ではありません。
1の場合は、1とその数(1)自身以外に約数が無いので素数のように思えますが、1は約数が1の1つのみ、素数は約数を2つ持つため、その違いから1は素数から外されています。
理由としてはこうですが、1は素数ではないと覚えてしまいましょう。

素数の判定方法

素数は無限にあり、暗記することは不可能です。ある数が素数かどうかを判定するにはどうすればよいでしょうか。
素数かどうかの判定方法は「割り切れる数を探す」ことです。
ここで割り切れる数を探すテクニックをいくつか紹介します。

2で割り切れることの確認（1の位が偶数）

112や2004など、下一桁が偶数の場合は数として偶数です。偶数の素数は2のみであり、2以外の偶数は2で割り切れるため素数ではないと言えます。

3で割り切れることの確認（すべての桁の数を足すと3で割り切れる）

123はすべての桁を足すと1+2+3=6となり3で割り切れます。
このようなすべての桁の数を足したものが3で割り切れる数は3で割り切れることがわかっています。

5で割り切れることの確認（1の位が0か5）

10や305など1の位が0や5の場合は5で割り切れます。

暗記している素数で割ってみる

上記のいずれのパターンでもない場合は小さい素数からいくつか割り算してみましょう。
2, 3, 5は既に試しているため、7, 11, 13, 17, 19で割り切れないか確認します。
大概の場合は7, 11, 13, 17, 19で割り切れないことまで確認したら素数ではないと判定できます。

判定したい数をnとすると $\sqrt{n}$ までのの素数で割れなかったら素数であるということがわかっています。確実に判定したい場合はそこまで確認するとよいでしょう。
101が素数かどうかを判定する場合10< $\sqrt{101}$ <11なので2,3,5,7で割り切れないことを確認すればよいということになります。

まとめ

いかがでしたでしょうか。
本記事では、素数について解説しました。

素数のルールや判定方法を理解するのは少し難しいかもしれませんが、例を用いて考えてみることでより簡単に理解できるようになるはずです。

中学校で習う素数ですが、大学入試の問題にも出てくるほど奥が深いです。まだまだ素数を用いた難しい問題があるので、気になった方はぜひご自身で検索してみてください。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

明光プラスで読みたい記事のテーマを募集

明光プラスでは読者の方のご期待に沿えるように読みたい記事のテーマを募集しています。ぜひ下のリンクからアンケートにお答えください。

読みたい記事のテーマをリクエストする

あわせて読みたい記事

三平方の定理（ピタゴラスの定理）とは？計算の仕方と証明をやさしく解説！

2025.07.04

もくじ三平方の定理(ピタゴラスの定理)とは？三平方の定理(ピタゴラスの定理)の応...
連立方程式は簡単！基本問題の解き方から文章題の解き方まで徹底解説します

2025.07.01

連立方程式は中学数学の重要単元で、多くの生徒がつまずいてしまうテーマです。つまずきやすい理由は一元方程式や分数、小数など、これまでに学んだ数学の内容が一挙に出てきて総合力が問われ、また、使う文字や...
因数分解はなぜ必要？因数分解の意味とやり方、公式を1から解説！

2025.06.10

中学3年生や高校の数学で学ぶ「文字と式」の単元で登場する因数分解は、高校数学の基礎となる重要な単元です。さらに、高校入試でも頻出の分野のため、早めに理解しておくことが大切です。共通因数や定数項など...