2025.07.07
微分とは?微分は○○です!定義・公式・使い方を解説

高校数学の教育課程で避けては通れない微分。苦手に感じていたり、つまずいたりしてしまう方も多いのではないでしょうか。
本記事では、微分とは何かという定義から、基本公式・実際の使い方・例題・応用までを、図解・グラフ付きでやさしく解説します。
「微分が苦手」「テスト前に復習したい」「導関数の計算方法を知りたい」という方にぴったりの内容です!
微分とは?意味とイメージをつかもう
微分とは簡単に言うとグラフのある点における傾きを求める方法です。
たとえば、一次関数$y=ax+b$において、$a$が傾きを表すことはご存知かもしれません。このとき、$x$が1増えたときに$y$がどれだけ増えるか(=変化の割合)が「傾き」です。
ただ、日常の出来事や実際のグラフはまっすぐな直線ばかりではありません。車の速度が信号や渋滞で変化するように、グラフの傾きも常に一定ではないのです。
この「その瞬間の変化の割合」を求めるのが微分の役割です。
微分の定義と公式の導き方
傾きは2点間の変化量の比で考えます。
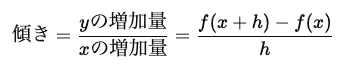
この時xの変化量(h)を限りなく0に近づけることで1点での傾きを求めることが微分です。
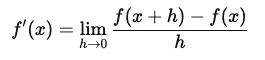
これが微分の定義です。ここで得られる$f'(x)$を導関数と呼びます。
実例から学ぶ微分〜車の速度〜
例えば次の40kmを1時間で走行した時の時間と走行距離を示したグラフからある瞬間の速度を計測することを考えます。
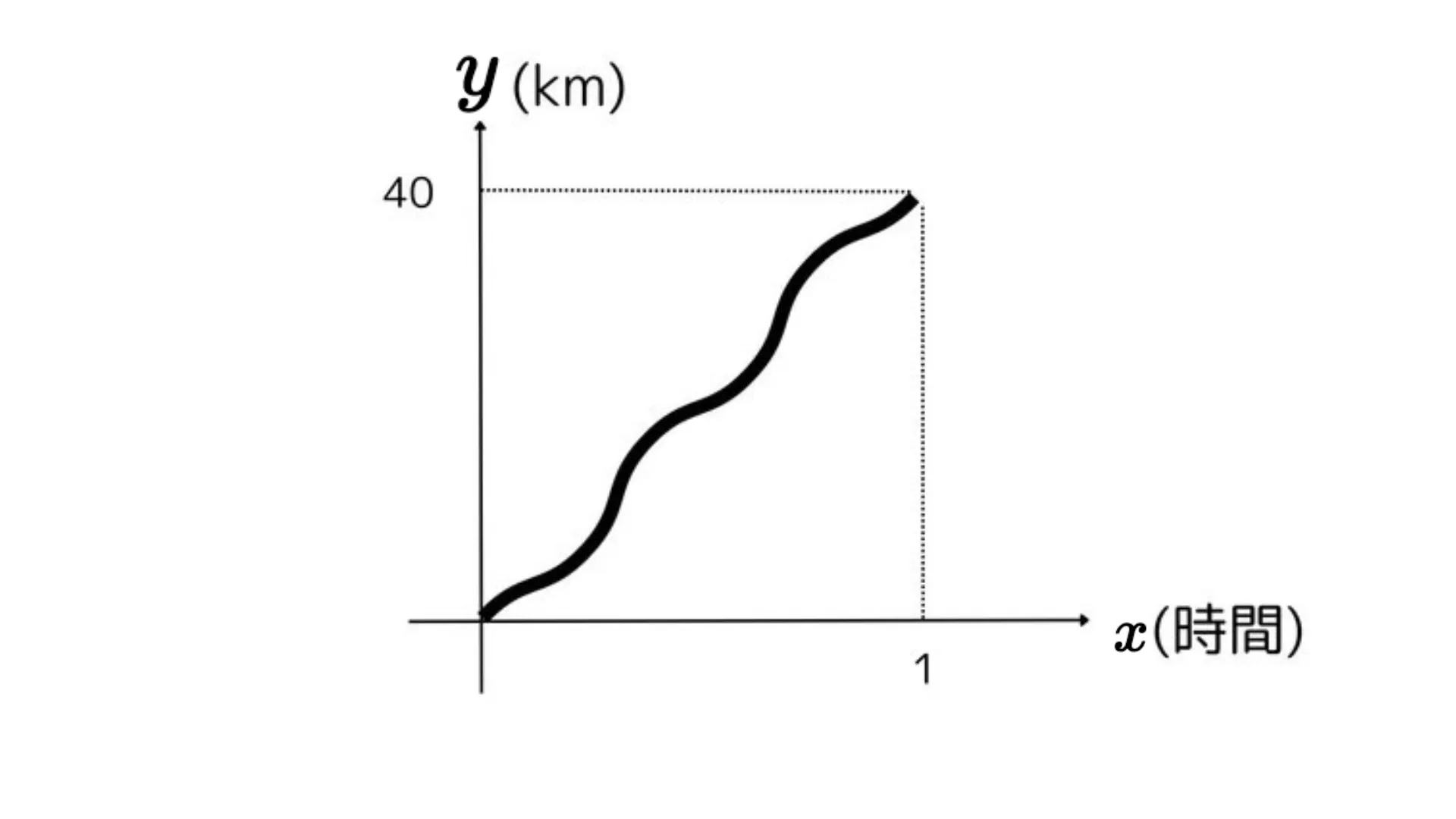
1時間の間、ずっと時速40kmで車が走行していた場合は、以下のグラフの赤い線で表せます。式で表すと、$x$が1(時間)進むと$y$が40(km)増えることになるので$y=40x$となります。
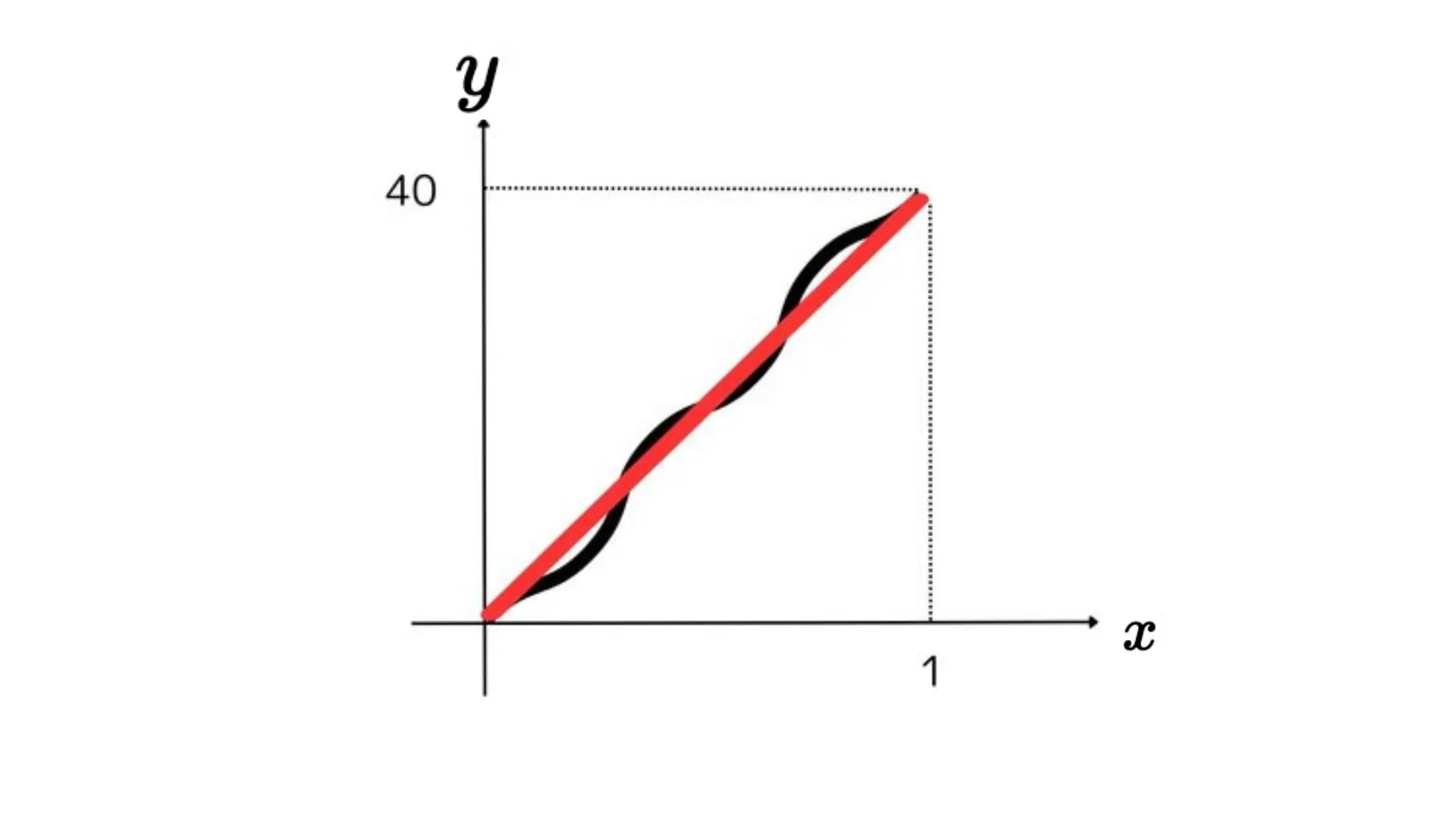
しかし実際には、高速に乗っていたり、赤信号で止まっていたりするので、その時々によって車のスピードメーターが示す速度は違うはずです。
微分ではその時々のスピードメーターの値、つまりグラフの傾きを求めることができます。例えば、この時の車の速度を求めてみましょう。
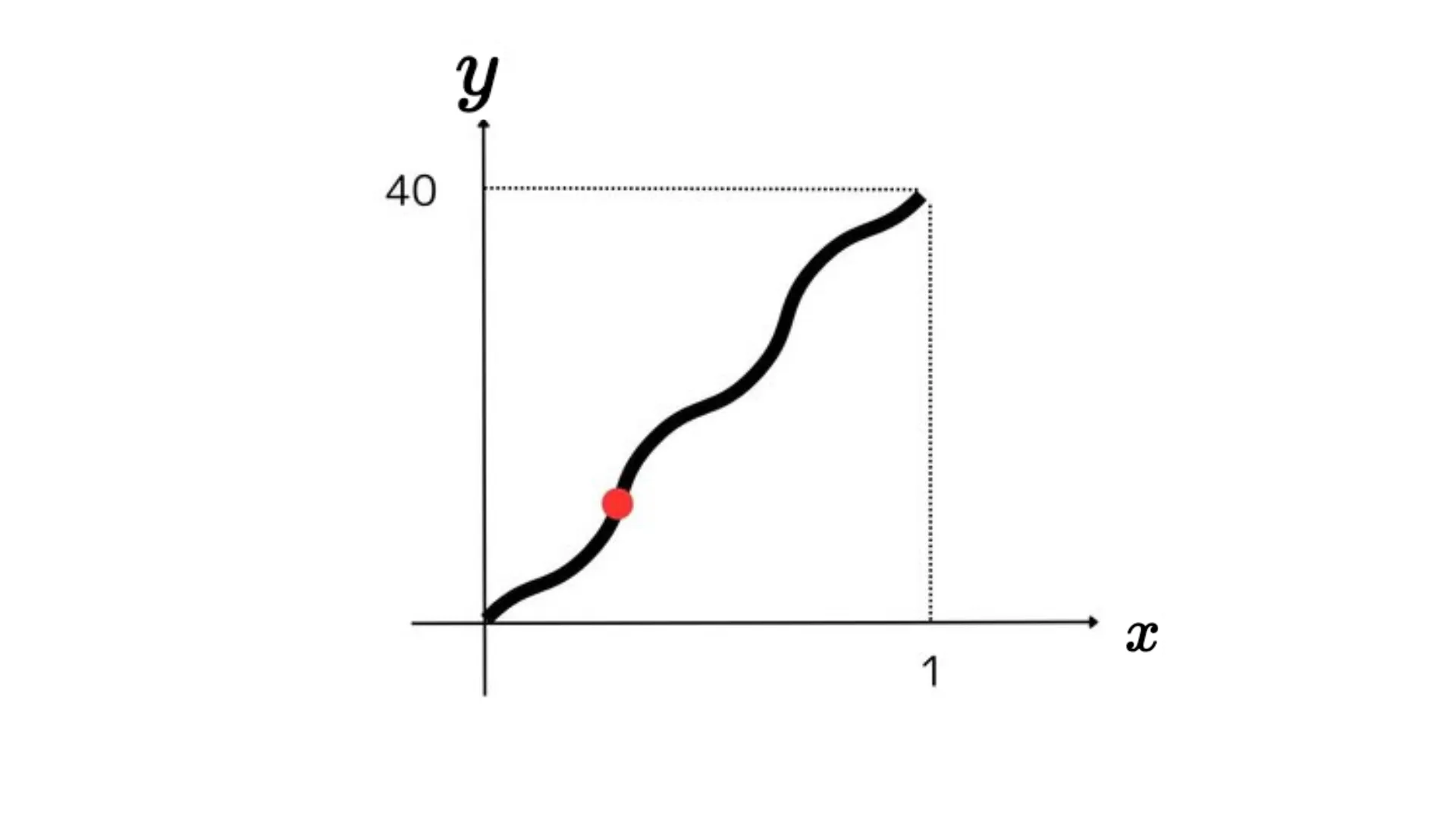
まず微分の導き方の考えで2点間の傾きを図示してみます。
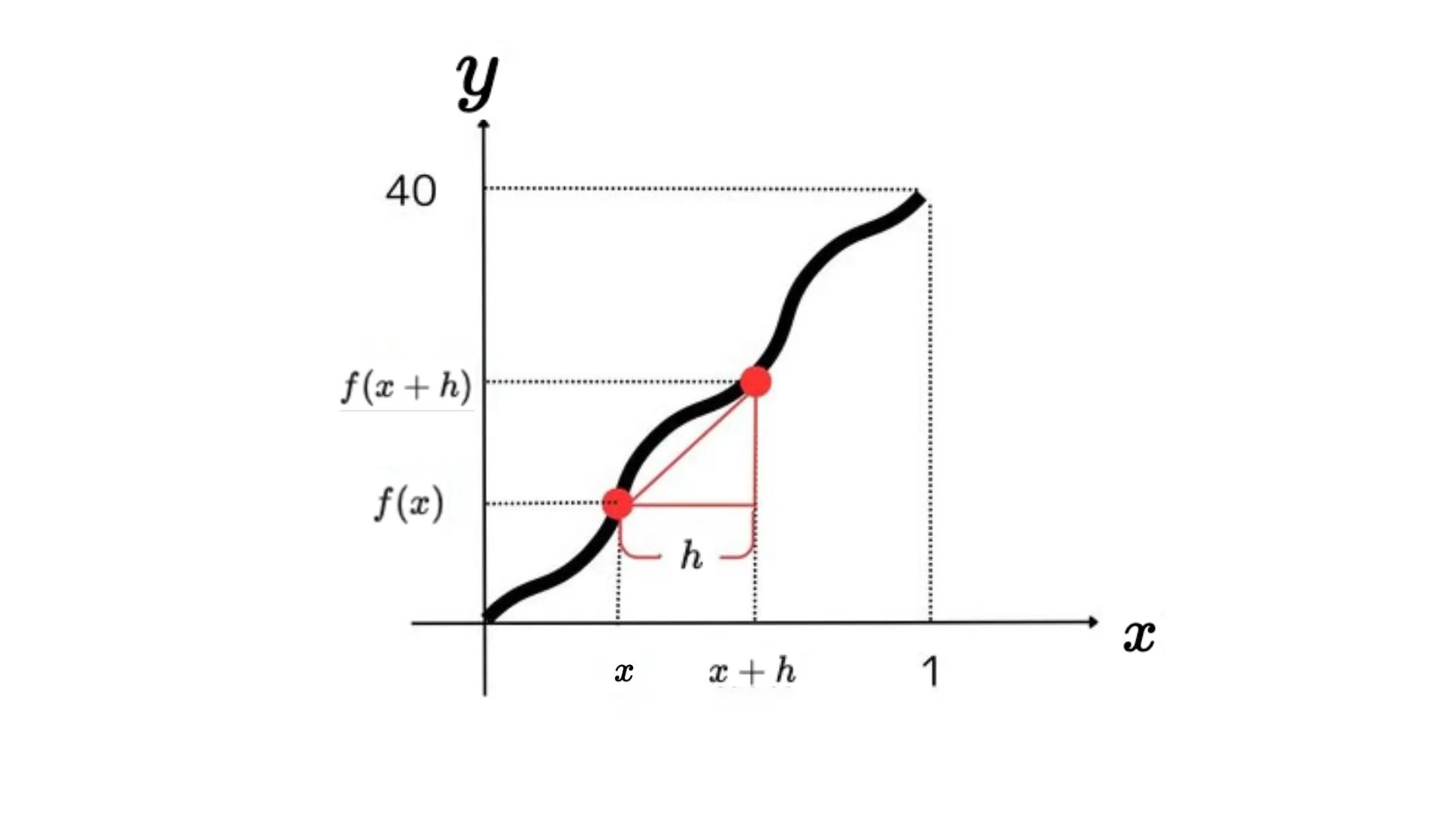
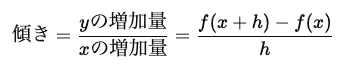
$x$の時点での傾きよりも緩やかに見えますね。これは$h$が大きいためです。
では$h$をもう少し小さい値にしてみましょう。
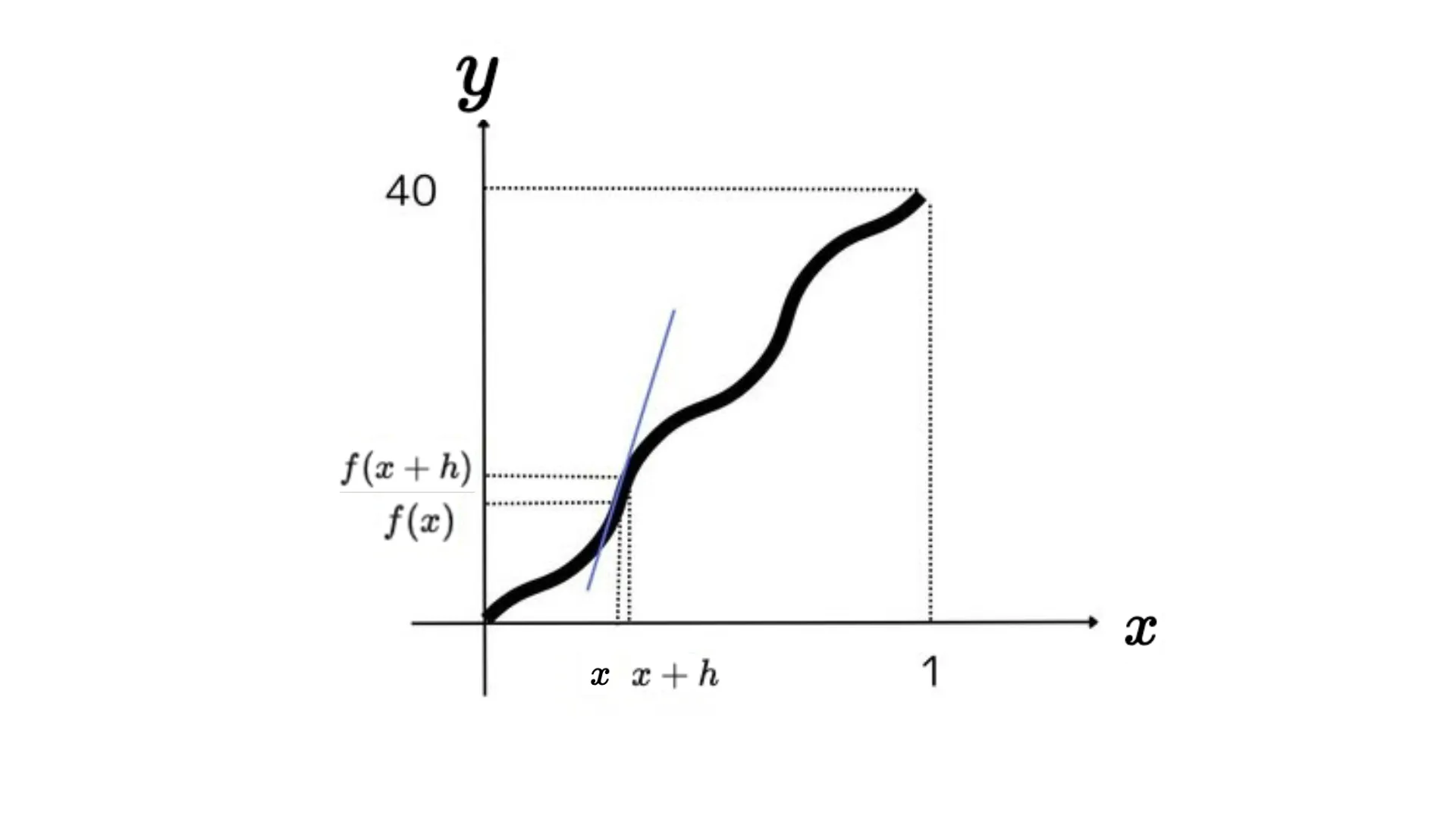
$x$の時点でのグラフの傾きと近くなってきました。その瞬間の速度を出すために、$h$の値を極限に小さくすることで、その瞬間の傾きを求めるのが微分の考え方です。
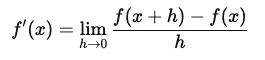
ここで先ほどの微分の定義の式をもう一度見てみましょう。
$f'(x)$は$f(x)$の導関数($f(x)$を微分したもの)、limは極限(limit)を表し、下にある$h→0$と合わせて、$h$を限りなく0に近づけるという意味です。そうするとこの式が表していることは$x$の時点での傾きを求めているということになります。
具体的な微分の導き方
では、$f(x)$が具体的な関数として表される時に、どのように計算すればよいのかを実際に確認していきましょう。
$f(x)$を微分して得られる関数を$f’(x)$とよく表し、導関数と呼びます。$f(x)=x^2$のときの導関数を求めてみましょう。
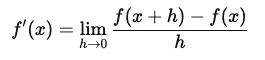
導関数の定義はこの式でしたので$f(x)=x^2$のとき、$x$にそれぞれ$x+h,x$を代入すると、$f’(x)$はこのようになります。
\[ \begin{align*} f'(x) &= \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} \\ &= \lim_{h \to 0} \frac{x^2 + 2xh + h^2 - x^2}{h} \\ &= \lim_{h \to 0} (2x + h) \end{align*} \]ここで、$h=0$に限りなく近づけると($h=0$を代入すると)$f’(x)=2x$と求まりました。
※なぜ$h$を限りなく0に近づける、という言い方をするのかと言うと、数学では0で割ることはご法度だからです。もともとの式では$h$が分母にあるため、$h=0$とすると0で割ってしまうことになります。計算上は$h$で約分をした後に、$h=0$を代入すると考えても問題ありません。
よく使う微分の公式(数学Ⅱ)
$(x^α)’=αx^{α-1}$
$α$がマイナス(分数)のときでも成り立ちます。$α$が正のときは、二項定理から導出することができます。
よく使う微分の公式(数学III)
三角関数の導関数(微分)
\[ \begin{align*} (\sin x)' &= \cos x \\ (\cos x)' &= -\sin x \\ (\tan x)' &= \frac{1}{\cos^2 x} \end{align*} \]指数・対数の導関数(微分)
\[ \begin{align*} (e^x)' &= e^x \\ (a^x)' &= a^x \log a \\ (\log x)' &= \frac{1}{x} \\ (\log_a x)' &= \frac{1}{x \log a} \end{align*} \]微分の基本的な演算
線形性:
\[
\begin{align*}
(af(x) + bg(x))' &= af'(x) + bg'(x)
\end{align*}
\]
積の微分:
\[
\begin{align*}
(f(x)g(x))' &= f'(x)g(x) + f(x)g'(x)
\end{align*}
\]
商の微分(分数の微分):
\[
\begin{align*}
\left( \frac{g(x)}{f(x)} \right)'
&= \frac{f(x)g'(x) - f'(x)g(x)}{f(x)^2}
\end{align*}
\]
特に、$g(x)=1$のとき、
\[
\begin{align*}
\left( \frac{1}{f(x)} \right)' &= -\frac{f'(x)}{f(x)^2}
\end{align*}
\]
合成関数の微分:
\[
\begin{align*}
\left\{ f(g(x)) \right\}' &= f'\left( g(x) \right) \cdot g'(x)
\end{align*}
\]
微分の使い方
ここまで微分の基礎を紹介しました。ここからは微分をすることで一体何ができるのか、その一部を紹介します。
微分で関数の増減・最大値・最小値がわかる!
微分を使うと、関数の傾き(増減)を調べることができます。
傾きがプラスなら関数は「増加」、マイナスなら「減少」、傾きが0になるところは、関数が増えるか減るかが切り替わるため、グラフの「山」や「谷」になるポイント(=極大や極小の候補)です。
その様子を視覚的にまとめたのが「増減表」と呼ばれるものです。
| x | … | −3 | … | 1 | … |
|---|---|---|---|---|---|
| f′(x) | + | 0 | − | 0 | + |
| f(x) | ↗ | 27 | ↘ | −5 | ↗ |
この表では、まず$導関数 f′(x)$を求め、その値が0になるxの位置(極大・極小の候補)を探します。その前後で傾きがプラスかマイナスかを確認すると、グラフが増えるのか減るのか、山なのか谷なのかがわかるのです。
たとえば、上の増減表では
・ $x=−3$までは傾きがプラス → 関数は増加
・ $x=−3$から$x=1$までは傾きがマイナス → 関数は減少
・ $x=1$以降は再び傾きがプラス → 関数は増加
このように、関数の形をグラフなしでもある程度イメージできます。
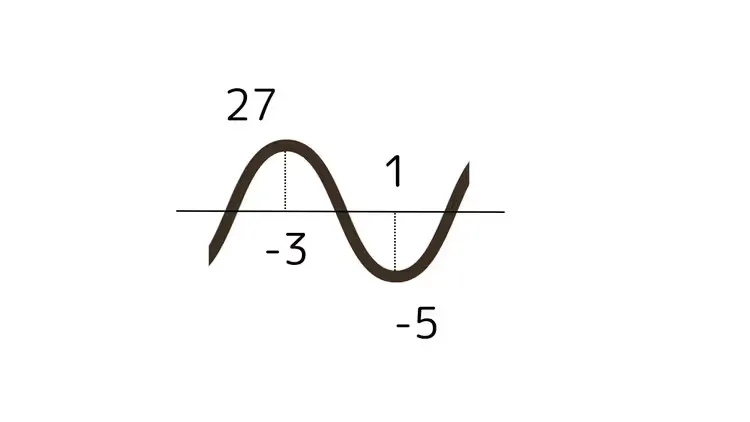
グラフの「山」になっている点が極大値、「谷」になっている点が極小値です。
最大値・最小値の見つけ方
関数の最大・最小を求めるには、以下の2つの候補を比べます:
1. 極大・極小の値(傾きが0になる点)
2. 範囲の端($x$の最小・最大)での関数の値
極大や極小は、関数の途中で一時的に最大・最小になる場所ですが、それ以外に最大・最小になり得るのが、定義された範囲の端($x$の最小値・最大値)です。そのため、求めた極値とあわせて端の値も調べて、一番大きい(または小さい)値がどこで出るかを比べる必要があります。
練習問題
$f(x) = x^3 - 6x^2 + 9x - 5 \quad (0 \leq x \leq 4) $
の最大値と最小値を求めよ
$f(x) = x^3 - 6x^2 + 9x - 5 \quad (0 \leq x \leq 4) $
の最大値と最小値を求めよ

曲線の接線と接点が求められる
微分を使うと、関数のある点における接線の方程式を求めることができます。
接線とは、曲線にぴったり接している直線で、その点での傾きが曲線と同じになるのが特徴です。
中学で習った一次関数では、傾きが$a$、点 ($x_0,y_0$)を通る直線の式は次のように表されました。
$y−y_0=a(x−x_0)$
この傾き$a$に当たる部分を、微分を使って求めると$ f′(x_0)$になります。つまり、関数$ f(x)$のグラフ上の点$x_0$における接線の式は、次のように表せます。
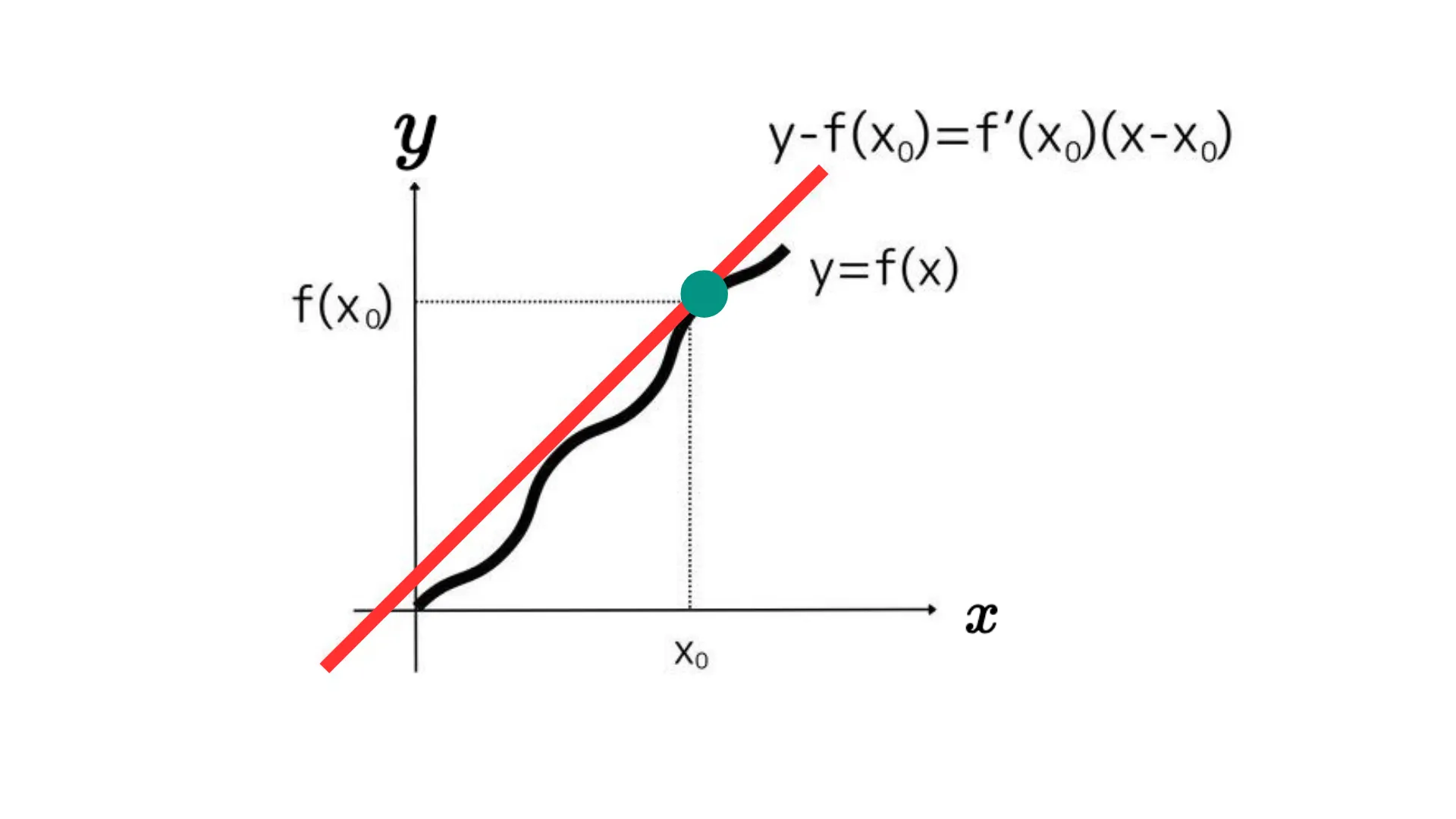
$y−f(x_0)=f′(x)(x−x_0)$
この公式を使えば、グラフのある点に引ける接線を簡単に計算で求められるようになります。
微分を使って「実数解の個数」を調べる
微分の知識は、方程式が実数解をいくつもつかを調べる問題にも応用できます。
例えば、方程式$x^2-2ax+4a-3=0$において、$a$が変化する場合、実数解の個数を$a$の範囲を用いて示せ、という問題があります。この場合、方程式を直線の方程式($x$の一次式と)とそれ以外に分けて考えます。
$f(x)=x^2$
$g(x)=2ax-4a+3$
元の方程式は$f(x)-g(x)=0$と表され、移項した$f(x)=g(x)$を求める、つまり$f(x)$と$g(x)$の交点の個数を求める問題になります。
$g(x)=2a(x-2)+3$と変形でき、(2,3)を通る傾き$2a$の直線だとわかります。
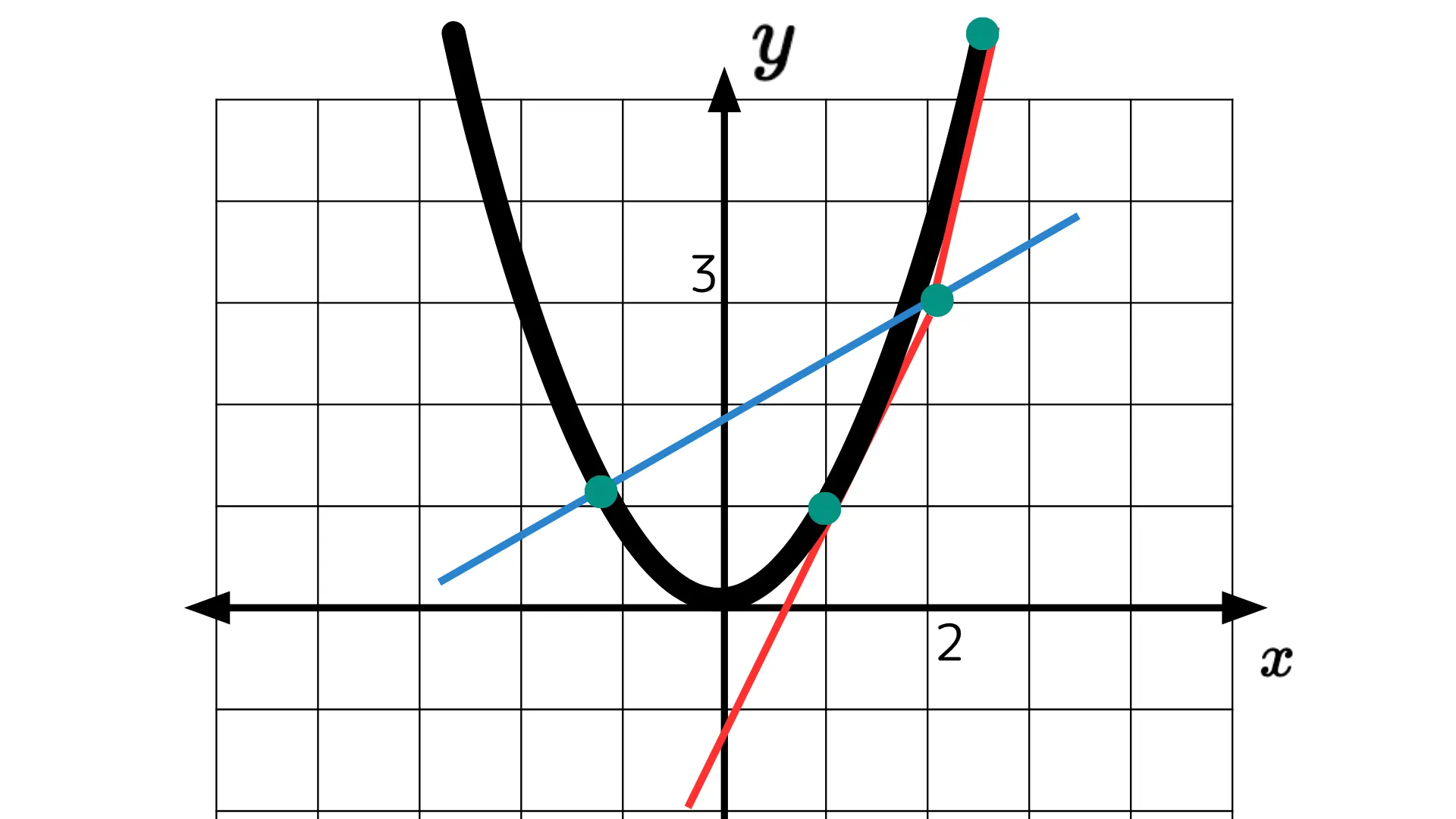
この図を見ればわかるように、$f(x)$とちょうど1点で接する場合に解(交点)が1つ、$f(x)$と$g(x)$が交わる場合に解(交点)が2つとなり、$f(x)$と$g(x)$が交わらない場合には解(交点)を持ちません。
・ちょうど1点で接する場合
まずは$f(x)$と$g(x)$が接する$a$の値を求めていきます。接するということは値と傾きが等しい点tがあるということなので
$f(t)=g(t)$・・・①
$f’(t)=g’(t)$・・・②
となります。
tを使って$f(t)=g(t)$, $f’(t)=g’(t)$の式をそれぞれ立てます。それぞれの導関数は
$f’(x) = 2x$
$g’(x) = 2a$
なので
$fx=a$となります。
これを①に代入して
$a^2=2a^2-4a+3$
$a^2-4a+3=0$
$(a-1)(1-3)=0$
$a=1,3$となりました。
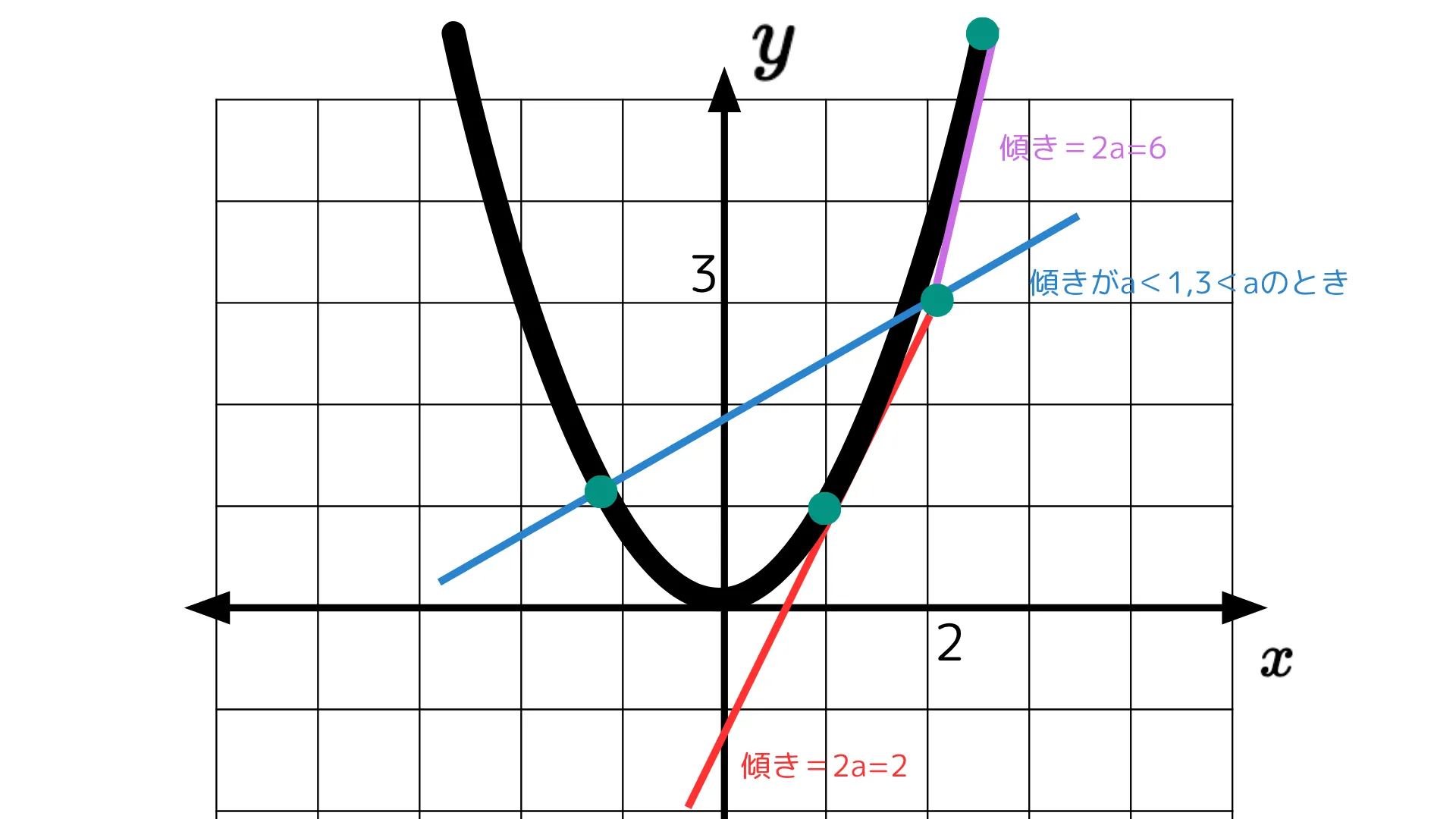
上の式より、
$a=1,3$のとき接するため、実数解1個
また、上のグラフからわかるように、$1<a<3$の範囲に$a$があるとき、直線が$f(x)$に接さないことがわかります。
よって、$1<a<3$のとき実数解0個
逆にこれ以外の範囲に$a$がある場合、$f(x)$と直線が交わることがわかります。
よって、$a<1,3<a$のとき実数解2個
以上のことから
$1<a<3$のとき実数解0個
$a=1,3$のとき実数解1個
$a<1,3<a$のとき実数解2個
となることがわかります。
このように、接点の条件を使って関数の実数解の個数を求める問題では、微分を使った「傾きの一致」がカギになります。
練習問題
$f(x)=3x^2-2x+1$の導関数$f'(x)$を求めなさい
$f(x)=3x^2-2x+1$の導関数$f'(x)$を求めなさい
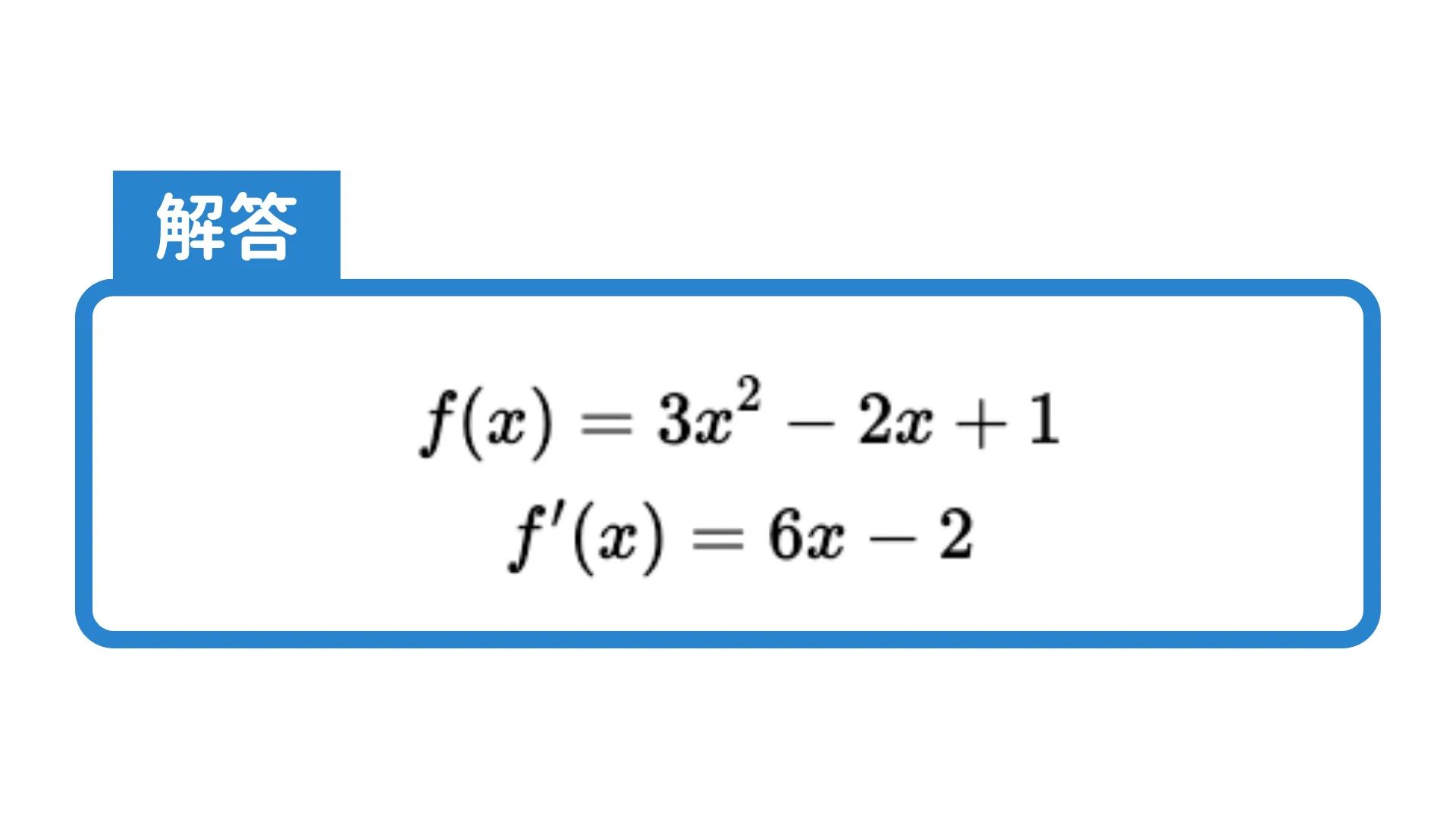
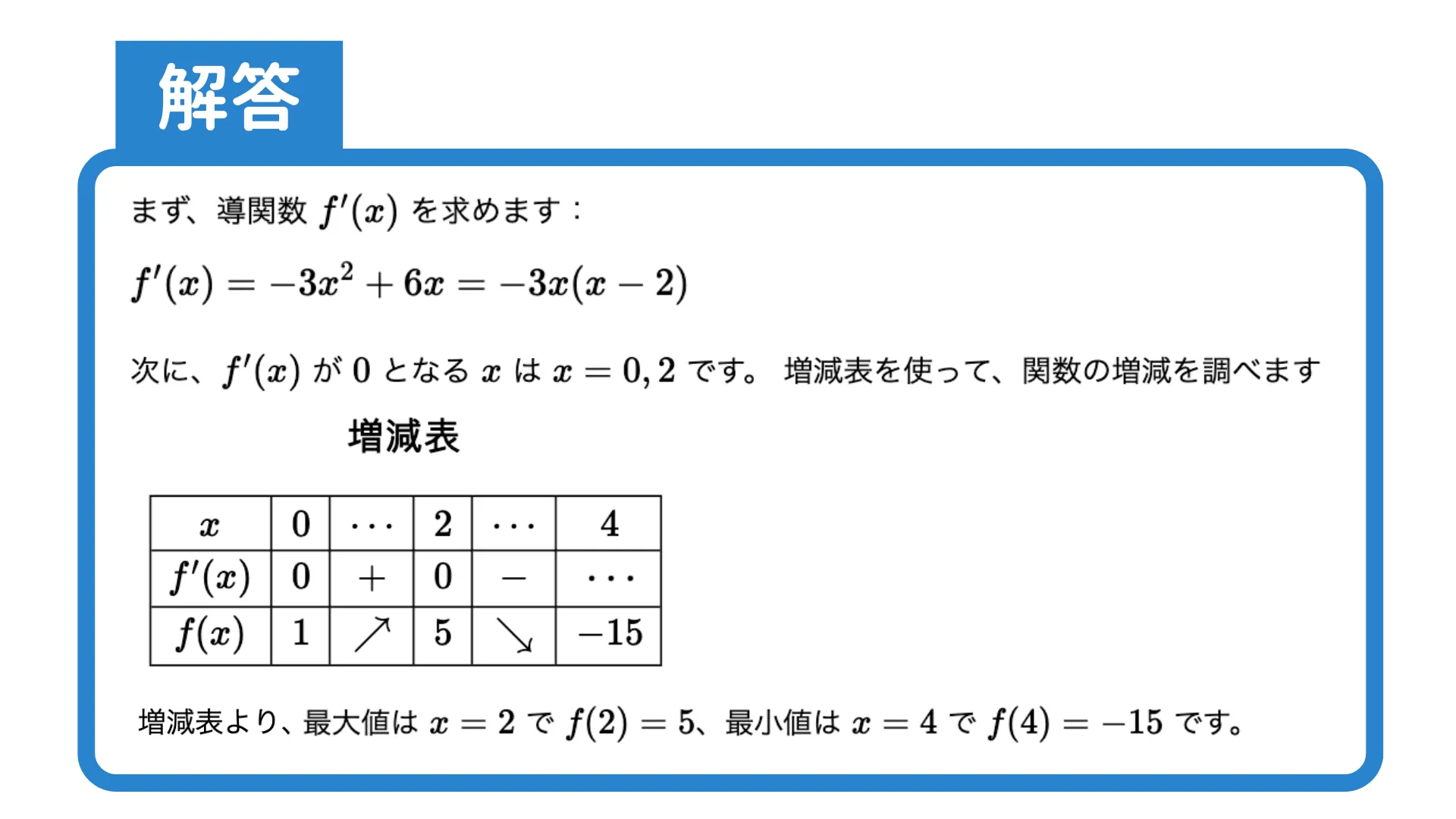
$f(x)=x^3-3x^2$の極大値・極小値を求めなさい
$f(x)=x^3-3x^2$の極大値・極小値を求めなさい

$f(x)=-x^3+3x^2+1$について、区間$0≤x≤4$における最大値・最小値を求めなさい
$f(x)=-x^3+3x^2+1$について、区間$0≤x≤4$における最大値・最小値を求めなさい
$f(x)=x^2$において点$x=1$における接線の方程式を求めなさい
$f(x)=x^2$において点$x=1$における接線の方程式を求めなさい

まとめ
微分とは、関数のその瞬間の変化の割合=傾きを求める方法です。
この記事では、微分の定義や基本公式、最大・最小の求め方、接線の公式など、必ず押さえておきたいポイントを一通り学んできました。
微分が使えるようになると、グラフの形を読み取ることができたり、実数解の個数を見極めたりできます。
この記事が微分への苦手意識を減らす助けとなれば幸いです。
教室数・生徒数No.1の個別指導塾!
明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。
お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。
この記事を家族や友人に教える
あわせて読みたい記事
-

三角関数(sin, cos, tan)入門!公式をわかりやすく覚える方法を紹介!
2025.06.26
三角関数では$\sin$(サイン),$\cos$(コサイン),$\tan$(タンジェント)や$\theta$(シータ)といった聞きなれない呪文のような言葉が多く出てくるのに加え、覚える公式が多いため...
-

三角比(sin, cos, tan)とは?覚え方と三角比の表も紹介!
2025.06.20
三角比ではsin(サイン),cos(コサイン),tan(タンジェント)やθ(シータ)といった聞きなれない呪文のような言葉がでてくるうえに、覚えることも多いため苦手意識を持っている方も多いのではないで...
-

等比数列は簡単!一般項や和の公式を1から解説します
2025.06.06
数Bの数列を学習すると等差数列の次に学ぶのが等比数列です。しかし等比数列に比べて見た目が複雑で規則性も掴みにくいため、苦手意識を持っている人も多いのではないでしょうか。等比数列は漸化式の問題を解くと...
タグ一覧
おすすめ記事
-

作文の書き方|小中学生向けにコツと例文+原稿用紙の正しい使い方をわかりやすく解説!
2025.07.03
作文が苦手という方は多いです。「何を書いていいかわからない」「うまく書けない」といった悩みの多くは、書き方のルールや型を知ることで解決できます。この記事では、作文の書き方を4つのステップでわかりやす...
-

【無料テンプレート付き】勉強計画の立て方|効率的な学習を実現する勉強計画表とは?
2025.07.03
「勉強しなきゃ」と思っても、いざ机に向かうと何から始めればいいかわからない…そんな経験はありませんか? 実は、成績アップに欠かせないのが“計画的な学習”です。 目標に向かって着実に前進するに...
-

【小論文の書き方】構成・テクニックを例文付きで解説!高校生向け完全ガイド
2025.06.26
「受験科目に小論文があるけれど、どうやって書けばよいかわからない」 というように、小論文に苦手意識をもつ高校生は多いのではないでしょうか。 小論文には書き方や構成の仕方...
-

自主学習のネタの決め方・ノートの書き方を解説!
2025.05.29
学校から自主学習をするようにと言われて、「何をすればいいの?」「進め方があってるのか不安」と悩まれているご家庭も多いことでしょう。 そこでこの記事では、そもそも自主学習をする目的、ネタの探し方・決め...
-

定期テスト(中間テスト・期末テスト)の勉強はいつから始める?高得点を狙える勉強法とは
2021.02.22
定期テストの勉強はいつから始めていますか?定期テストの結果は、1年の成績を大きく左右するうえ、内申にも直結します。そのため受験を視野に入れた勉強では、学力を高めることと同時に、定期テストで高...









