明光義塾へ
学習

2024.11.11     

【数学B】Σ(シグマ)の定義や使い方、公式と計算方法を1から解説！

シグマの公式_main.png

数学Bで学ぶ数列では、Σ(シグマ)という記号が登場します。計算方法がわからず、苦手に感じたり、暗記しようとしてつまずいたりする方も多いのではないでしょうか。この記事ではΣ(シグマ)の定義や使い方、覚えておくべき公式とその計算方法を1からやさしく解説します。

もくじ

Σ(シグマ)とは？

まずは、Σ(シグマ)という記号がどのようなものかを知りましょう。
Σ(シグマ)は、繰り返しの和を簡潔に表現するために使われる記号です。ギリシャ文字のΣはアルファベットのSに相当し、「sum（和）」に関連して和の記号として用いられています。

具体的な使い方を見てみましょう。
例えば、「1から100までの数をすべて足す」という式をそのまま書くと、
$1+2+3+...+100$
となり、…を省略せずに書くと、非常に長くなってしまいます。
しかし、Σを使うことで、簡潔に表現できます。


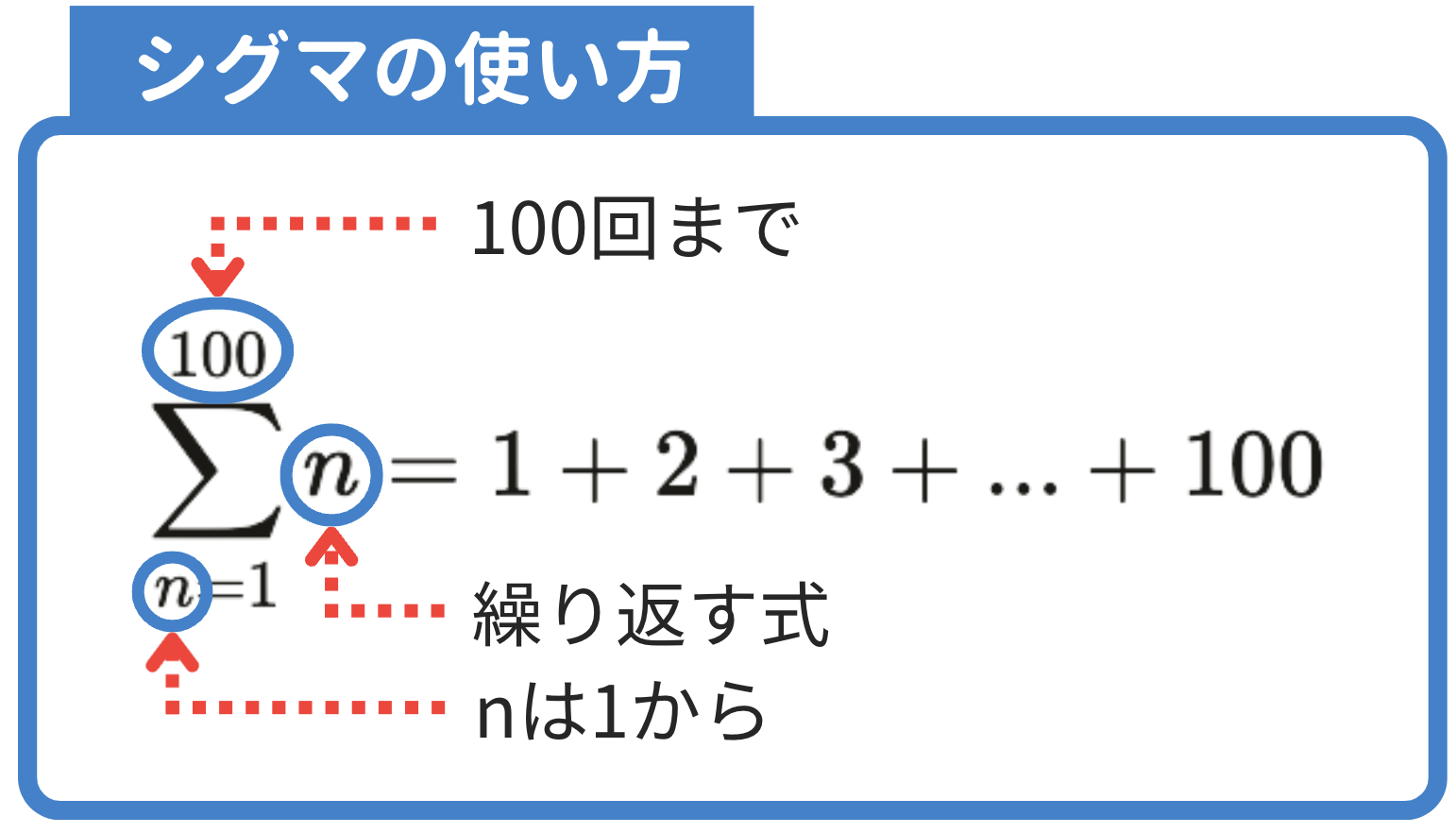
sigma1.png

このようにΣ(シグマ)を用いて、$\sum_{n=1}^{100} n$と書くことで、変数nが1から100まで繰り返される際の和を示します。

具体的なΣ(シグマ)のルールは、

・下の右辺に書いてある数字から
・上に書いてある数字まで1ずつ増やしていったときに
・右に書いてある式を繰り返し足していく

というものです。

余談ですが、情報Ⅰで学ぶ繰り返し処理とΣ（シグマ）には共通点があります。

繰り返し処理を学ぶ際に、Σ（シグマ）と関連づけると理解が深まるかもしれません。逆に、繰り返し処理を理解している場合は、Σ（シグマ）を理解する助けにもなるでしょう。

以下に$\sum_{k=1}^{100}k$を求めるJavaScriptのコードを示します。興味のある方は、ぜひ参考にしてみてください。

コードの表示 

let sum = 0;
for (let k = 1; k <= 100; k++) {
  sum += k;
} 
console.log(sum); // 5050が出力される

Σ(シグマ)の一般式

Σ(シグマ)の一般式は、次のように表されます。


sigma2.png

Σ(シグマ)は、右、下、上に記述された内容によって、どのような繰り返しの和であるかが決まります。それぞれの役割について詳しく説明します。

Σ(シグマ)の右

繰り返しの対象となる式を記述します。ここでは変数を使用でき、後述する「下」に書かれる変数と連動します。

Σ(シグマ)の下

「右」で使用する変数（使わない場合もあります）と、その初期値を記述します。多くの場合は1から始まりますが、必ずしもそうとは限りません。

Σ(シグマ)の性質

次に、Σ(シグマ)の計算で覚えておきたい、重要な性質について解説します。

sigma3.png

これらの性質は簡単に証明できます。

和の分離の証明

\begin{aligned} \sum_{k=1}^n\left(a_k+b_k\right) =&\left(a_1+b_1\right)+\left(a_2+b_2\right)+\cdots+\left(a_n+b_n\right) \\ =&\left(a_1+a_2+\cdots+a_n\right)+\left(b_1+b_2+\cdots+b_n\right) \\ =&\sum_{k=1}^n a_k+\sum_{k=1}^n b_k \end{aligned}

共通因数のくくり出しの証明

\begin{aligned} \sum_{k=1}^n p a_k &=p a_1+p a_2+\cdots+p a_n \\ & =p\left(a_1+a_2+\cdots+a_n\right) \\ & =p \sum_{k=1}^n a_k \end{aligned}

これら2つをまとめると、以下のようになります。合わせて導出できるようにしておきましょう。

$\sum_{k=1}^n\left(p a_k+q b_k\right)=p \sum_{k=1}^n a_k+q \sum_{k=1}^n b_k$

覚えておきたい5つのΣ(シグマ)の公式

ここで、覚えておきたい5つのΣ(シグマ)の公式を紹介します。
なお、これらの公式は、初期値が1の場合のみ使えることに注意してください。


シグマ_4.png

これらは導き出し方も合わせて理解して覚えておきましょう。

①定数項の和の導き方

まずは、定数項の和です。定数を繰り返し足すだけなので、簡単に導くことができます。


シグマ_5.png

②等差数列の和の導き方

次に等差数列の和です。


シグマ_6.png

等差数列の和は、同じ数列を逆順に並べて足し合わせ、その合計を2で割ることで求めることができます。例えば、1から19までの奇数の和は以下のようにして 100 と求めることができます。


シグマ_7.png

この性質を利用して、等差数列の和を導出してみましょう。


シグマ_8.png

③二乗の和の導き方

こちらは少し難解なため、公式を覚えておくだけでも十分です。


シグマ_9.png

次の式を利用して、
$(k+1)^3 = k^3 + 3k^2+3k+1$
以下の式が導き出せます。
$(k+1)^3 - k^3 =3k^2+3k+1$
これを利用します。


シグマ_10.png
シグマ_20_2.png

$\sum_{k=1}^n k=\frac{1}{2} n(n+1)$
$\sum_{k=1}^{n}1=n$
を代入して整理すると
$(n+1)^3-1^3=3 \sum_{k=1}^n k^2+3 \cdot \frac{1}{2} n(n+1)+n$

よって
\begin{aligned} 3 \sum_{k=1}^n k^2 & =(n+1)^3-1-\frac{3}{2} n(n+1)-n \\ & =n^3+3 n^2+3 n-\frac{3}{2} n^2-\frac{5}{2} n \\ & =n^3+\frac{3}{2} n^2+\frac{1}{2} n \\ & =\frac{1}{2} n\left(2 n^2+3 n+1\right) \\ & =\frac{1}{2} n(n+1)(2 n+1) \end{aligned}

以上より、$\sum_{k=1}^n k^2=\frac{1}{6} n(n+1)(2 n+1)$となります。

④三乗の和の導き方


シグマ_11.png

こちらも少し難解なため、公式を覚えておくだけでも十分です。

次の式を利用して、
$(k+1)^4 = k^4 + 4k^3+6k^2+4k+1$
以下の式が導き出せます。
$(k+1)^4 - k^4 = 4k^3+6k^2+4k+1$
これを利用します。

シグマ_12.png
シグマ_21.png

$\sum_{k=1}^n k^2=\frac{1}{6} n(n+1)(2 n+1)$
$\sum_{k=1}^n k=\frac{1}{2} n(n+1)$
$\sum_{k=1}^{n}1=n$
を代入して整理すると、
$(n+1)^4-1=4 \sum_{k=1}^n k^3+6 \cdot \frac{1}{6} n(n+1)(2 n+1)+4 \cdot \frac{1}{2} n(n+1)+n$

$\sum_{k=1}^n k^3$について解くと、
$\sum_{k=1}^n k^3=\left\{\frac{1}{2} n(n+1)\right\}^2$となります。

⑤等比数列の和の導き方


シグマ_13.png

等比数列の和は、元の数列から数列をr倍したものを引くことで求めることができます。
$S=\sum_{k=1}^{n}ar^{k-1}$とすると

シグマ_14.png

よってr≠1のとき
$S_n = \sum_{k=1}^{n} a r^{k-1} = \frac{a(1 - r^n)}{1 - r} = \frac{a(r^n - 1)}{r - 1}$
となります。

初期値が1ではないときのΣ(シグマ)の求め方


シグマ_15.png

これまで紹介した公式は、初期値が1の場合にのみ適用されます。そのため、初期値が1ではない場合には少し工夫が必要です。具体的には、Σ(シグマ)の差分で求めることができます。

シグマ_16.png

Σ(シグマ)の計算をするときは、初期値に気をつけるようにしましょう。

Σ(シグマ)を使った計算の練習問題

最後に、いくつかΣ(シグマ)を使った計算の練習問題を解いてみましょう。

1.$\sum_{k=1}^{n}(k^3+k^2+k+1)$

2.$\sum_{k=3}^{10}(2k+a)$

3.$\sum_{l=1}^{n}(2k+a)$

4.$\sum_{k=1}^{n-1}(3\cdot3^{k-1})$


解答はこちら

まとめ

本記事では、Σ(シグマ)の定義や使い方、覚えておくべき公式について解説しました。

Σ(シグマ)の計算は暗記が多いと感じるかもしれませんが、仕組みやパターンを理解することで、効率よく計算できます。

今回紹介した公式や計算方法が自然に使えるように、Σ(シグマ)に関する演習問題を繰り返し解いて、理解を深めていきましょう。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

この記事を家族や友人に教える

明光プラスで読みたい記事のテーマを募集

明光プラスでは読者の方のご期待に沿えるように読みたい記事のテーマを募集しています。ぜひ下のリンクからアンケートにお答えください。

読みたい記事のテーマをリクエストする

関連タグ

#数学 #高校生

あわせて読みたい記事

タグ一覧

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

Home > 明光プラス > 学習 > 【数学B】Σ(シグマ)の定義や使い方、公式と計算方法を1から解説！