明光義塾へ
学習

2024.11.29

球の体積・表面積の求め方！公式や覚え方、なぜそうなるかを徹底解説！

球の体積・表面積サムネ.png

球の体積と表面積の求め方は、中学1年生で習う時には公式を暗記するだけですが、高校生になると公式がなぜそうなるのかを積分を使って証明することができます。この記事では中学生向けに公式とその覚え方を、高校生向けに公式がなぜそうなるのかの証明をあわせて解説します。

もくじ

そもそも球とは？

球の定義を聞かれると思わず考え込んでしまう方も多いのではないでしょうか。いきなり球を考えるのは難しいので、考えやすい円の定義から確認しましょう。

円

円の定義は「平面上で、ある点から等距離にある点の集まり」です。
円を作図する道具にコンパスがありますが、コンパスでは中心に針を刺して、そこから等距離にある点の集まりとなる線が引けるようになっています。


球_1.png

この円の定義を踏まえて考えると、球の定義はどうなるでしょうか？

球

球の定義は「空間内で、ある点から等距離にある点の集まり」です。円では2次元の平面を考えていましたが、球では3次元の空間について考えています。


球_2.png

球の体積の公式と覚え方

球の体積の求め方は公式を使います。半径$r$の球の体積はこのようになります。


球_3.png

覚え方は語呂合わせを使って
身の上に心配あるの3乗
み(3)の上にし(4)んぱい($π$)ある($r$)の3乗
と覚えておきましょう。

体積なので単位は$m^3$(立法メートル)や$cm^3$(立法センチメートル)のように長さの3乗の単位になります。この公式の中で長さの単位を持つのは$r$だけなので単位を理解しておけば$r$が3乗であることがわかります。

球の表面積の公式と覚え方

球の表面積の求め方も公式を使います。半径rの球の表面積はこのようになります。

球_4.png

覚え方は語呂合わせを使って
心配あるある
し(4)んぱい($π$)あるある($r×r$)
と覚えておきましょう。

面積なので単位は$m^2$(平方メートル)や$cm^2$(平方センチメートル)のように長さの2乗の単位になります。この公式の中でも長さの単位を持つのは$r$だけなので単位を理解しておけば$r$は2乗であることがわかります。

【高校生向け】球の体積の公式を積分を使って証明

球の体積の公式を証明する方法はいくつかありますが、円の積み重ねで球ができるという一番わかりやすい考えを使って求めていきます。


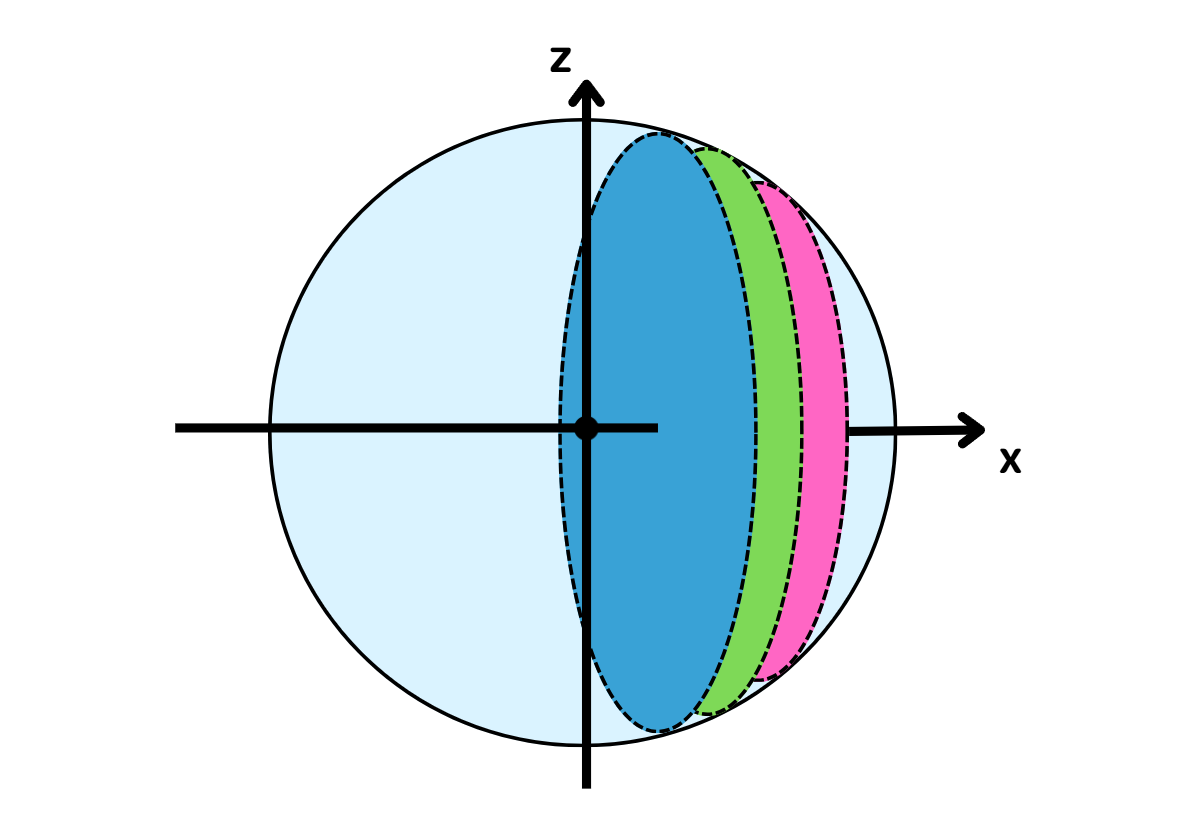
球_5.png

球の中心を原点において$x$軸と垂直な平面で輪切りにすることを考えます。このときにできる断面は$x$の座標によって半径が異なる円になります。
この輪切り1つ1つの幅を極限まで小さくしたときにできあがる、薄い円柱を積分することで球の体積を求めていきます。


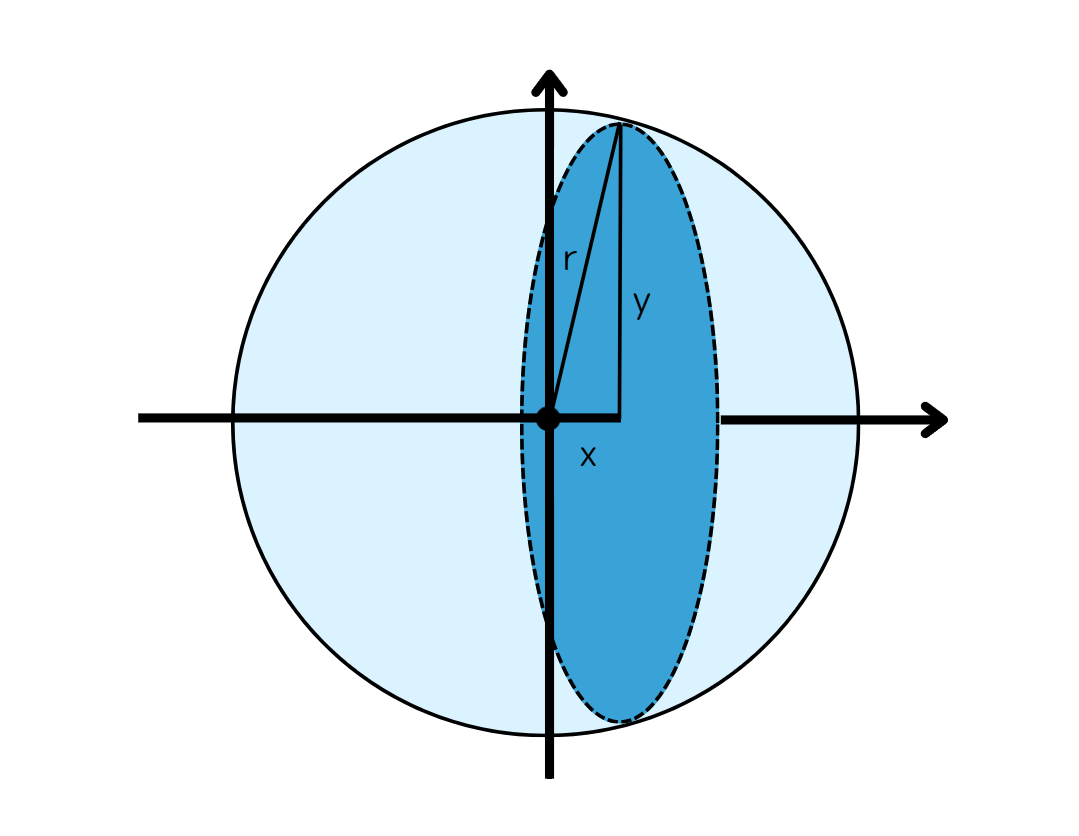
球_6.png

位置$x$での断面の円の面積は$\pi y^2$で、半径($y$)は円の方程式と三平方の定理からわかる通り
$x^2 + y^2 = r^2$
$y^2 = r^2 - x^2$
を満たします。
よって位置xでの円の面積は
$\pi y^2 = \pi(r^2-x^2)$
となり$dx$(極小の$x$)をかけることで薄い円柱の体積がわかります。

これを$-r≤x≤r$の範囲で積分すると球の体積が求まりますが、球は平面$x$=0($yz$平面)に対して対称なので、$0≤x≤r$の範囲で積分した値を2倍したものも球の体積になります。

よって球の体積は
$\int_{-r}^{r} \pi (r^2-x^2)dx = 2\pi\int_{0}^{r} (r^2-x^2)dx$
$=2\pi(r^3-\frac{r^3}{3})$
$=\frac{4}{3}\pi r^3$
となり公式が証明されました。


【高校生向け】球の表面積の公式を積分を使って証明


球の表面積の公式も証明の仕方はいくつかありますが、球の表面積を積分すると球の体積になることを利用して証明ができます。

球_7.png

図のように半径が$t$の薄い膜のようなものを考え、その表面積を$S(t)$と置きます。また、このような膜を球殻と呼びます。

球_8.png

この球殻を集めると球の体積を敷き詰めることができるため、表面積を$0≤t≤r$の範囲で積分すれば体積が求まります。
$\int_{0}^{r}S(t)dt = \frac{4}{3}\pi r^3$
この両辺をrで微分すると
$S(r) = 4\pi r^2$
となり、球の表面積が求められます。
球の表面積を積分すると球の体積になるということは、球の体積をrで微分すると球の表面積になると言い換えられます。この関係を理解しておくと公式も覚えやすくなります。

球の体積、表面積を求める練習問題

最後に、練習問題として下の図のような半径2cmの半球の体積と表面積を求めてみましょう。

球_9.png
　　　　

解答はこちら

まとめ

いかがでしたでしょうか。本記事では、球の体積と表面積の公式と、その公式の証明について解説しました。
中学生の皆さんは語呂合わせを使ったり、演習問題を繰り返し解いたりして公式を定着させましょう。
高校生の皆さんは積分の考え方を理解して、公式だけでなく証明までスムーズにできるように何度も復習してみましょう。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

この記事を家族や友人に教える

関連タグ

#中学生 #数学 #高校生

あわせて読みたい記事

タグ一覧

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

Home > 明光プラス > 学習 > 球の体積・表面積の求め方！公式や覚え方、なぜそうなるかを徹底解説！