2024.06.11
部分積分は〇〇を理解すれば簡単!なぜ必要なのか、導出も解説します

部分積分は数学Ⅲで出てきますが、苦手に感じていたり、つまずいたりしてしまう方も多いのではないでしょうか。本記事では、部分積分の必要性と公式の証明、そして部分積分のパターンについて解説していきます。
(※本記事では不定積分の形で紹介しますが、定積分でも同様に計算することができます。)
部分積分のやり方とその必要性
部分積分は、積の形で表される関数を積分する際に使用されます。一般的に、関数の積を直接積分することは難しいため、積分が可能な形に変形するための手法として部分積分が登場しました。

この公式はすらすらと書ける・言えるようにしっかり覚えましょう。計算の途中で公式を思い出すのに時間がかかってしまうと、部分積分を何度も使う問題では特に、かなりの時間をロスしてしまいます。また、公式を思い出すための労力が計算ミスを引き起こす原因にもなりかねません。
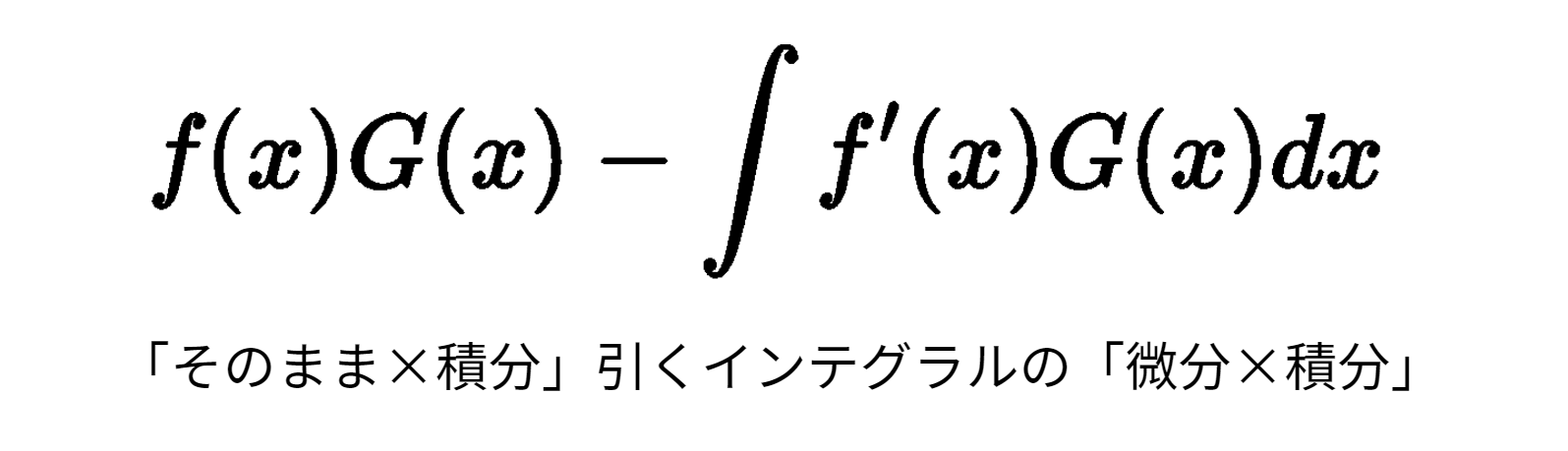
部分積分の式変形は、「そのまま×積分」引くインテグラルの「微分×積分」と覚えてしまいましょう。
部分積分公式の証明
ここで部分積分がなぜ成り立つのかを解説します。
部分関分は積の微分の公式から導出できます。積の微分の公式は以下の通りです。
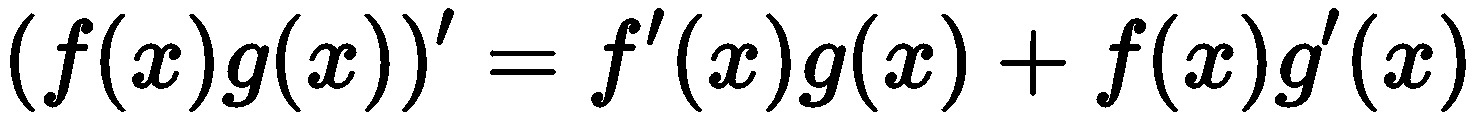
積の微分の公式の両辺を積分し、整理すると、
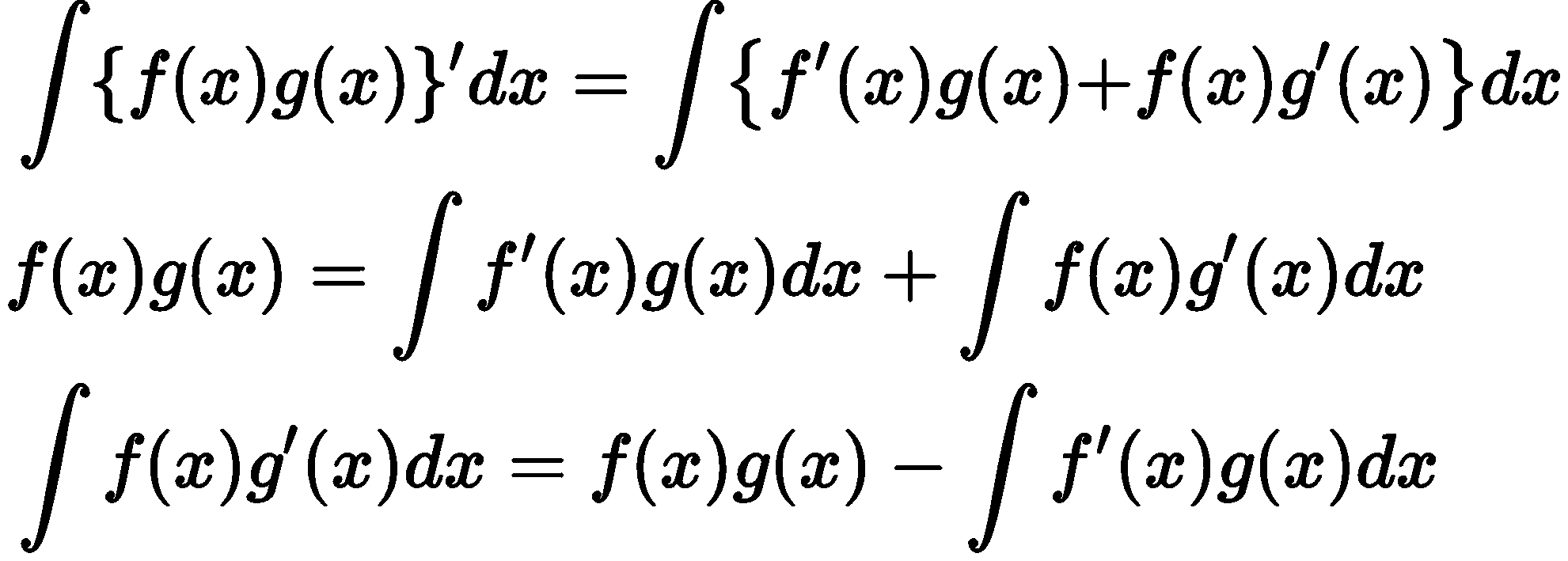
$g’(x)$を積分したものが$g(x)$なので部分積分の公式と同等のものが導出できました。
部分積分はパターンを理解すれば簡単!
一見すると項が増えてより複雑になっているように見えますが、各要素を一つ一つ見ていくことで部分積分のメリットが明らかになります。
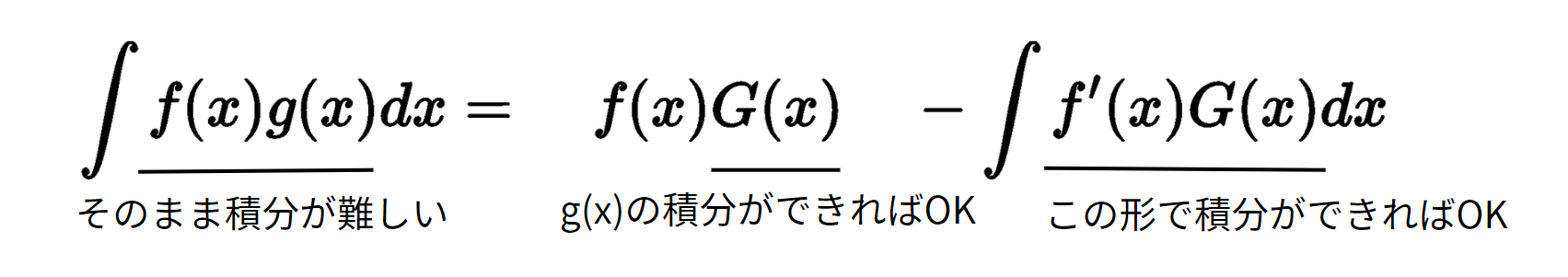
そのまま積分することが難しい関数を
①単体で積分のしやすい$g(x)$
②積分しやすい$f’(x)G(x)$の形
となるように$f(x)$と$g(x)$の積に分けるのが部分積分です。
そのため、関数を分解する際には、この2点を意識することが重要です。
しかし、積分しやすい$g(x)$や$f’(x)G(x)$を意識して分解するのは難しく、またすべての関数が部分積分で解けるわけでもありません。
高校数学で出てくる部分積分の問題は、ある程度パターンが決まっているため、それらを覚えることが重要です。部分積分をするメリットがある関数は、主に以下の3つのパターンです。
①$f’(x)$が定数になる
②$f’(x)G(x)$が約分できる
③計算結果として元々の関数が再び現れる
これらのパターンが適応できるように$f(x)$と$g(x)$を選ぶ必要があることを理解しておきましょう。それぞれの場合について詳しく解説していきます。
①$f’(x)$が定数になるパターン
$f’(x)$が定数になるものとして代表的なのは一次関数です。
例えば、\( xe^x \)を積分することを考えます。
$\int e^xdx = e^x$、$(x)'=1$であるため、
$f(x)=x, g(x)=e^x$として公式に当てはめると
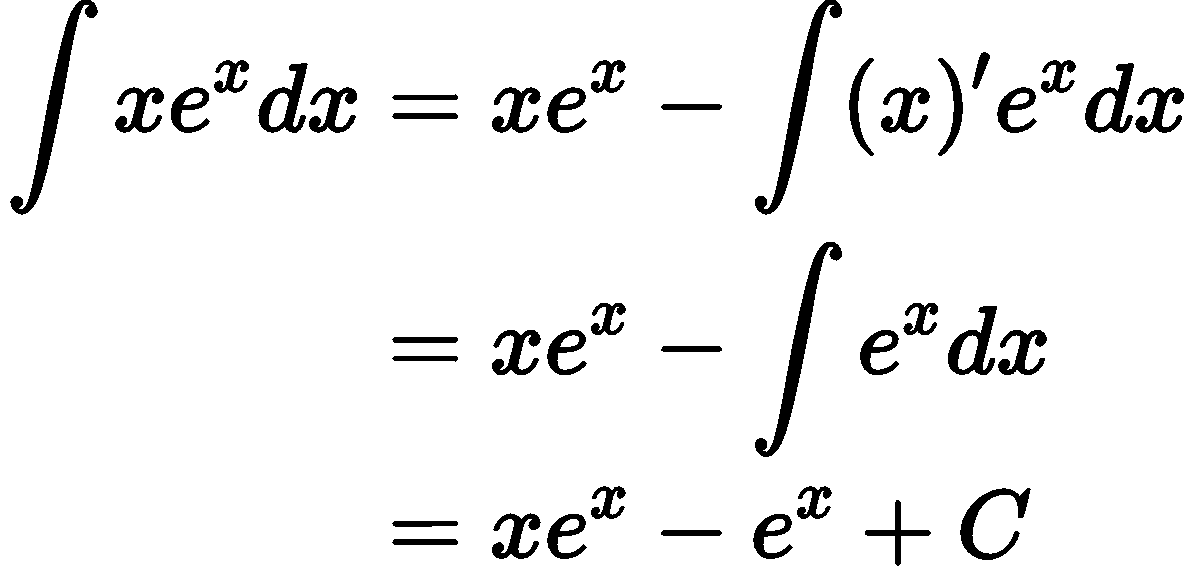
となります。(Cは積分定数)
$e^x$は積分しても形が変わらないため$g(x)$として使われることが多いです。覚えておきましょう。
また、1回の部分積分で計算できなくても、微分を繰り返すことで次数が下がる場合は部分積分できる場合があります。
例えば$x^2e^x$の$x^2$を$f(x)$、$e^x$を$g(x)$とし、部分積分を繰り返すと、$x^2e^x$の積分を計算することができます。
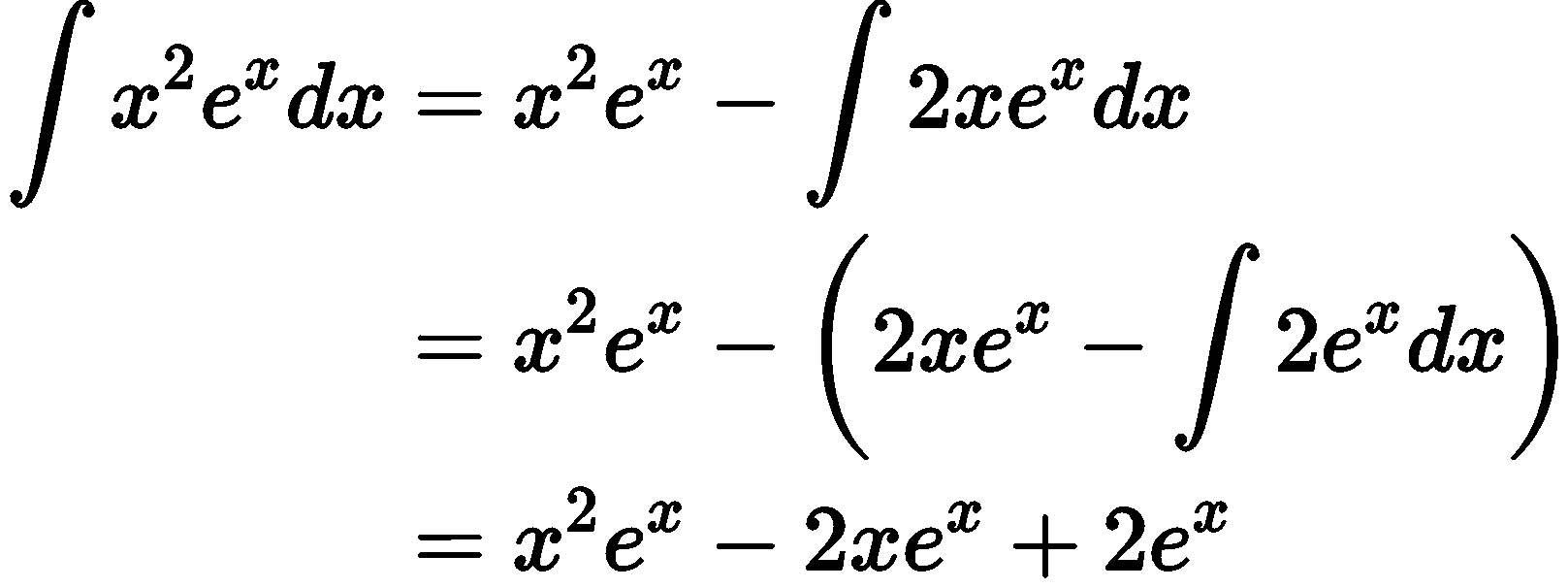
同様に、$f(x)$が任意のxの多項式、$g(x)$が$e^x$の場合は部分積分で計算が可能です。
部分積分を繰り返したときに$f(x)$と$g(x)$がどうなるかを想像し、繰り返しの部分積分で計算可能になるかどうかを見極めましょう。
②$f’(x)G(x)$が約分できるパターン
$f’(x)G(x)$が約分できるパターンとして頻出なのは、$(logx)'=\frac{1}{x}$となる$logx$を使う式です。
$xlogx$を積分することを考えます。
$f(x)=log(x),g(x)=x$として公式に当てはめると
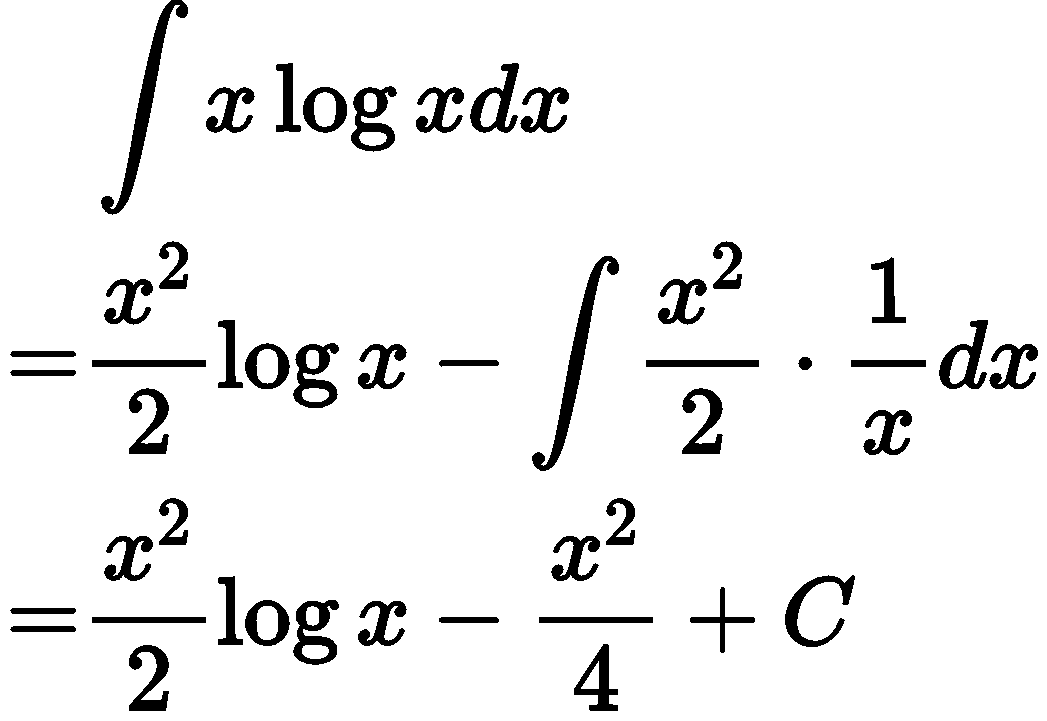
となります。積分の問題で$log$が出てきた場合は、まず$log$を$f(x)$として部分積分が適応できないかを考えてみましょう。
③計算結果として元々の関数が再び現れるパターン
部分積分を1回以上行うことで、もともとの関数と同じ形の式が生じることがあります。これを同形出現と言います。代表的な例は、$sinx$や$cosx$が含まれる関数です。これらの関数は2回微分することでもともとの$sinx$や$cosx$の形が出てきます。
同形出現のパターンでは、積分の形をうまく消去できる場合があります。
例えば、$e^xsinx$を積分することを考えてみましょう。
もとの積分を$I$とし、$f(x)=sinx,g(x)=e^x$として部分積分の公式に当てはめてみます。

このようにもともとの関数の積分の形が出現することで、積分の形を消去し、計算が可能になることがあります。$sinx$や$cosx$が含まれる積分の問題が出てきたときは、同形出現の部分積分を思い出すようにしましょう。
まとめ
いかがでしたでしょうか。
本記事では、部分積分の必要性と証明、部分積分のパターンについて解説しました。
$log$や三角関数を含む積分を自力で解くことは困難なため、部分積分の公式だけでなく、3つの頻出パターンも合わせて覚えておく必要があります。
公式や今回紹介したパターンがスラスラ出てくるようになるまで、部分積分の演習問題を繰り返し解くようにしましょう。
教室数・生徒数No.1の個別指導塾!
明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。
お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。
この記事を家族や友人に教える
あわせて読みたい記事
-

微分とは?微分は○○です!定義・公式・使い方を解説
2025.07.07
高校数学の教育課程で避けては通れない微分。苦手に感じていたり、つまずいたりしてしまう方も多いのではないでしょうか。 本記事では、微分とは何かという定義から、基本公式・実際の使い方・例題・応用までを、...
-

三角関数(sin, cos, tan)入門!公式をわかりやすく覚える方法を紹介!
2025.06.26
三角関数では$\sin$(サイン),$\cos$(コサイン),$\tan$(タンジェント)や$\theta$(シータ)といった聞きなれない呪文のような言葉が多く出てくるのに加え、覚える公式が多いため...
-

三角比(sin, cos, tan)とは?覚え方と三角比の表も紹介!
2025.06.20
三角比ではsin(サイン),cos(コサイン),tan(タンジェント)やθ(シータ)といった聞きなれない呪文のような言葉がでてくるうえに、覚えることも多いため苦手意識を持っている方も多いのではないで...
タグ一覧
おすすめ記事
-

作文の書き方|小中学生向けにコツと例文+原稿用紙の正しい使い方をわかりやすく解説!
2025.07.03
作文が苦手という方は多いです。「何を書いていいかわからない」「うまく書けない」といった悩みの多くは、書き方のルールや型を知ることで解決できます。この記事では、作文の書き方を4つのステップでわかりやす...
-

【無料テンプレート付き】勉強計画の立て方|効率的な学習を実現する勉強計画表とは?
2025.07.03
「勉強しなきゃ」と思っても、いざ机に向かうと何から始めればいいかわからない…そんな経験はありませんか? 実は、成績アップに欠かせないのが“計画的な学習”です。 目標に向かって着実に前進するに...
-

【小論文の書き方】構成・テクニックを例文付きで解説!高校生向け完全ガイド
2025.06.26
「受験科目に小論文があるけれど、どうやって書けばよいかわからない」 というように、小論文に苦手意識をもつ高校生は多いのではないでしょうか。 小論文には書き方や構成の仕方...
-

自主学習のネタの決め方・ノートの書き方を解説!
2025.05.29
学校から自主学習をするようにと言われて、「何をすればいいの?」「進め方があってるのか不安」と悩まれているご家庭も多いことでしょう。 そこでこの記事では、そもそも自主学習をする目的、ネタの探し方・決め...
-

定期テスト(中間テスト・期末テスト)の勉強はいつから始める?高得点を狙える勉強法とは
2021.02.22
定期テストの勉強はいつから始めていますか?定期テストの結果は、1年の成績を大きく左右するうえ、内申にも直結します。そのため受験を視野に入れた勉強では、学力を高めることと同時に、定期テストで高...









