明光義塾へ
学習

2025.06.04     

三角形の面積の求め方！学齢に応じた公式の一覧となぜそうなるのかを解説します

三角形の面積サムネ.png

三角形の面積を求める問題は小学生から習いますが、大学入試に至るまでいろいろな求め方を習います。場合によって使い分ける必要がありますが、全てを完全に理解している方は少ないのではないでしょうか。
本記事では小学生から高校生で習う三角形の面積の求め方を1からやさしく解説します。

もくじ

【小学生向け】底辺と高さがわかっている場合

まず最初に習う三角形の面積の求め方として「底辺×高さ÷2」があります。
三角形の面積2.png
なぜこの式で面積が求められるのか図で理解していきましょう。
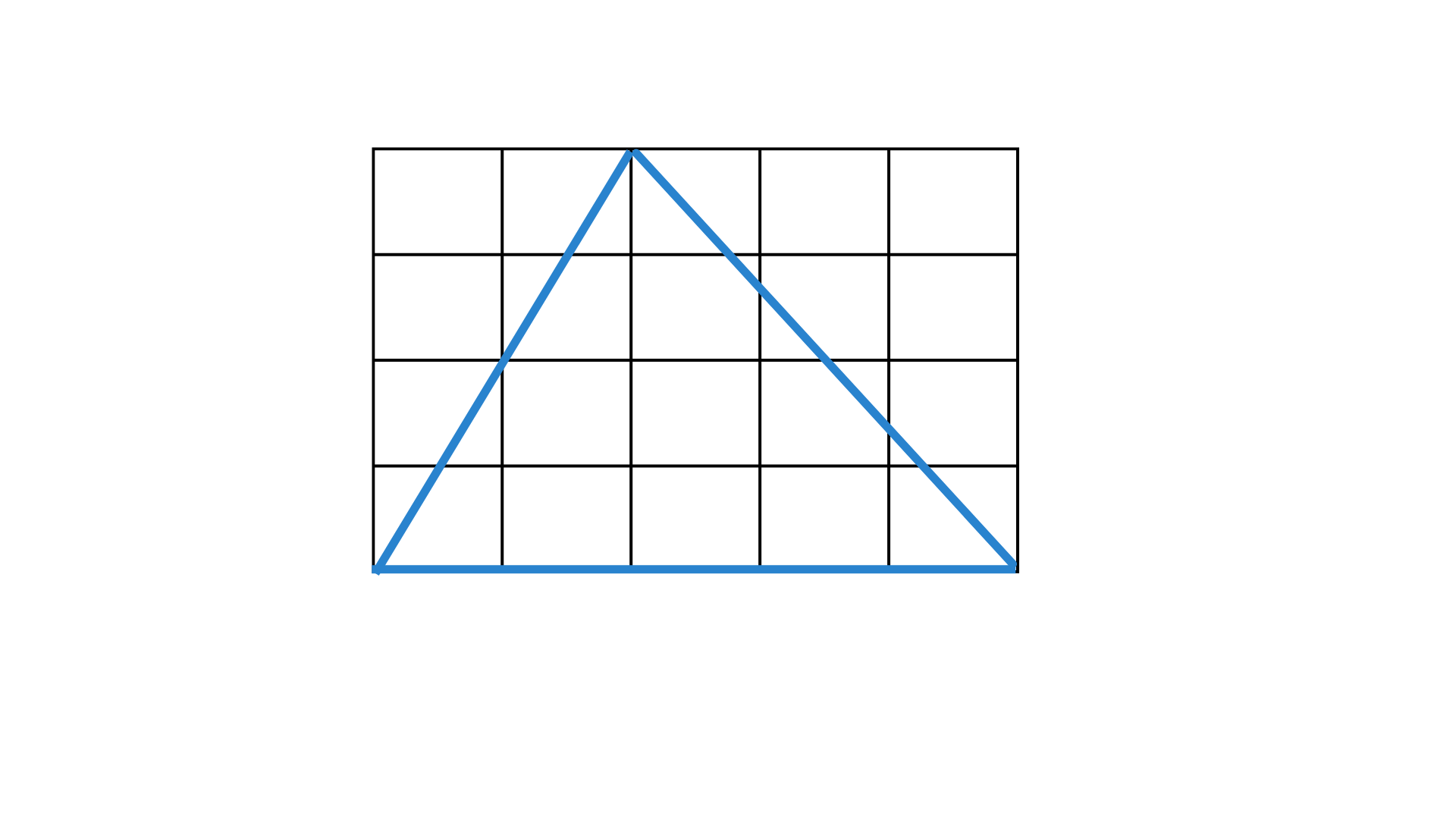明光プラス_球の体積・表面積_解答 (1).png 青い線で描かれた三角形の面積を考えるときに、このように色分けして考えてみます。
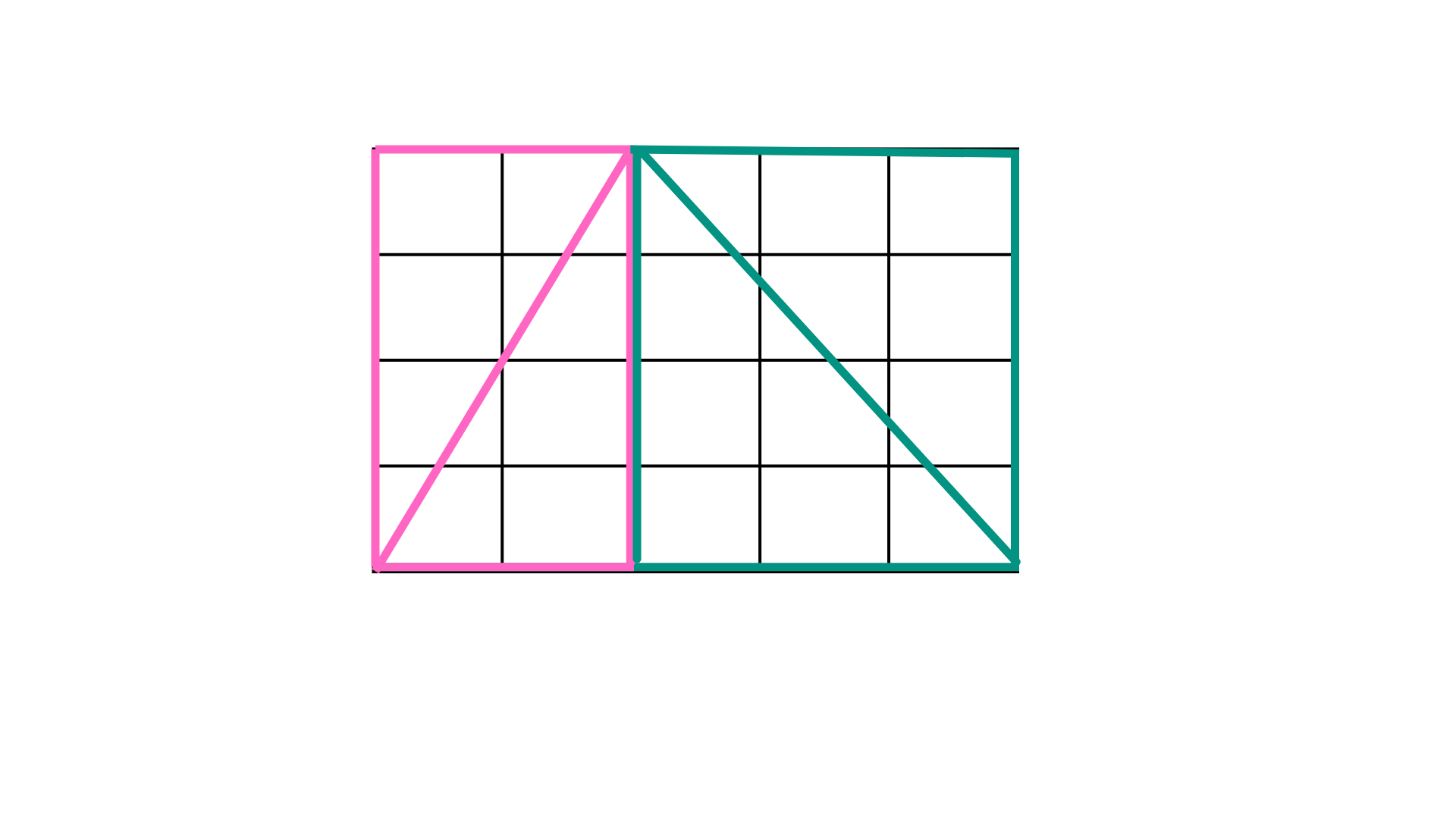
三角形の面積4.png
すると三角形の面積はピンクの四角形の半分と緑の四角形の半分の合計だとわかります。
つまり、三角形の面積はこの全体の四角形の面積の半分だと言えるため、
三角形の面積＝縦×横÷2
　　　　　　＝底辺×高さ÷2
ということがわかります。

また、平行四辺形を作って理解する方法もあります。
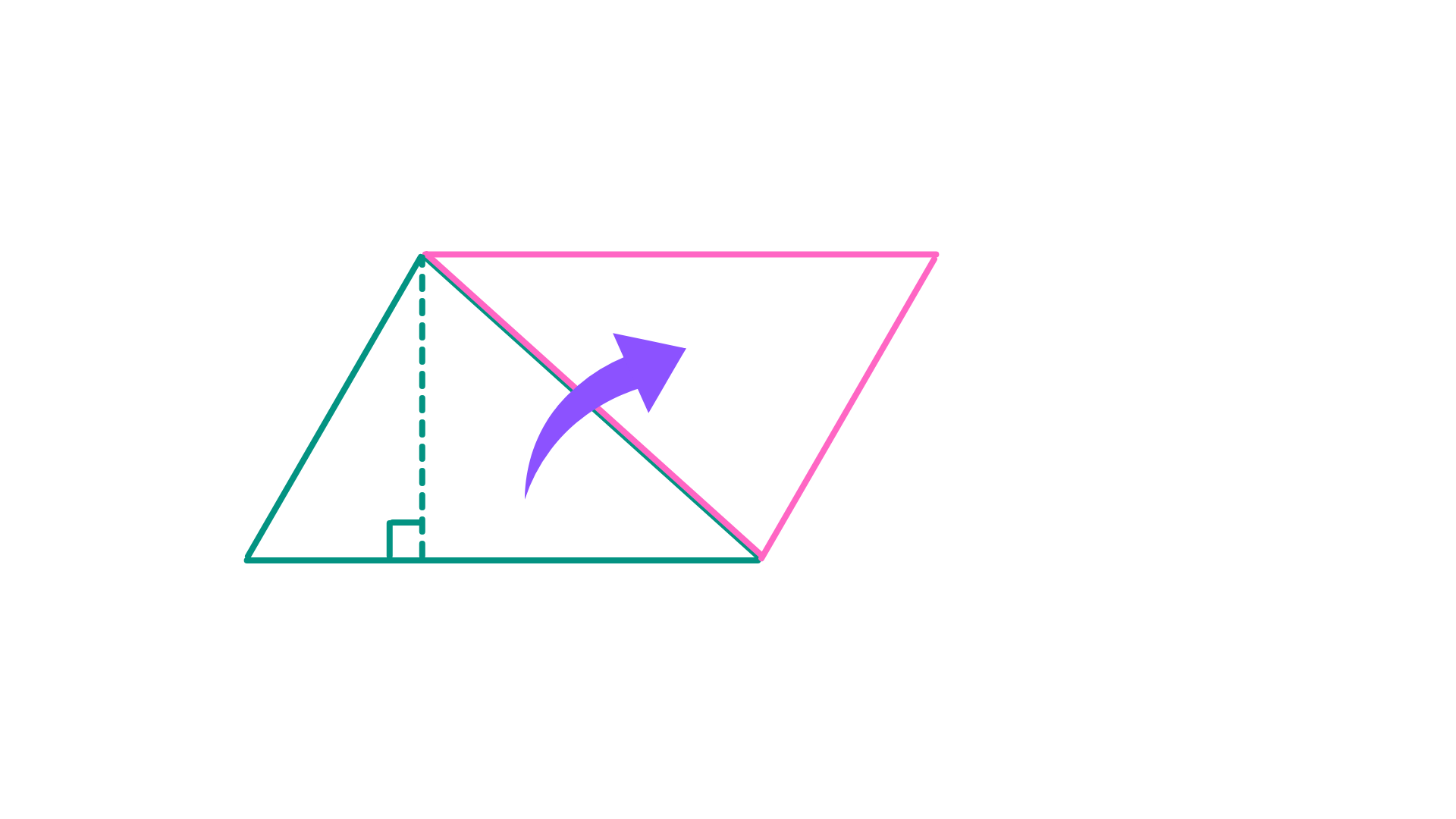57.png 同じ三角形を回転させてくっつけることで、平行四辺形が作れます。
平行四辺形の面積は底辺×高さで求まるので、その半分が三角形の面積だとわかります。
三角形の面積＝平行四辺形の面積÷2
　　　　　　＝底辺×高さ÷2

また、よく混乱しますが、高さが三角形の内部にないこのような場合ではどう求めればいいでしょうか。
54.png
この場合の高さはここの部分になります。
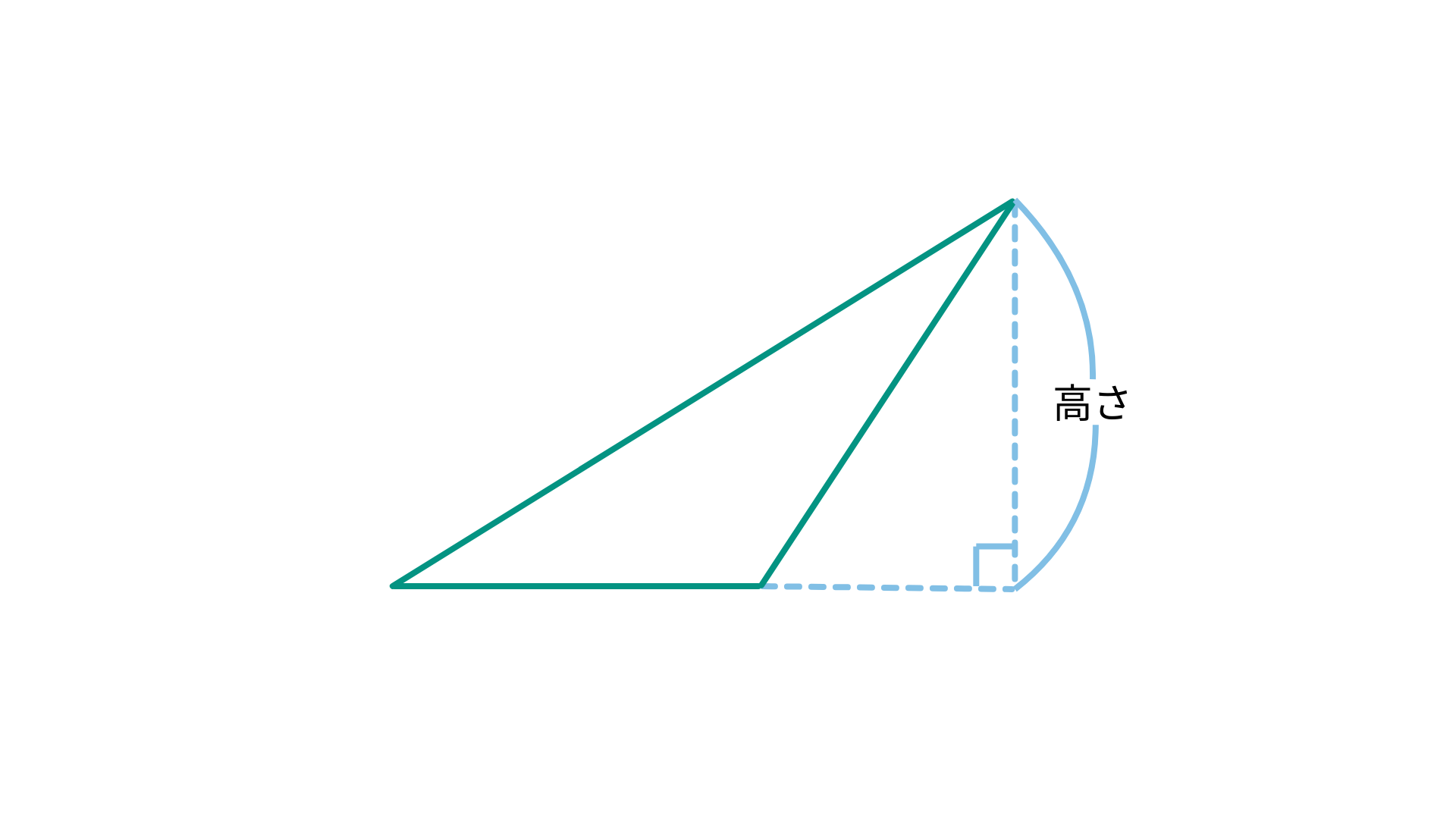
56.png
これも同様に同じ三角形を使って平行四辺形を作るとわかります。
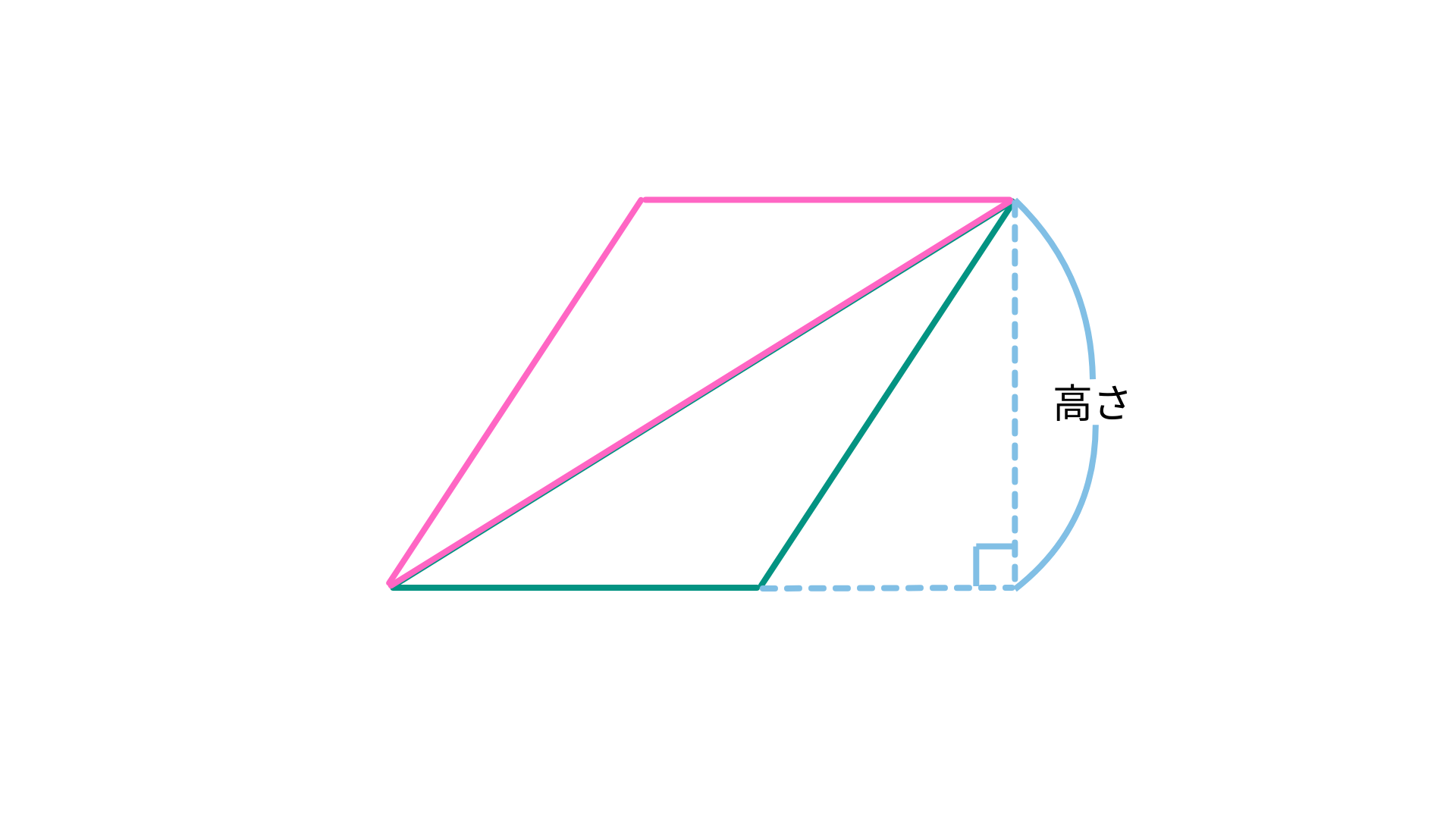
55.png
高さがどこなのかわからなくなる場合は平行四辺形をイメージしてどこが高さなのかを確かめるようにしましょう。

【中学生向け】3辺がわかっている場合（三平方の定理）

三平方の定理がわかっていると高さがわからなくても、3辺の長さから三角形の面積を求めることができます。
三平方の定理を理解していない方はこちらの記事を先に読むことをおすすめします。
三平方の定理（ピタゴラスの定理）とは？計算の仕方と証明をやさしく解説！

例えば3辺の長さが15, 14, 13のとき三角形の面積を求めてみましょう。
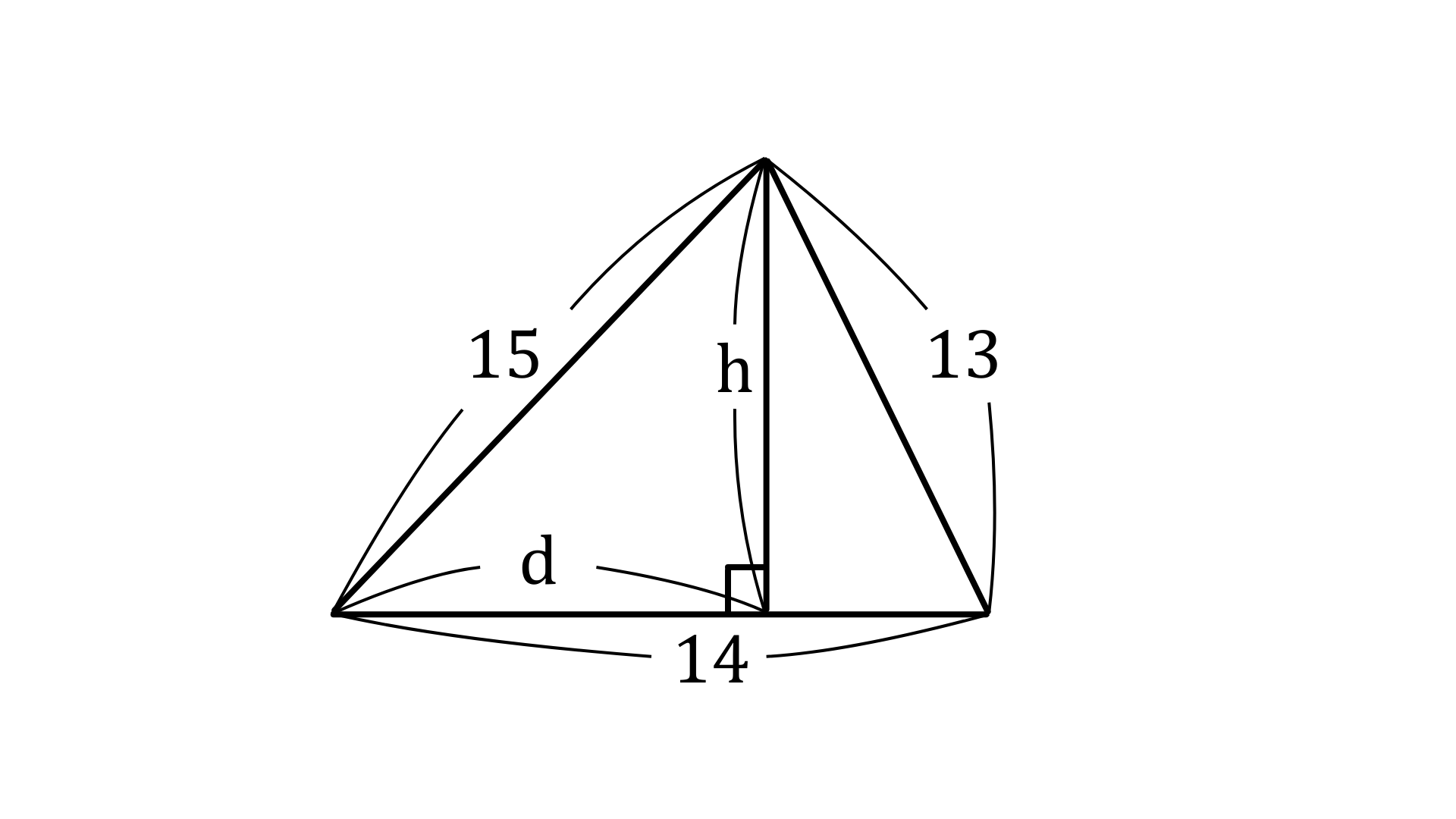
三角形の面積9.png
垂線で分かれた2つの三角形それぞれで三平方の定理を使うと
$15^2=h^2+d^2$… ①
$13^2=h^2+(14-d)^2$ … ②
①-②より、
$56=28d-196$
$28d=252$
$d=9$
①に代入すると、
$h^2=225-81$
$h^2=144$
$h=12$
と求まります。
よって三角形の面積は
$14×12÷2=84$（答）

次にこれを一般化した形を紹介します。
それぞれの辺をa,b,cとすると
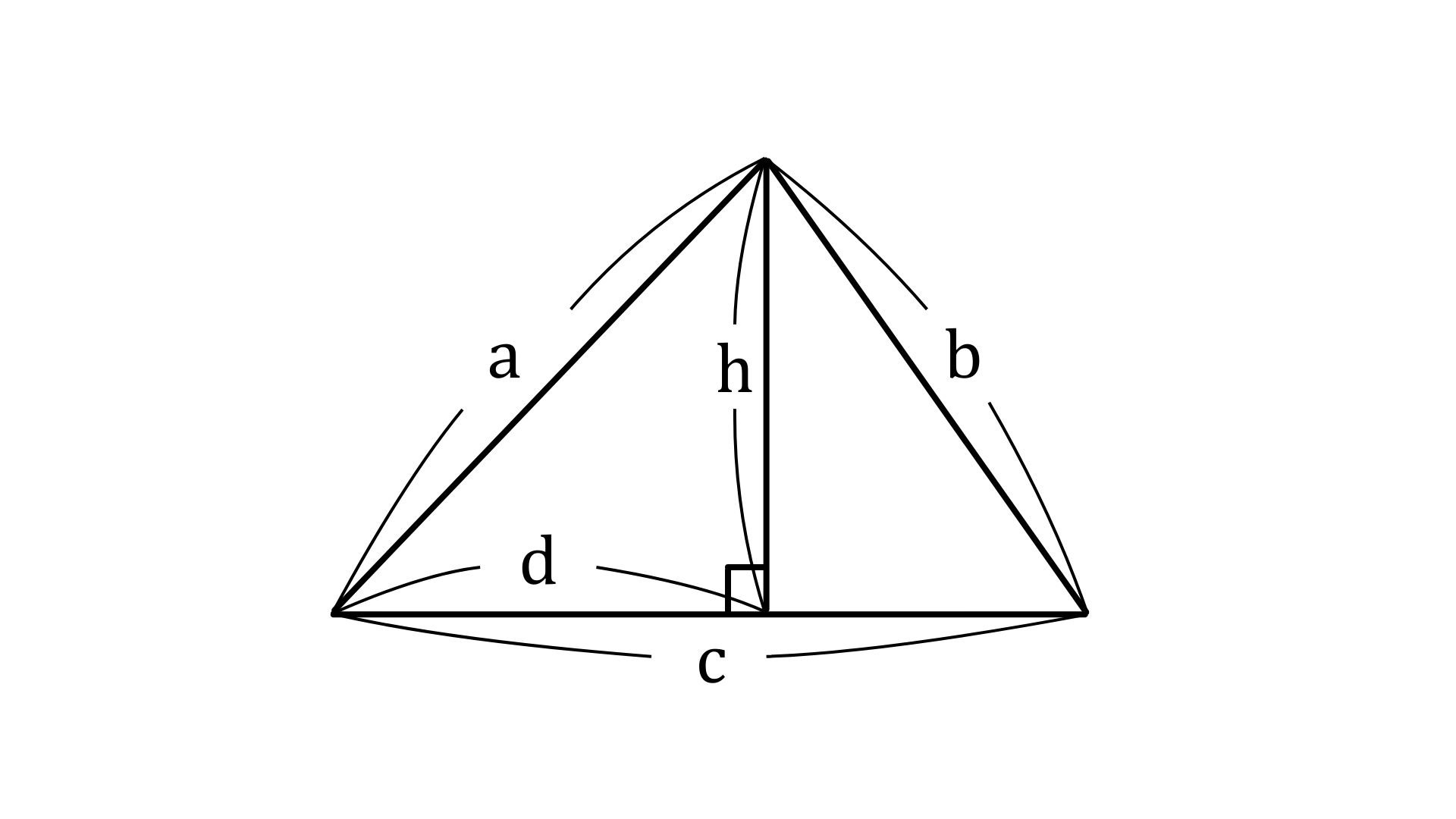
三角形の面積10.jpg
$a^2=h^2+d^2$… ①
$b^2=h^2+(c-d)^2$… ②
①-②より
$a^2-b^2=2cd-c^2$
$d=\frac{a^2-b^2+c^2}{2c}$

これを①に代入すると
$h=\sqrt{a^2-(\frac{a^2-b^2+c^2}{2c})^2}$
$h=\frac{1}{2c}\sqrt{4a^2c^2-(a^2-b^2+c^2)^2}$
よって三角形の面積は
$\frac{1}{2}ch=\frac{1}{4}\sqrt{4a^2c^2-(a^2-b^2+c^2)^2}$… ③
となります。

複雑な式ですが、正三角形のときはa=b=cなのでかなりすっきりした式になります。
$\frac{1}{2}ch=\frac{1}{4}\sqrt{4a^4-a^2}=\frac{\sqrt{3}}{4}a^2$
この形だけでも覚えておくことをおすすめします。

【高校生向け】3辺がわかっている場合（ヘロンの公式）

上記の③の式は暗記するのも大変ですが、計算するのも大変です。そこで式変形して覚えやすく、計算しやすくしたヘロンの公式を紹介します。

③のルートの中を$a^2-b^2=(a+b)(a-b)$の形で因数分解すると
$\frac{1}{4}\sqrt{(2ac+a^2-b^2+c^2)(2ac-a^2+b^2-c^2)}$

$=\frac{1}{4}\sqrt{((a+c)^2-b^2)(b^2-(a-c)^2)}$

$=\frac{1}{4}\sqrt{(a+b+c)(a-b+c)(a+b-c)(-a+b+c)}$

$=\sqrt{\frac{(a+b+c)(a-b+c)(a+b-c)(-a+b+c)}{16}}$

$=\sqrt{\frac{(a+b+c)}{2}\frac{(a-b+c)}{2}\frac{(a+b-c)}{2}\frac{(-a+b+c)}{2}}$


ここで$s=\frac{a+b+c}{2}$とおくと
$=\sqrt{s(s-a)(s-b)(s-c)}$

と整理ができます。

三角形の面積11.png

このヘロンの公式のほうが形として覚えやすく、また計算も早くなるため覚えておくとよいでしょう。

【高校生向け】3辺の長さと内接円の半径がわかっている場合

三角形の3辺がわかっていてさらに内接円の半径がわかっている場合の公式もあります。
内容としては難しくないので小中学生の方も理解できる内容だと思います。
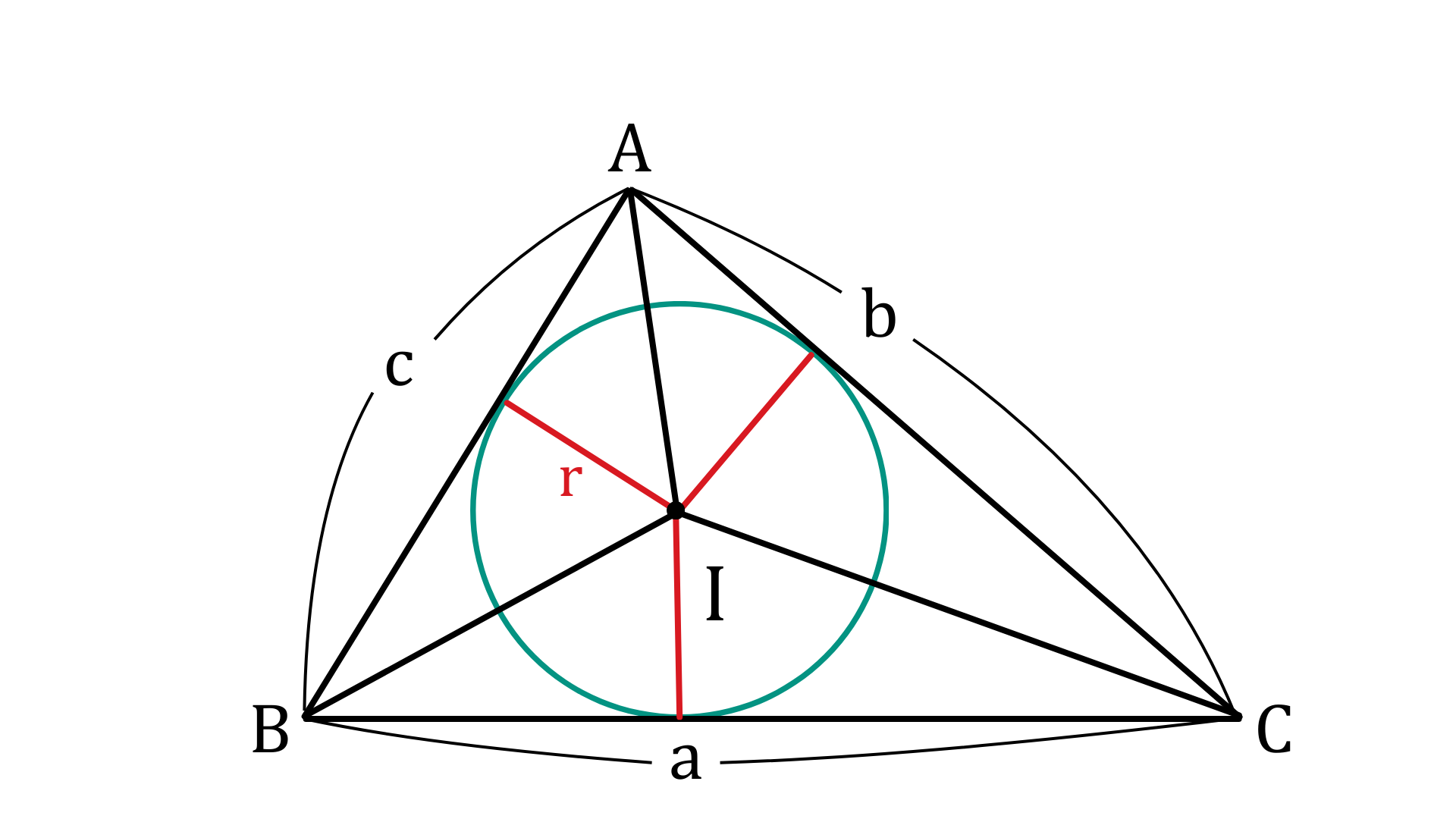
三角形の面積12.png
内接円の中心をIとすると三角形の面積は
△ABC=△BCI+△ACI+△ABI
のため
△ABC＝$\frac{1}{2}ar+\frac{1}{2}br+\frac{1}{2}cr$
$=\frac{1}{2}r(a+b+c)$
となります。
三角形の面積13.png

【高校生向け】2辺とその間の角がわかっている場合

2辺とその間の角がわかっている場合、三角比を使って三角形の面積を求めることができます。
三角比を理解していない方はこちらの記事を先に読むことをおすすめします。
三角比(sin, cos, tan)入門！表の使い方とわかりやすい公式の覚え方を紹介！

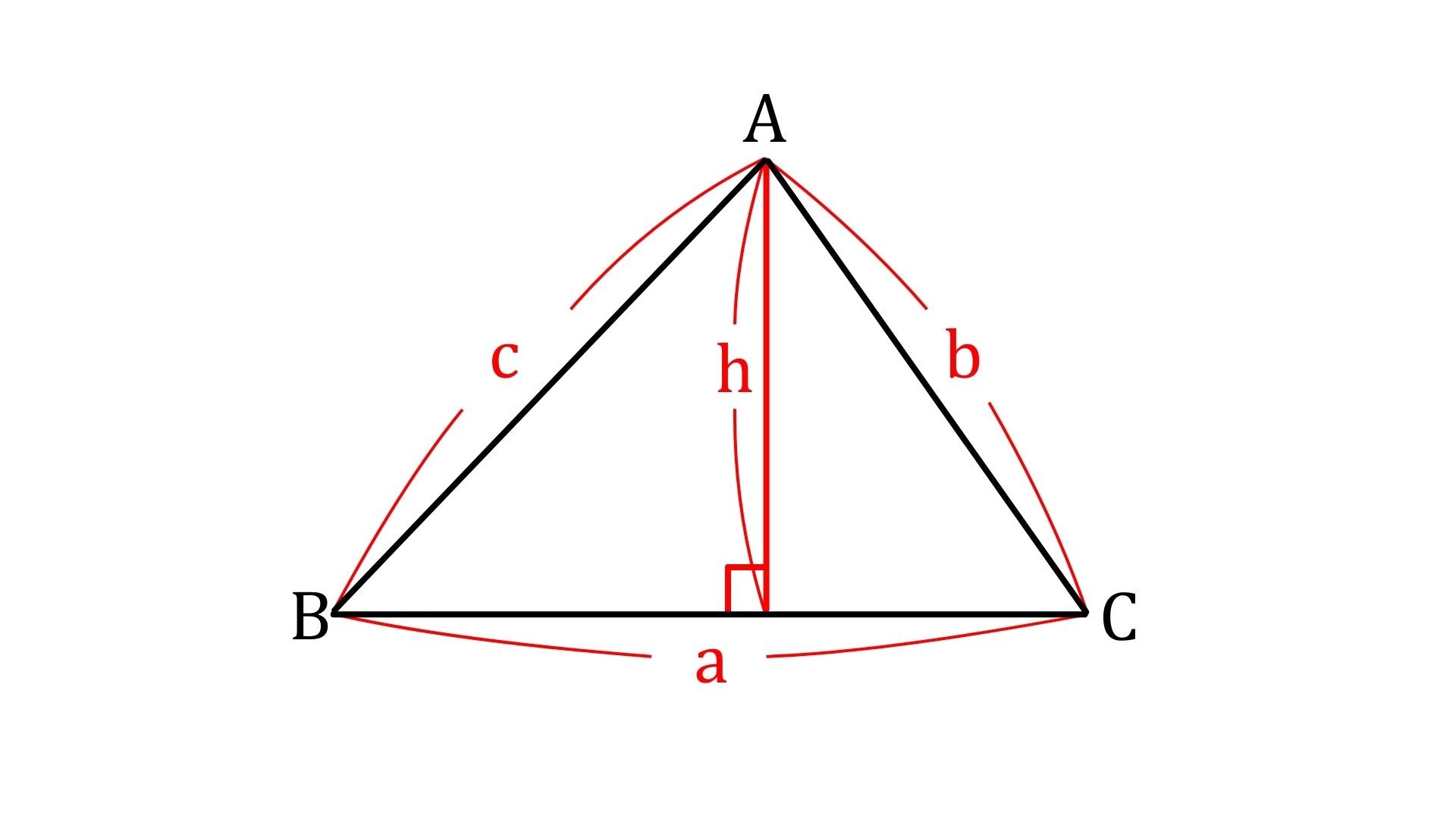
三角形の面積14.jpg

△ABC=$\frac{1}{2}ah$
$\sin{B}=\frac{h}{c}$なので、$h=c\sin{B}$を代入すると
△ABC=$\frac{1}{2}ac\sin{B}$
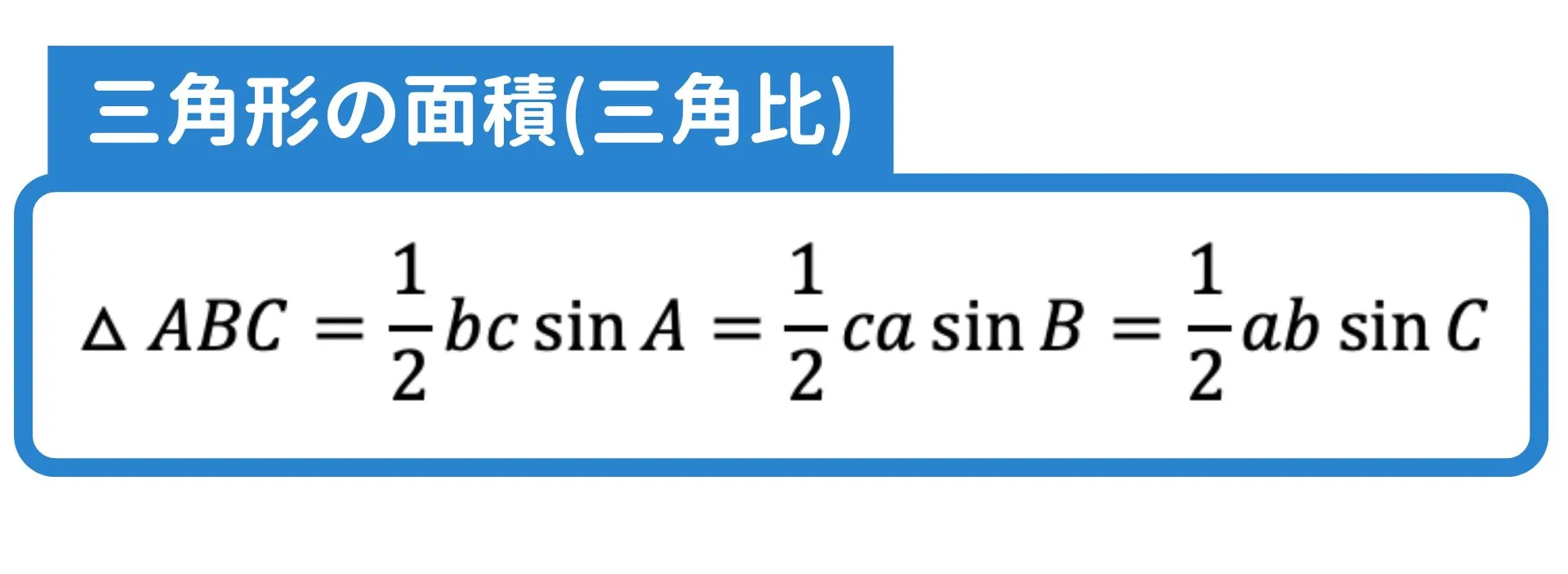
△ABC$=\frac{1}{2}bc\sin{A}=\frac{1}{2}ca\sin{B}=\frac{1}{2}ab\sin{C}$
と言えます。

三角形の面積15.png

【高校生向け】平面座標上の三角形の面積の求め方

平面座標上の三角形の点がわかっている場合の面積の求め方を紹介します。
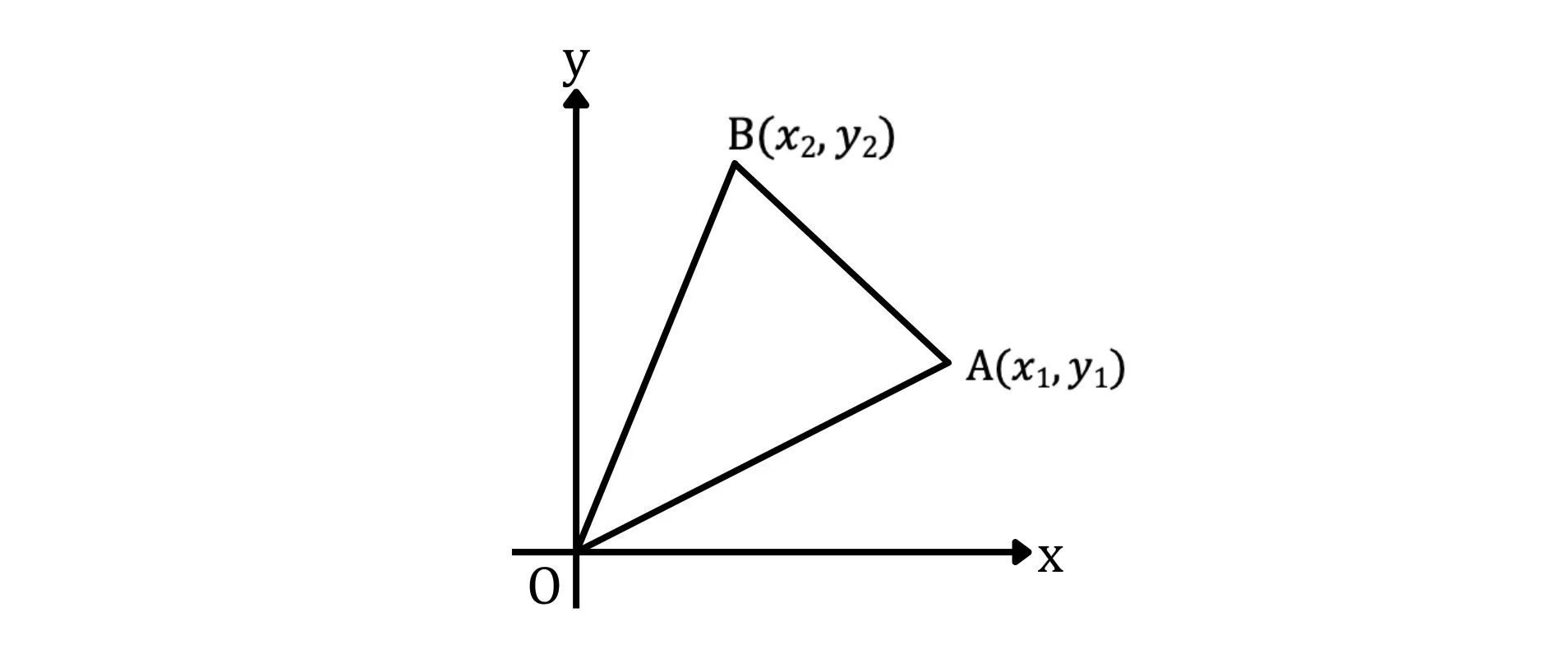
三角形の面積16.png
点と直線の距離を使って△OABの面積を求めていきます。
点BとOAの距離は点と直線の距離の公式より
$\frac{|y_1x_2-x_1y_2|}{\sqrt{y_1^2+(-x_1)^2}}$
また、OA=$\sqrt{x_1^2+y_1^2}$なので
△OAB=$\frac{1}{2}\sqrt{x_1^2+y_1^2}\frac{|y_1x_2-x_1y_2|}{\sqrt{y_1^2+x_1^2}}$
=$\frac{1}{2}|y_1x_2-x_1y_2|$
=$\frac{1}{2}|x_1y_2-y_1x_2|$
と表すことができます。
三角形の面積19.png
これは原点を含む場合の公式のため、原点を含まない三角形の場合は平行移動してから公式に当てはめるように注意してください。

【高校生向け】ベクトルを用いた三角形の面積の求め方

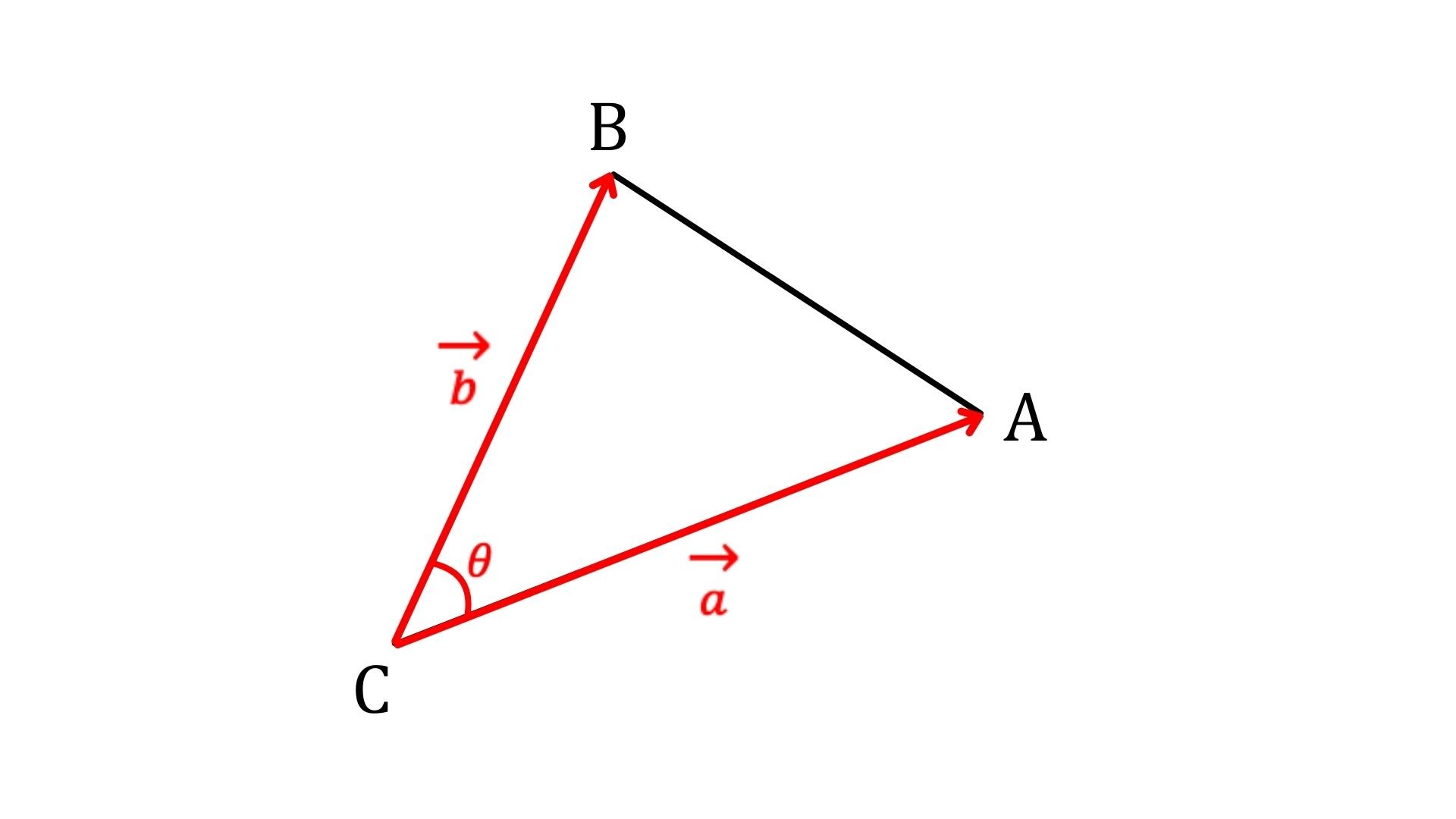
三角形の面積18.jpg

三角比を用いた面積の公式より
△ABC=$\frac{1}{2}ab\sin{C}$
$=\frac{1}{2}|\vec{a}||\vec{b}|\sin{\theta}$… ①
三角形の角度なので0°<$\theta$<180°、よってsinは正の値を取るので
$\sin{\theta}=\sqrt{1-\cos^2{\theta}}$… ②

ベクトルの内積の定義から
$\vec{a}・\vec{b}=|\vec{a}||\vec{b}|\cos \theta$
なので
$\cos \theta~=\frac{\vec{a}・\vec{b}}{|\vec{a}||\vec{b}|}$ … ③

①②③より整理すると
△ABC
$=\frac{1}{2}|\vec{a}||\vec{b}|\sqrt{1-(\frac{\vec{a}・\vec{b}}{|\vec{a}||\vec{b}|})^2}$
$=\frac{1}{2}|\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}・\vec{b})^2}$

こちらはベクトルの成分が分かれば非常に簡単に計算できる公式で平面座標だけでなく、空間座標にも使え、非常に便利なため覚えておくとよいでしょう。
三角形の面積17.png

練習問題

問.底辺が4高さが2の三角形の面積を求めなさい


解答はこちら

問.1辺が4の正三角形の面積を求めなさい


解答はこちら

問.3辺が13,21,20の三角形の面積を求めなさい


解答はこちら

問.3辺が6,6,4の二等辺三角形の内接円の半径が$\sqrt{2}$のとき三角形の面積を求めなさい


解答はこちら

問.2辺が4, 6その間の角度が30°の三角形の面積を求めなさい


解答はこちら

問.原点とA(-1,ー2,1)β(2,2,0)を頂点に持つ三角形の面積を求めなさい


解答はこちら

まとめ

いかがでしたでしょうか。本記事では、三角形の面積の求め方について小学生で学ぶ基本的な方法から、高校生で学ぶ発展的な方法を解説しました。

小学生の皆さんは、三角形の「高さ」がどこなのか、について注目するようにしましょう。

中学生の皆さんは、三平方の定理をうまく活用してみましょう。

高校生の皆さんは、これまでの方法以外にもたくさん三角形の面積の求め方を習います。場面に合わせた解き方を選べるよう練習を積みましょう。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

この記事を家族や友人に教える

明光プラスで読みたい記事のテーマを募集

明光プラスでは読者の方のご期待に沿えるように読みたい記事のテーマを募集しています。ぜひ下のリンクからアンケートにお答えください。

読みたい記事のテーマをリクエストする

関連タグ

#中学生 #小学生 #数学 #算数 #高校生

あわせて読みたい記事

タグ一覧

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

Home > 明光プラス > 学習 > 三角形の面積の求め方！学齢に応じた公式の一覧となぜそうなるのかを解説します