2025.05.01
部分分数分解は簡単！やり方と公式を3つのパターンと4つのステップでやさしく解説します！
部分分数分解という言葉自体がややこしく苦手意識を持っている方も多いのではないでしょうか。
数Ⅲの積分で部分分数分解が必要になることもあり、大学入試で出ることもあるためしっかりと理解しておきたいところです。
部分分数分解は要領をおさえてしまえばとても簡単です。ぜひこの機会にしっかりと理解して苦手意識をなくしていきましょう。
部分分数分解とは？何のためにやるのか
部分分数分解とは分数の式を単純な分数に分けるテクニックのことです。
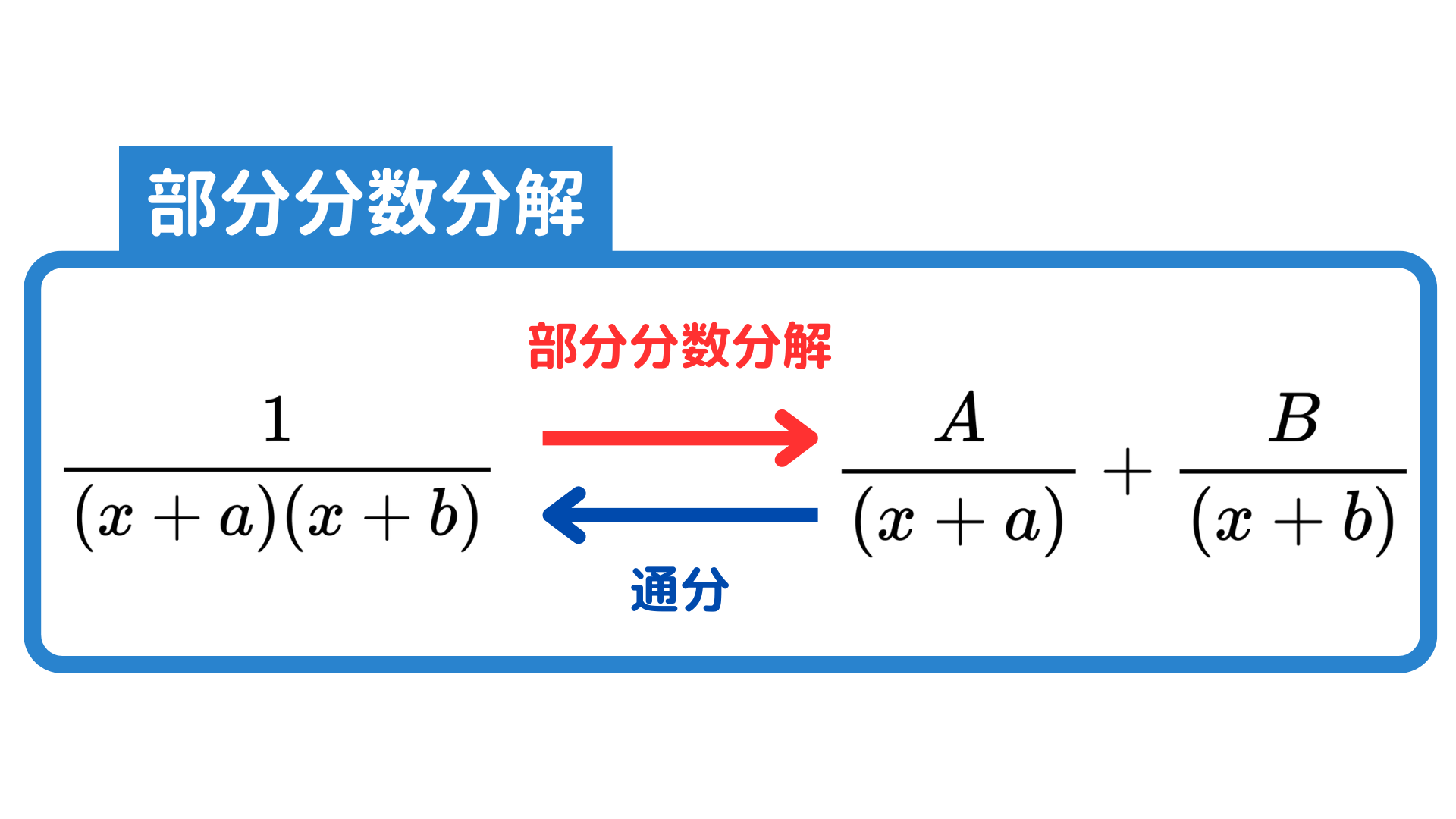
部分分数分解をすることで、分母が掛け算で表されるような複雑な式を、分母が単純な形の足し算に直すことができます。左向きに式を整えることを通分と言うので、部分分数分解は通分の逆の操作です。
このように分解することで、積分しやすい形になるなどメリットがあるのが部分分数分解です。
部分分数分解の覚えるべき3つの公式パターン
部分分数分解には、大きく分けて3つの公式のパターンがあります。
これら2つの公式は基本のパターンで共通テストでも頻出です。$A,B$は定数なので次のように通分することで計算することができます。
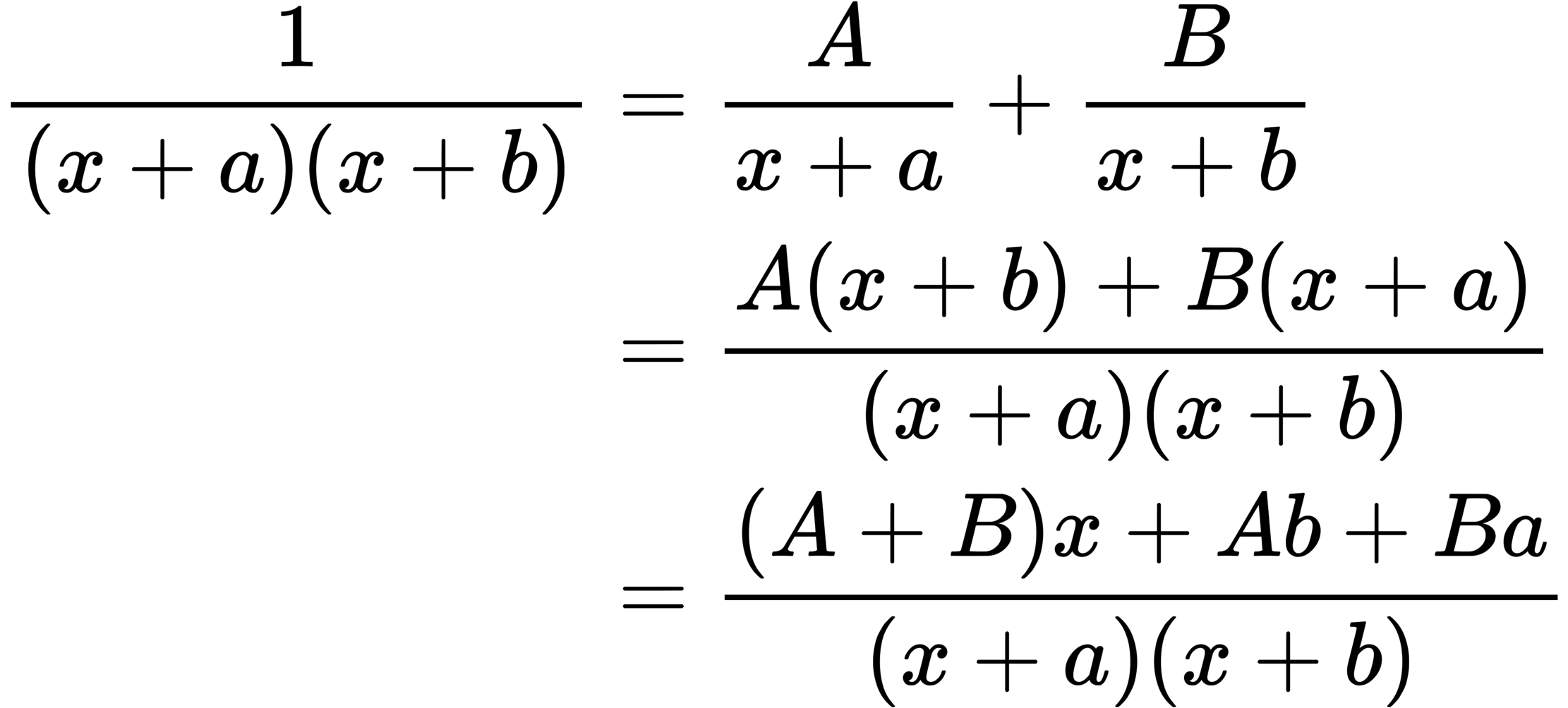
$x\neq -a, -b$ のとき両辺は等しいので元々の式の$x$の係数が0であること、定数項が1であることから次の連立方程式を解くことで$A,~B$の計算が可能です。
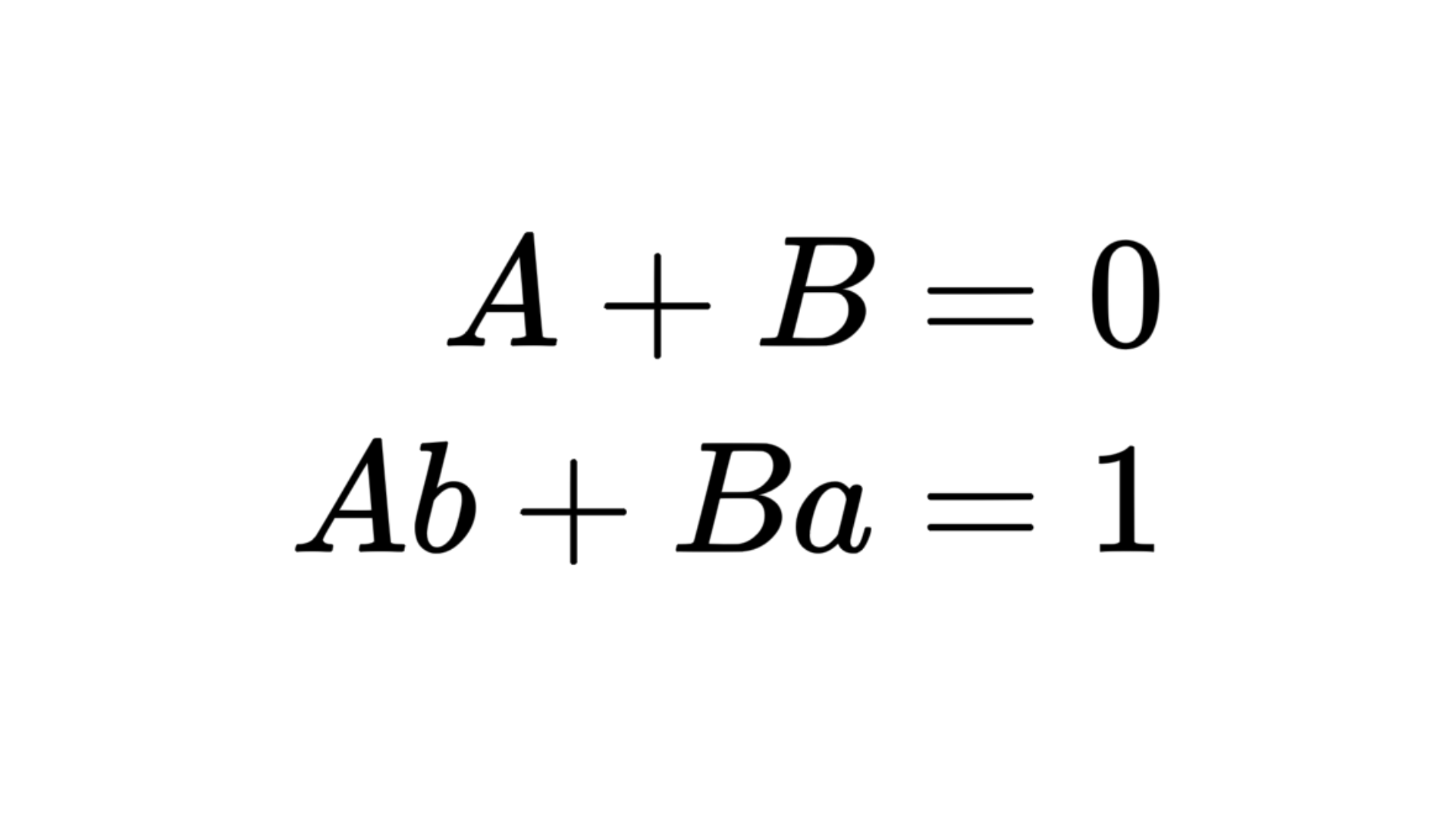
(2)の公式も同様に計算することで$A,B$を導くことができます。
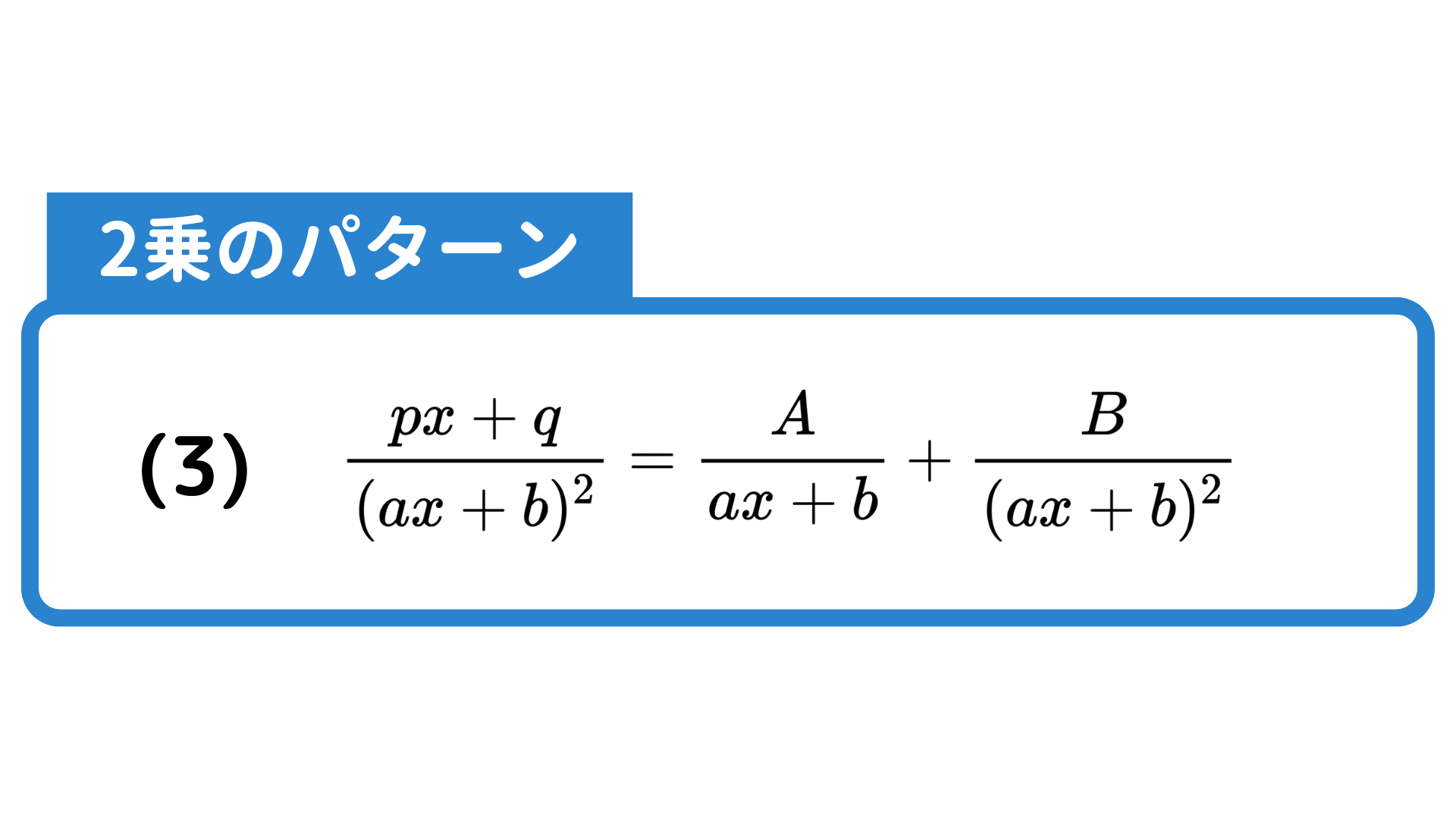
2乗の場合、同じ式が分母に並んでしまうため、(2)のようにしても左辺の式を導くことができません。そのためこの(3)の公式のように1乗の分母と2乗の分母を並べると覚えておきましょう。
部分分数分解のやり方4ステップ！
部分分数分解をするときは次の4つの手順を覚えておき実行しましょう。
ステップ１. 分母を因数分解する
まずは式の分母を因数分解します。すでに因数分解されているときはこのステップは飛ばします。
例：
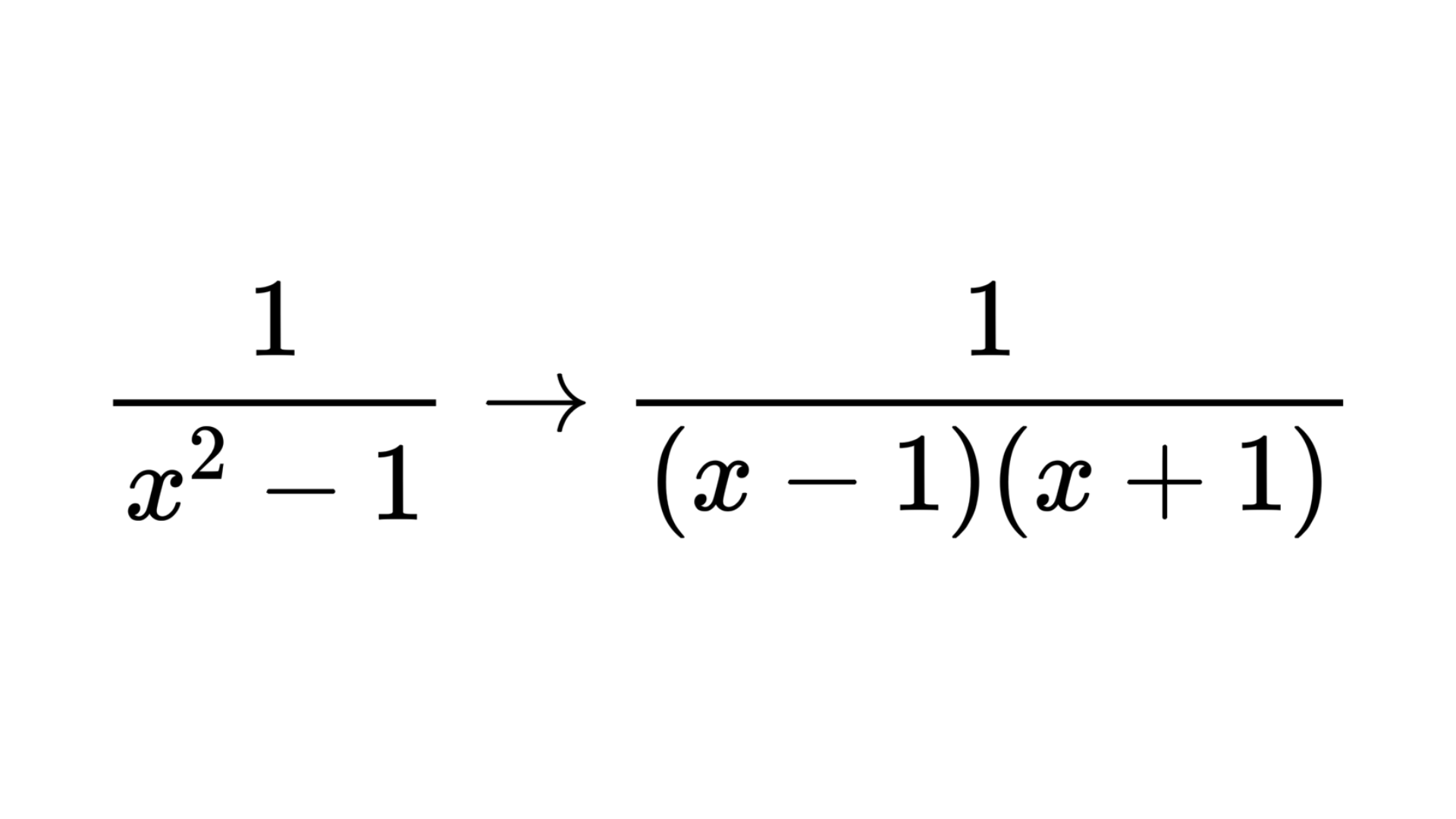
ステップ２.公式のパターンに当てはめて式を立てる
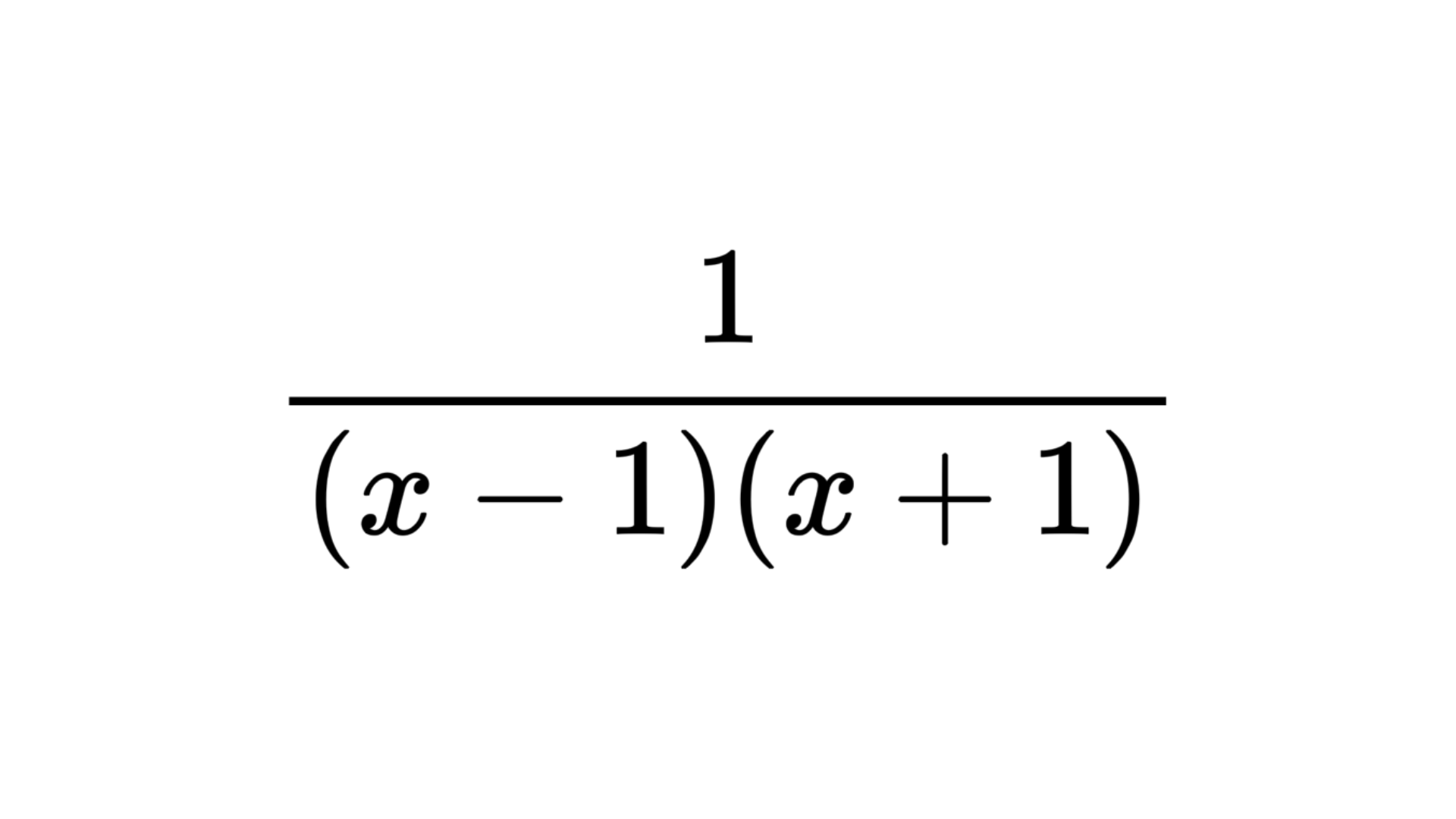
は公式(1)のパターンなので、次のように式を立てます。
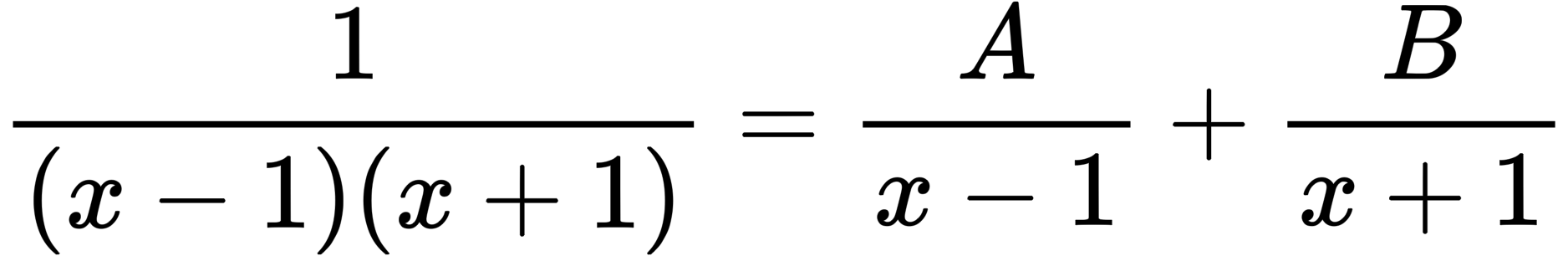
ステップ３.両辺に共通の分母をかけて分数を消す
先ほどは通分しましたが、やっていることは一緒です。途中式で書く量が少なくなるため、こちらのほうがおすすめです。
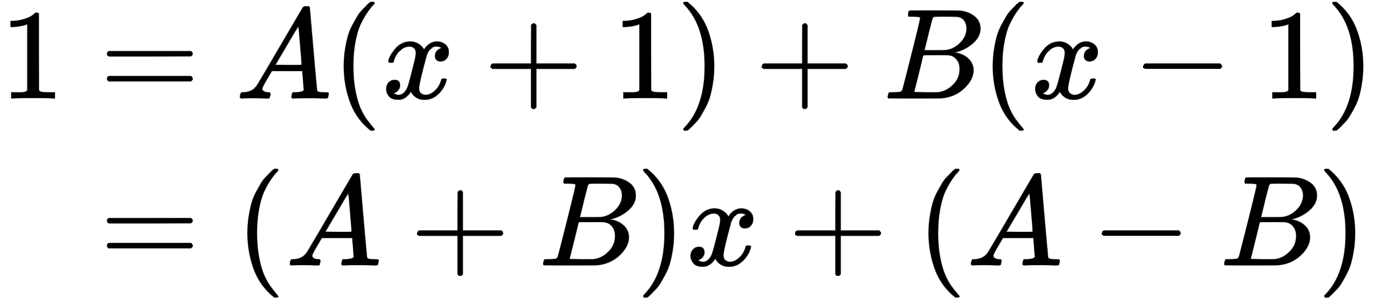
ステップ４.連立方程式を解く
$x$の1次の係数と定数項を比較すると
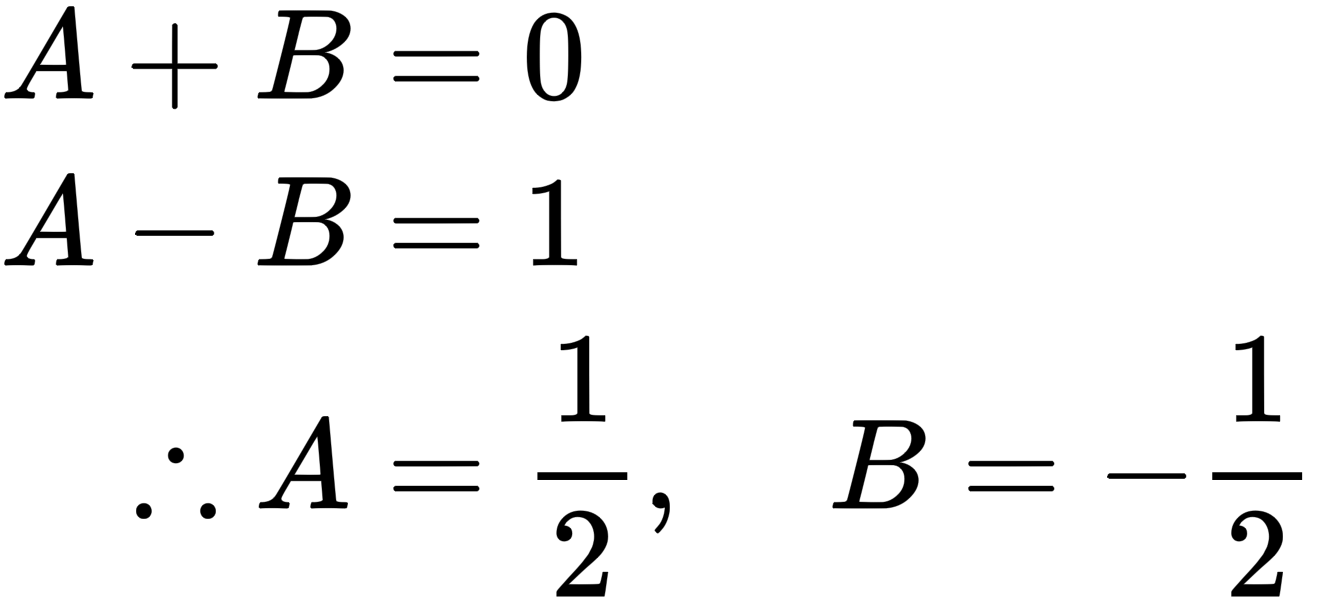
連立方程式の解き方はこちらの記事で詳しく解説しています。もし難しい連立方程式で悩んでしまう場合にはこちらの記事を参考にしてください。
連立方程式は簡単！基本問題の解き方から文章題の解き方まで徹底解説します
練習問題
問.$\frac{1}{(2x-1)(x+2)}$を部分分数分解しなさい
問.$\frac{2x+3}{(x+1)(x+2)}$を部分分数分解しなさい
問.$\frac{3x+5}{(x+1)^2}$を部分分数分解しなさい
まとめ
いかがでしたでしょうか。本記事では、部分分数分解について、3つの公式のパターンや4ステップのやり方を解説しました。
部分分数分解は大学受験では頻出の計算方法ですので、やり方を覚えて、さまざまな式で応用できるように理解しておきましょう。
教室数・生徒数No.1の個別指導塾！
明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。
お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。
この記事を家族や友人に教える
明光プラスで読みたい記事のテーマを募集
明光プラスでは読者の方のご期待に沿えるように読みたい記事のテーマを募集しています。ぜひ下のリンクからアンケートにお答えください。
あわせて読みたい記事
-
微分とは？微分は○○です！定義・公式・使い方を解説
2025.07.07
高校数学の教育課程で避けては通れない微分。苦手に感じていたり、つまずいたりしてしまう方も多いのではないでしょうか。 本記事では、微分とは何かという定義から、基本公式・実際の使い方・例題・応用までを、...
-
三角関数（sin, cos, tan）入門！公式をわかりやすく覚える方法を紹介！
2025.06.26
三角関数では$\sin$(サイン),$\cos$(コサイン),$\tan$(タンジェント)や$\theta$(シータ)といった聞きなれない呪文のような言葉が多く出てくるのに加え、覚える公式が多いため...
-
三角比(sin, cos, tan)とは？覚え方と三角比の表も紹介！
2025.06.20
三角比ではsin(サイン),cos(コサイン),tan(タンジェント)やθ(シータ)といった聞きなれない呪文のような言葉がでてくるうえに、覚えることも多いため苦手意識を持っている方も多いのではないで...
タグ一覧
おすすめ記事
-
【無料テンプレート付き】勉強計画の立て方｜効率的な学習を実現する勉強計画表とは？
2025.07.03
「勉強しなきゃ」と思っても、いざ机に向かうと何から始めればいいかわからない…そんな経験はありませんか？ 実は、成績アップに欠かせないのが“計画的な学習”です。 目標に向かって着実に前進するに...
-
【小論文の書き方】構成・テクニックを例文付きで解説！高校生向け完全ガイド
2025.06.26
「受験科目に小論文があるけれど、どうやって書けばよいかわからない」 というように、小論文に苦手意識をもつ高校生は多いのではないでしょうか。 小論文には書き方や構成の仕方...
-
歴史の勉強法のコツを紹介！楽しく覚える方法も解説します！
2024.04.30
歴史の勉強について、どんな印象を持っていますか？ 「覚えることが多い」「つまらない」「勉強する意味がわからない」。 歴史の勉強に苦手意識を持っている人は、このように捉えていることが多いです。...
-
テスト勉強してない！不安な中でも前日・当日にできることとは？
2022.06.15
翌日に迫ったテスト。「勉強してない！」と焦り出したとき、一体どのように対策すればよいのでしょうか。 勉強は日ごろの積み重ねによって力がついてくるものです。テスト勉強もスケジュールを立てて計画...
