明光義塾へ
学習

2025.07.04

三平方の定理（ピタゴラスの定理）とは？計算の仕方と証明をやさしく解説！

三平方の定理サムネイル

もくじ

三平方の定理(ピタゴラスの定理)とは？


三平方の定理（ピタゴラスの定理）は、直角三角形において斜辺の長さをc、ほかの2辺をa,bとした時に、以下の式が成り立つという定理です。


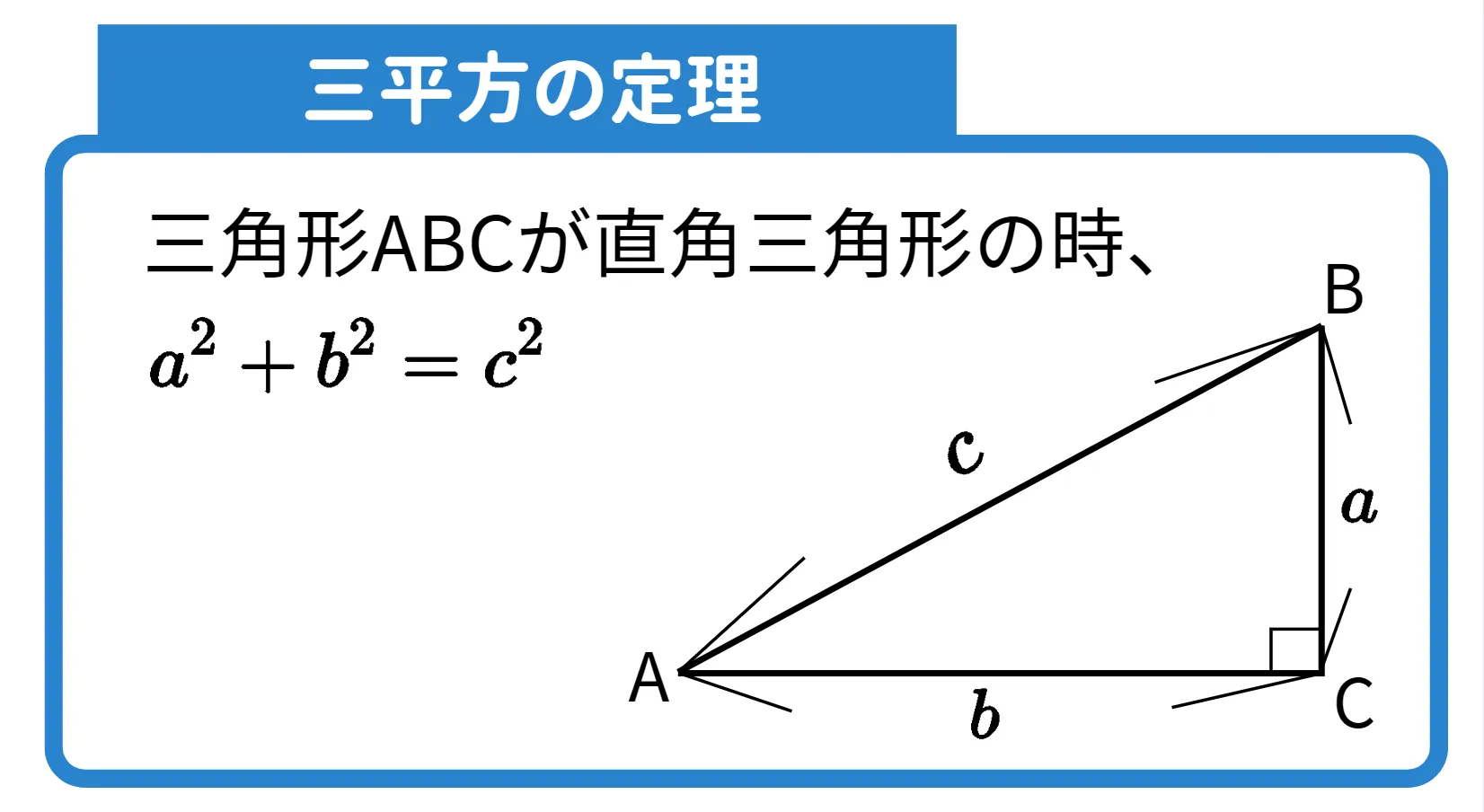
三平方の定理公式

3辺の長さa,b,cのうち2つがわかれば、残りの1辺の長さを求めることができます。


また、三平方の定理は逆も成り立ちます。三角形の3辺の長さの関係が


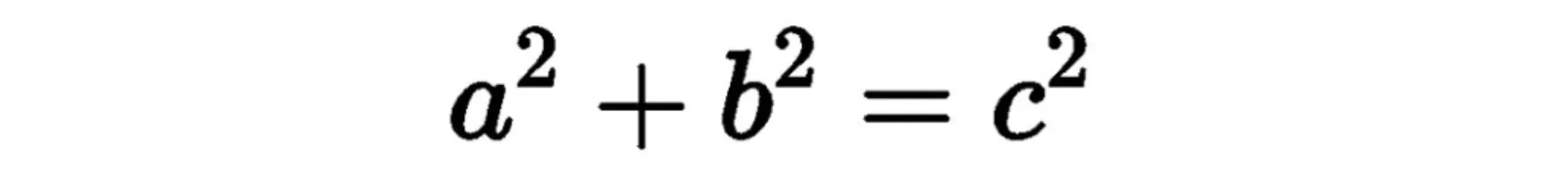
三平方の定理の逆

となる場合、その三角形はすべて直角三角形であるといえます。


この時cが一番大きい値であり、直角三角形で一番長い斜辺であることを理解しておきましょう。

この定理を用いることで、xy平面上における2点間の距離を求めることができます。

三平方の定理(ピタゴラスの定理)の応用

xy平面上における2点間の距離


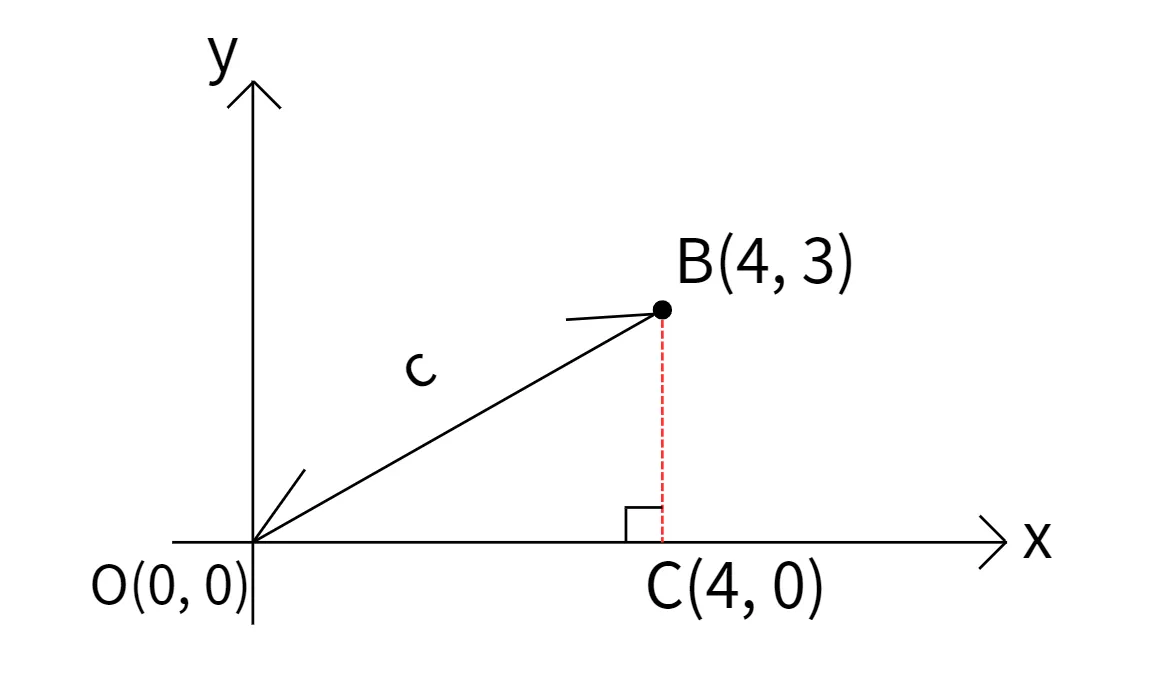
2点間の距離と三平方の定理

原点O(0,0)からB(4,3)までの距離cは、点Bからx軸に垂線をおろしてできる直角三角形OBCに着目することで、以下のように計算できます。


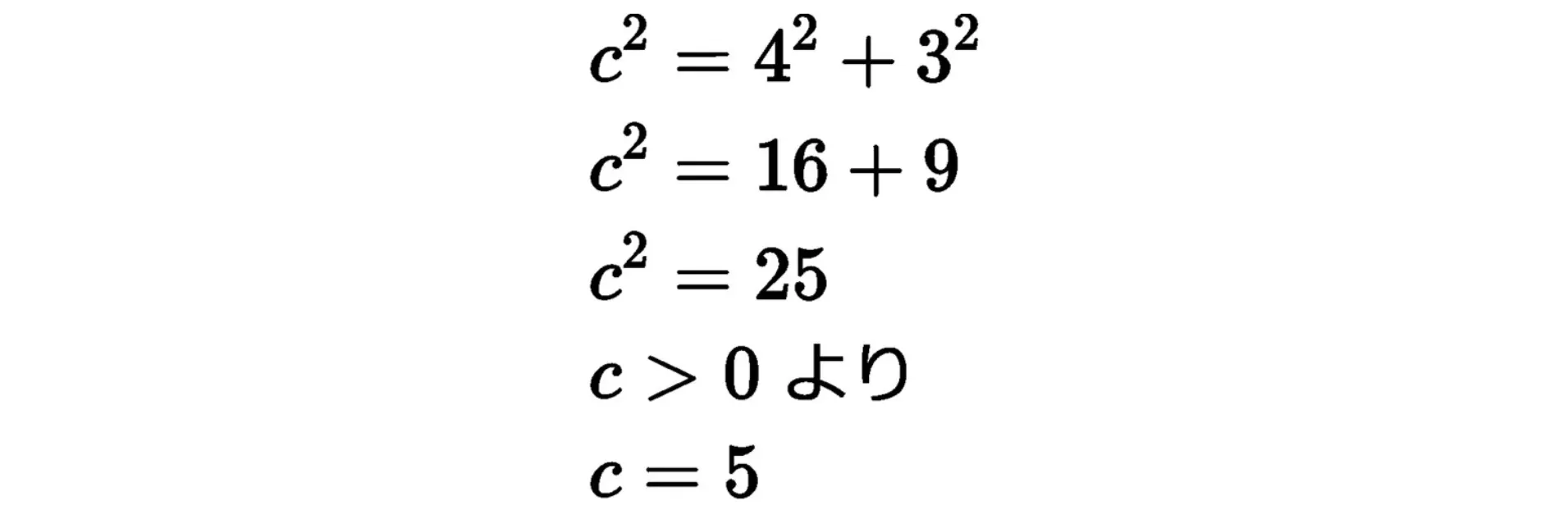
2点間の距離

もちろん原点からでなく、座標がわかっていればxy平面のどこに2点があっても計算ができます。

紐を用いた直角の作図

三平方の定理を活用し、紐を使って直角を作ってみましょう。

例えば12mの紐を使い、3m、4m、5mに分割して三角形を作ると上記と同じ辺の比が3:4:5の直角三角形が出来上がります。


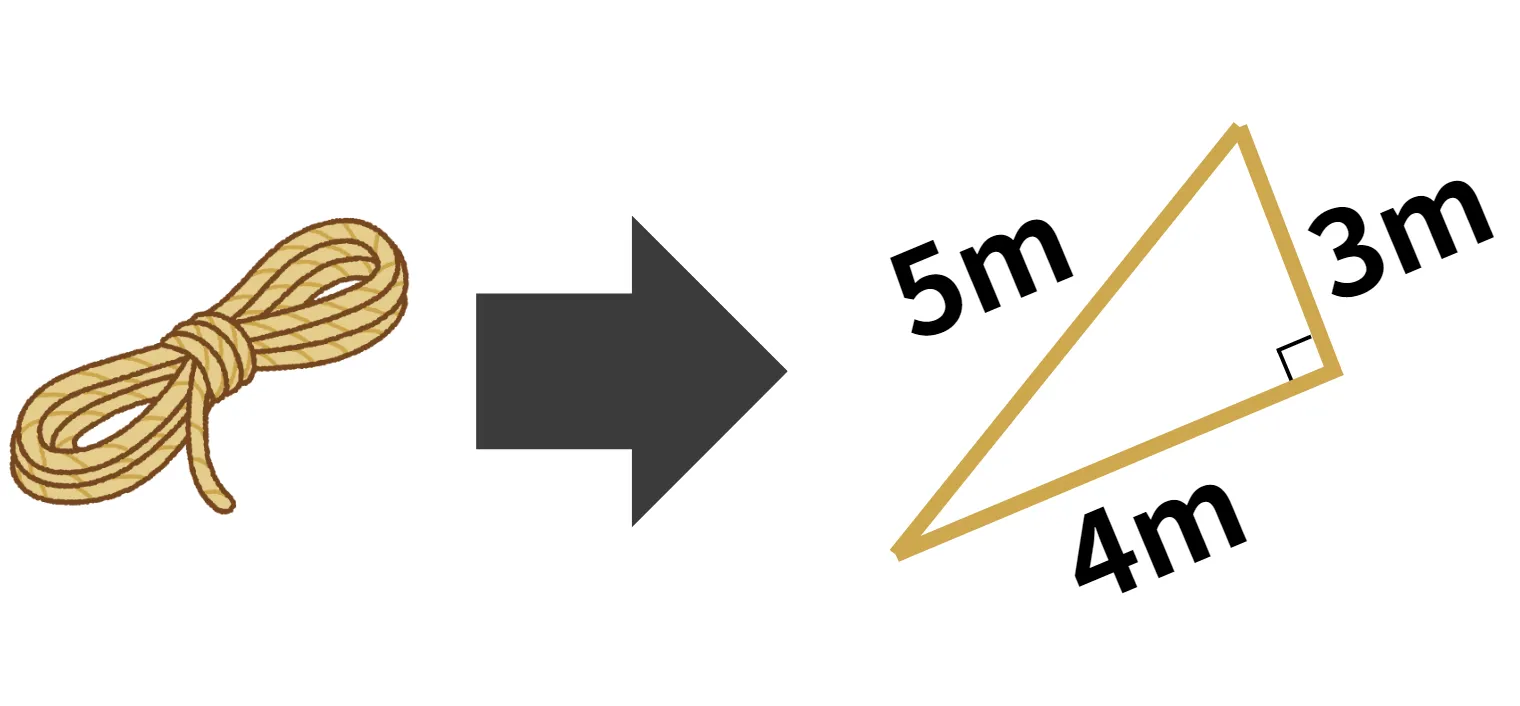
紐を用いた直角の作図

直角を示すものがない場合でも、三平方の定理を満たす3辺の長さを用いることで、直角を簡単に作図することができます。

特別な直角三角形の3辺の比

三平方の定理の問題でよく出てくる三角形は、「特別な直角三角形」と呼ばれています。ここでは代表的な3つの直角三角形について紹介します。


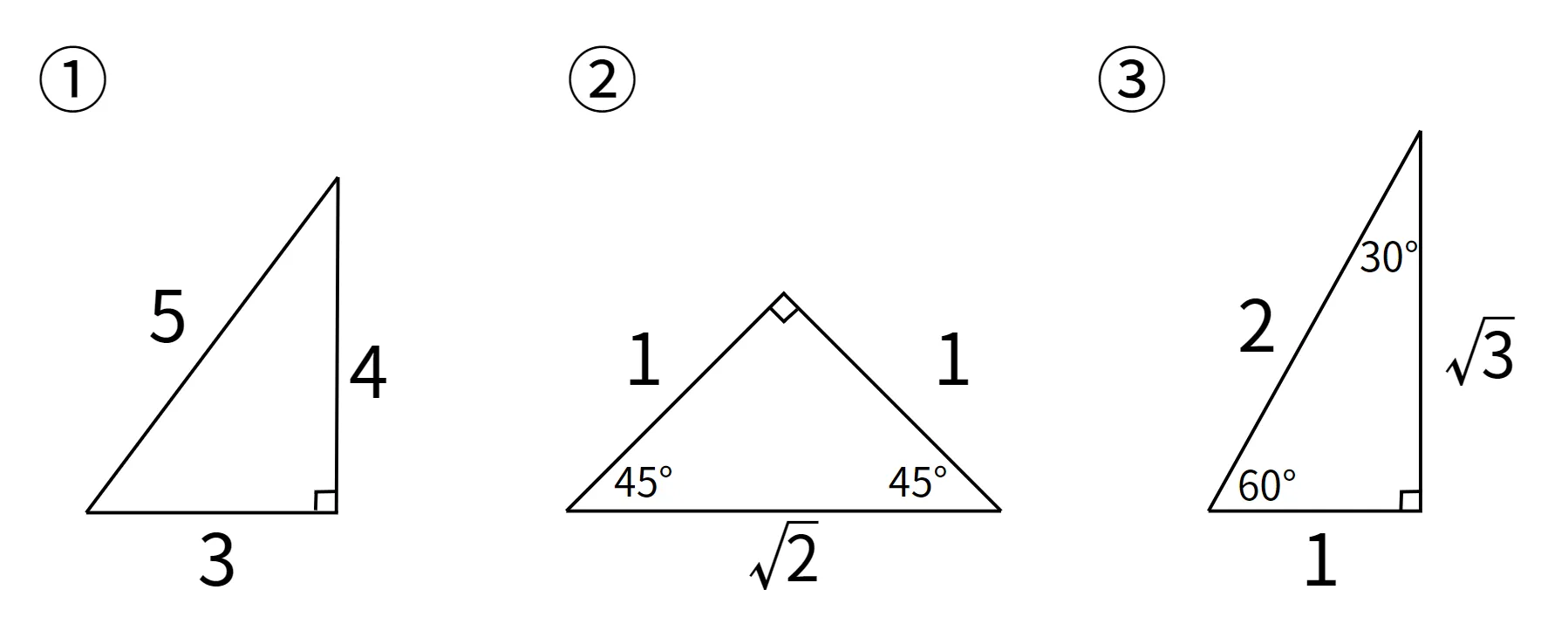
代表的な直角三角形

①は、辺の比がすべて自然数になる直角三角形の中で、一番簡単なものです。

長さがすべて自然数の直角三角形の辺の比をa:b:cとした時、a,b,cの組をピタゴラス数と言います。

上図の3,4,5のほかにも、5,12,13や7,24,25などもピタゴラス数として知られています。


②と③は三角定規の形と同じです。30度、45度、60度とキリがいい角度が出てくる三角形です。こちらは辺の比に加え、角度まで合わせて覚えておきましょう。

三平方の定理(ピタゴラスの定理)の証明

三平方の定理(ピタゴラスの定理)を証明する方法は100以上あると言われています。今回は、直感的に一番わかりやすい証明を解説します。

辺の長さがa, b, cの直角三角形を以下の図のように4つ並べ、1辺の長さがa+bの大きい四角形を作ります。


外側の大きい四角形は4つの辺がa+bで角がすべて直角のため、正方形です。

次に、中にできる四角形の角度に注目してみましょう。


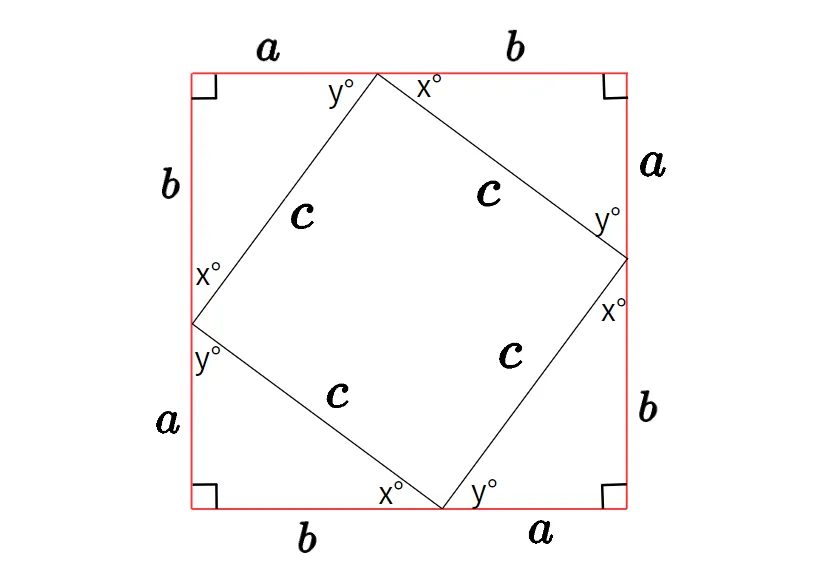
三平方の定理の証明1

1つの角は180-x-yとなり、これは三角形の内角の和が180度であることから90度となります。

つまり、中の四角形もすべての角が等しく、すべての辺の長さも等しいため、正方形であることがわかります。


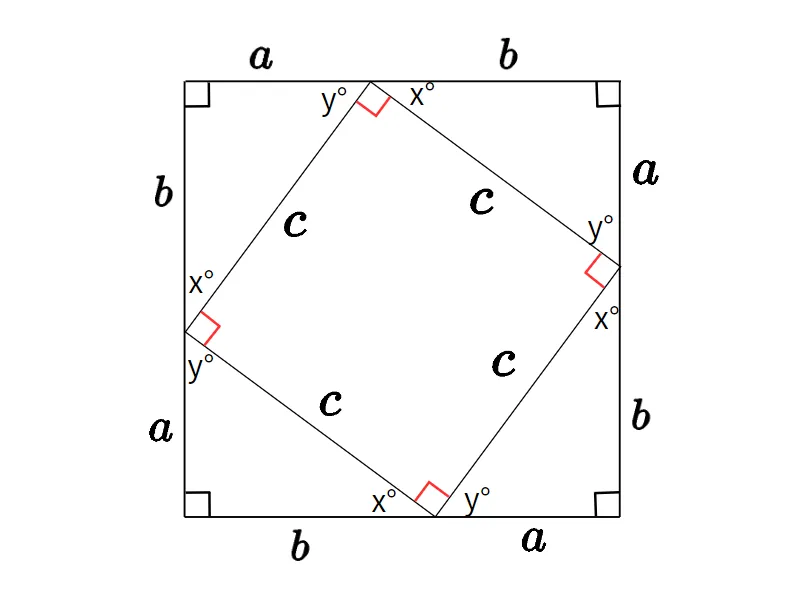
三平方の定理の証明2

ここで、中の正方形の面積を考えます。一辺の長さがcの正方形であるため、面積はc×cと計算できます。

ここで中の正方形は、大きい正方形から4つの直角三角形を引いても求められるため、以下の式が成り立ちます。

中の正方形の面積=大きい正方形の面積-4つの直角三角形


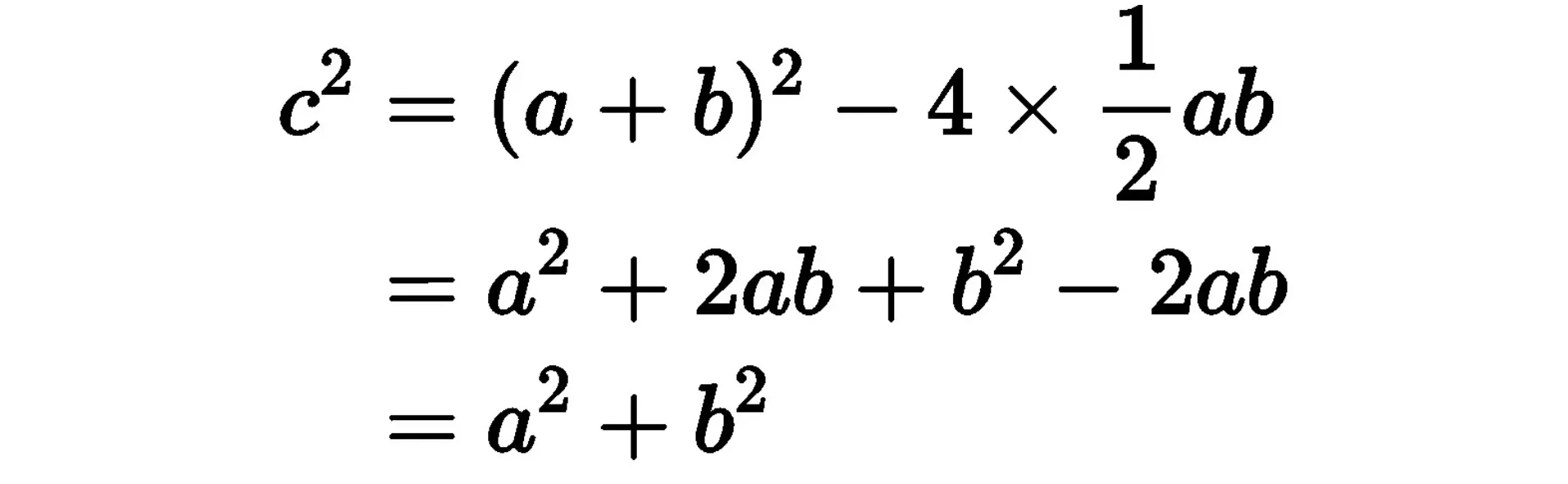
三平方の定理の証明3

以上から、三平方の定理の式を導けました。

練習問題

1. 直角三角形の一辺が 6 cm、もう一辺が 8 cm のとき、斜辺の長さを求めなさい


解答はこちら
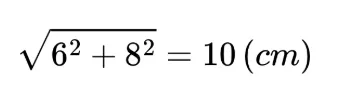
練習解答1

2. 次の三角形が直角三角形かどうか答えなさい
a. 5 cm, 12 cm, 13 cm
b. 2 cm, 3 cm, 4 cm


解答はこちら
練習解答2

3. 直角二等辺三角形の斜辺の長さが2の時、他の辺の長さを求めなさい


解答はこちら
練習解答3

4. もう1つの角が30°の直角三角形の斜辺の長さが3の時、他の辺の短い方の長さを求めなさい


解答はこちら
練習解答4

5. 平面上の点A(1, 2)と点B(6, 14)の距離を求めなさい


解答はこちら
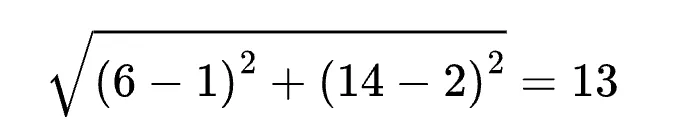
練習解答5

6. 1辺が10の正方形の対角線の長さを求めなさい


解答はこちら
練習解答6

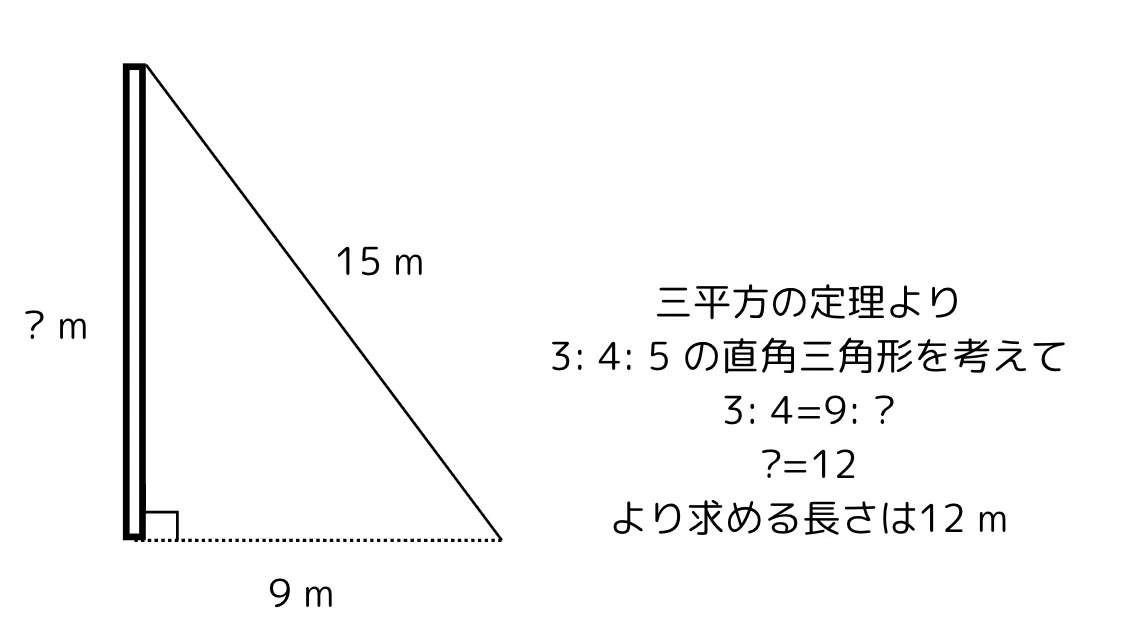
7. ある垂直に立つ鉄塔からロープを斜めに張ったところロープの長さは15mで、ロープの設置点から鉄塔までの距離が9mだった時、鉄塔の高さは何mか


解答はこちら
練習解答7

まとめ

三平方の定理（ピタゴラスの定理）は、数学において非常に重要な概念であり、図形の性質を理解するうえで欠かせないもので、もちろん受験にも必要不可欠です。

本記事では、定義から証明、頻出問題、実生活への応用例まで一貫して学べる構成にしました。図解と練習問題を活用しながら、理解を定着させてください。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

この記事を家族や友人に教える

明光プラスで読みたい記事のテーマを募集

明光プラスでは読者の方のご期待に沿えるように読みたい記事のテーマを募集しています。ぜひ下のリンクからアンケートにお答えください。

読みたい記事のテーマをリクエストする

関連タグ

#中学生 #数学

あわせて読みたい記事

タグ一覧

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

Home > 明光プラス > 学習 > 三平方の定理（ピタゴラスの定理）とは？計算の仕方と証明をやさしく解説！