2025.06.20

三角比(sin, cos, tan)とは？覚え方と三角比の表も紹介！

三角比ではsin(サイン),cos(コサイン),tan(タンジェント)やθ(シータ)といった聞きなれない呪文のような言葉がでてくるうえに、覚えることも多いため苦手意識を持っている方も多いのではないでしょうか。

そこでこの記事では、三角比の意味、覚え方を１からやさしく解説します。30°、45°、60°やそれ以外の角度の三角比の表も掲載しているので覚えるのに役立ててください。

三角比に続く三角関数についてはこちらの記事で詳しく紹介しています。三角比を理解した方はこちらの記事を合わせて参考にしてください。
三角関数（sin, cos, tan）入門！公式をわかりやすく覚える方法を紹介！

三角比とは？実は小学生のときに習ったことで理解できる！
基本的な三角比
sin(サイン)・cos(コサイン)・tan(タンジェント)とは？
三角比の拡張~単位円による定義~
覚えておくべき三角比の表
360度全て対応した三角比の表
練習問題
まとめ

三角比とは？実は小学生のときに習ったことで理解できる！

直角三角形には「直角以外のもう1つの角度がわかると三角形の辺の長さの比が決まる」という性質があります。

「なぜ？」と思うかもしれませんが、小学校の頃に習った「相似」でそのことはわかります。「2組の角がそれぞれ等しい」という相似条件は「直角三角形の直角ともう1つの角度がわかる」ということと同じことです。

例えば、ある直角三角形とそれに相似な直角三角形について考えてみましょう。

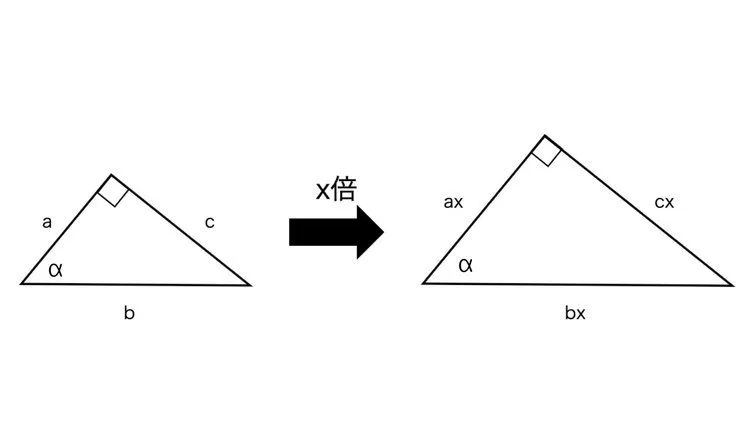
この2つの三角形は直角と角度αが同じなので、「2組の角度がそれぞれ等しい」という相似条件に当てはまります。

左の三角形の辺の比をa:b:cとすると、右の三角形の比はax:bx:cxとなります。xは正の実数であるため、xで割ると辺の比は左の三角形と同じa:b:cとなります。

つまり、直角三角形は直角以外のもう1つの角度が決まると辺の比は一定の値になることがわかります。この三角形の辺の比のことを三角比といいます。

基本的な三角比

三角定規で使われる30°, 45°, 60°が三角比の基本です。覚えておくのはもちろん、いつでも導出できるようにしておきましょう。

1つの角度が45度の直角三角形

わかりやすい45度の方から紹介します。

45度の場合は直角以外の角度が等しいため、直角二等辺三角形となります。

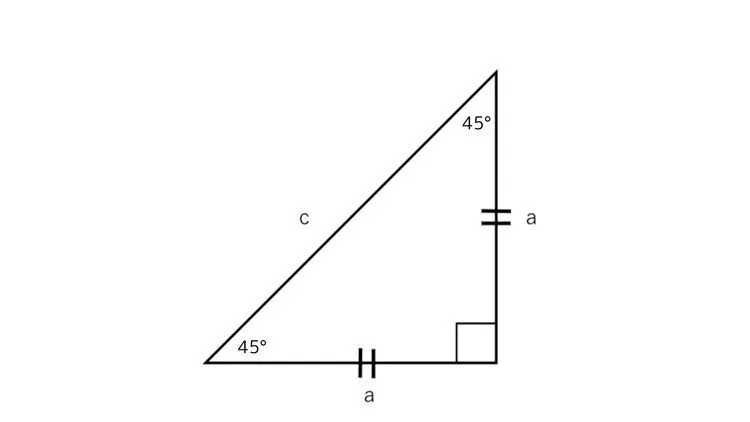
斜辺は三平方の定理から

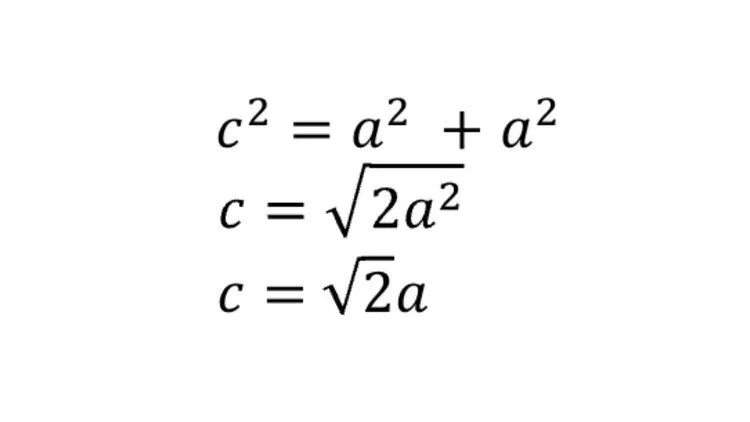
となり、a:c=1: $\sqrt{2}$ となります。

もう1つの角度が30度(60度)の直角三角形

正三角形の角から角度を二等分する線を引くと、対辺を直角に二等分する性質があることから、a:c=1:2となります。

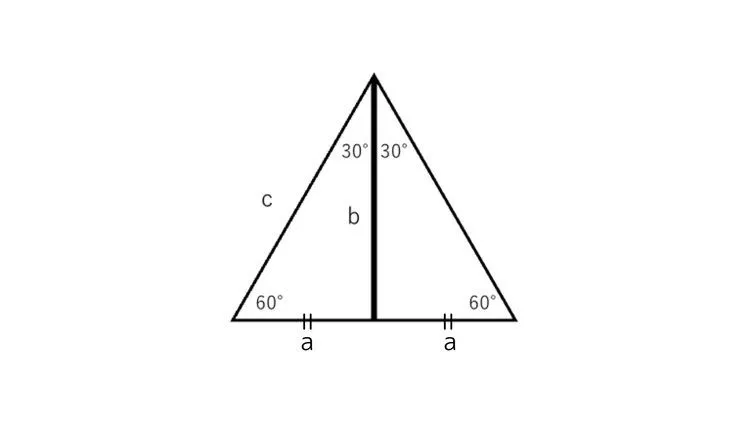
また、三平方の定理から

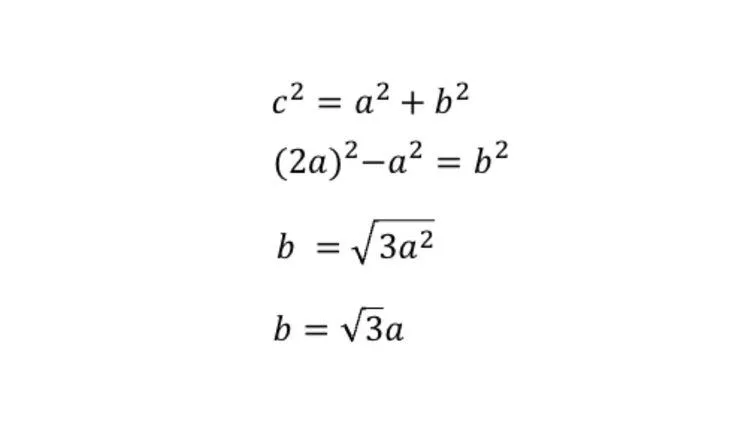
となり、a:b=1: $\sqrt{3}$ となります。よって、a:b:c=1: $\sqrt{3}$ :2と導けます。

この2つの有名な三角比は導けるようになることも重要ですが、スピーディに計算できるように暗記しておきましょう。

sin(サイン)・cos(コサイン)・tan(タンジェント)とは？

「三角比」と「有名な三角比」を理解したら、次はsin(サイン)・cos(コサイン)・tan(タンジェント)について学んでいきましょう。

有名な三角比を覚えておくと、ある辺の値がわかったらほかの辺の値をすぐに求めることができます。

60度をもつ直角三角形の斜辺の長さが1の場合、ほかの辺の長さを求めてみましょう。

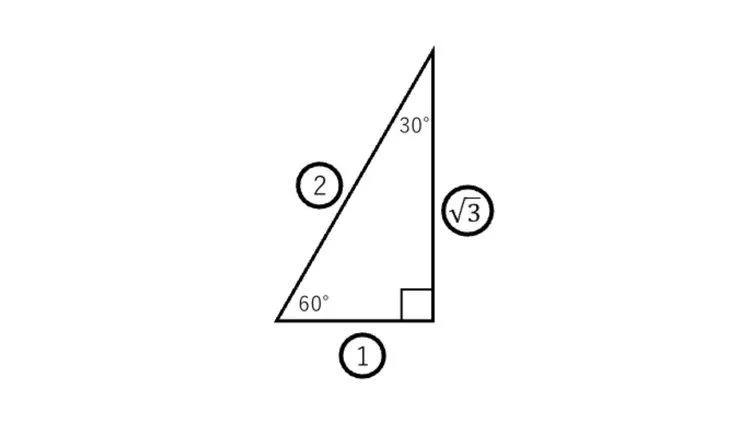
各辺の比を図に記入する際は実際の値と区別するために、○で囲って数字を書くことで、実際の値と比を区別しやすくなりわかりやすくなります。

sin(サイン)

斜辺が1の場合の対辺の長さを求めてみましょう。対辺は基準となる角と向かい合っている(基準となる角を端にもたない)辺のことをいいます。

斜辺と対辺の比は2: $\sqrt{3}$ でしたので、対辺の長さは $\sqrt{3}$ /2です。

このとき、基準とする角度を60度とし、対辺/斜辺とする比をsin(サイン)といいます。60度のときのsin比は $\sqrt{3}$ /2のため、sin60°= $\sqrt{3}$ /2とあらわします。

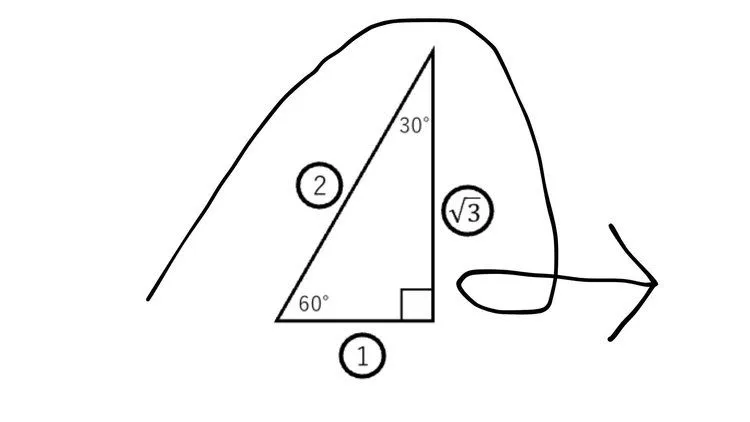
斜辺から対辺をなぞると筆記体のsのように見えませんか？sin(サイン)のsと覚えることがおすすめです。

※基準となる角度が左下、直角が右下のときsの形になりますが、鏡に反転したような直角三角形の場合はsも反転することに注意してください。

cos(コサイン)

斜辺が1の場合の隣辺の長さを求めてみましょう。隣辺は基準となる角と直角を両端にもつ辺のことをいいます。

斜辺と隣辺の比は2:1でしたので、隣辺の長さは1/2です。

このとき、基準とする角度を60°とし、その角を挟むように隣辺/斜辺とする比をcos(コサイン)といいます。60度のときのcos比は1/2のため、cos60°=1/2とあらわします。

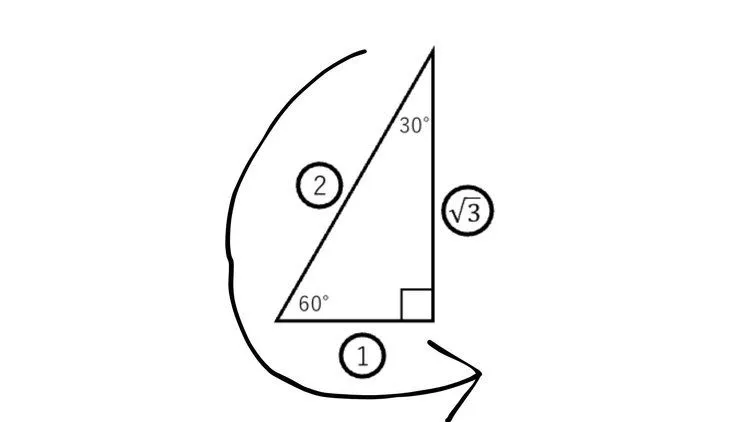
斜辺から隣辺をなぞるとcのように見えませんか？cos(コサイン)のcと覚えることがおすすめです。

※基準となる角度が左下、直角が右下のときcの形になりますが、鏡に反転したような直角三角形の場合はcも反転することに注意してください。

tan(タンジェント)

sin(サイン)・cos(コサイン)に続いて、最後にtan(タンジェント)を紹介します。

最後の組み合わせである隣辺と対辺の比がtan(タンジェント)となります。隣辺が1の場合の対辺の長さを求めてみましょう。

隣辺と対辺の比は1: $\sqrt{3}$ でしたので、対辺の長さは $\sqrt{3}$ です。このとき、基準とする角度を60度とし、斜辺/隣辺とする比をtan(タンジェント)といいます。60度のときのtan比は $\sqrt{3}$ のため、tan60°= $\sqrt{3}$ とあらわします。

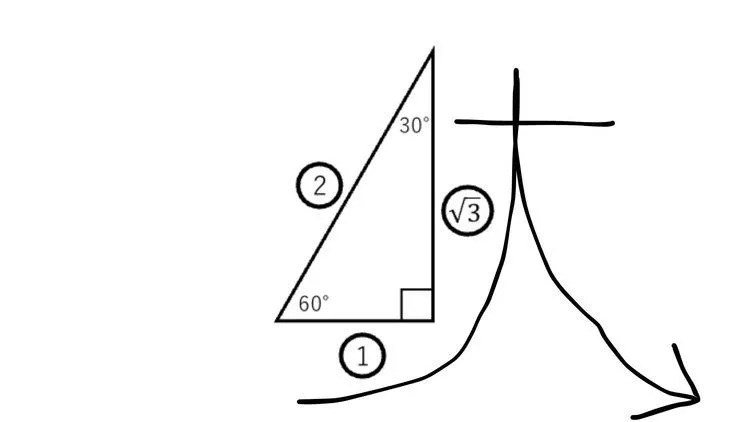
こちらも隣辺から対辺をなぞると筆記体のtのように見えませんか？tan(タンジェント)のtと覚えることがおすすめです。

※基準となる角度が左下、直角が右下のときtの形になりますが、鏡に反転したような直角三角形の場合はtも反転することに注意してください。

三角比の拡張~単位円による定義~

高校で習う三角比には90度以上のものが出てきます。三角形の内角の和は180度であるため、直角三角形以外で考える必要があり、生み出されたものが単位円による定義です。

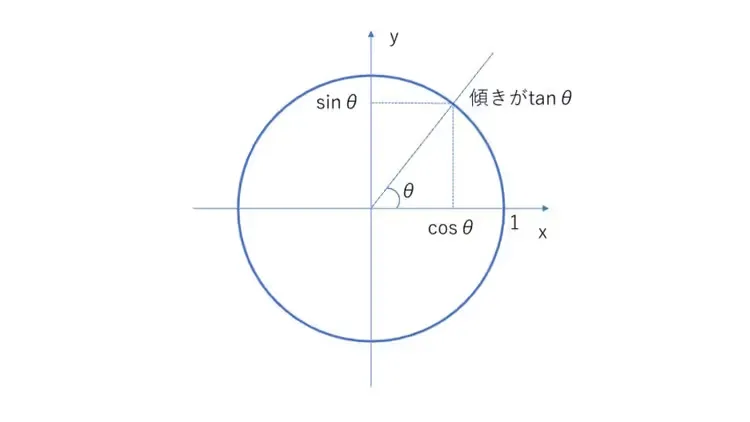
半径1の円をxy平面で考えると、原点からθの角度で半直線を引いたときに、半直線と円の交点ができます。その交点のyがsinθ、xがcosθ、傾きがtanθとするという定義です。

これにより90度以上の三角比について定義ができます。

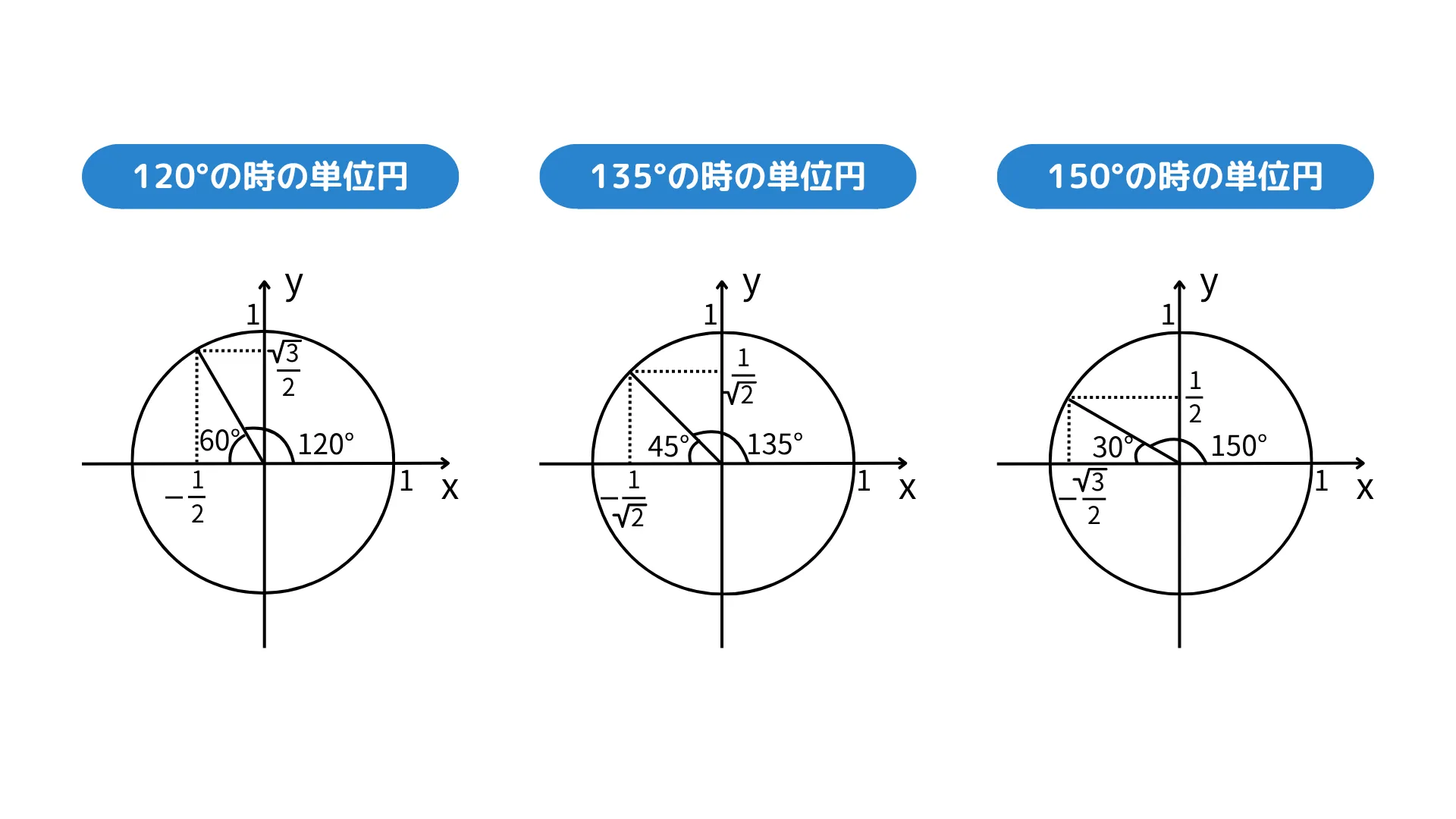
覚えておくべき三角比の表

単位円での定義から基本的な三角形の拡張により180°までの三角比を解説しました。

これらの三角比については覚えておくか素早く導出できるようにしておきましょう。

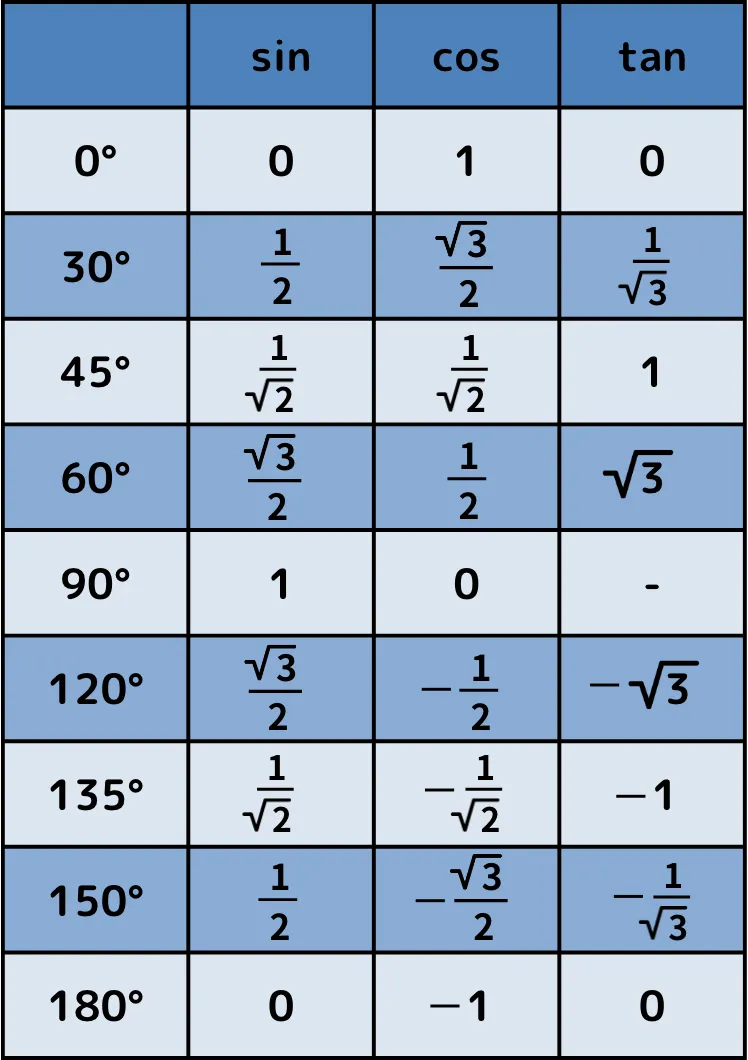
360度全て対応した三角比の表

有名な三角比以外を暗記することは現実的ではありません。

そのため、三角比の表が用意されていて、表を用いて計算することがあります。

そこで360度まで載っている三角比の表を用意しました。表の読み方を理解して、計算できるようになりましょう。

360度までわかる三角比の表はこちら

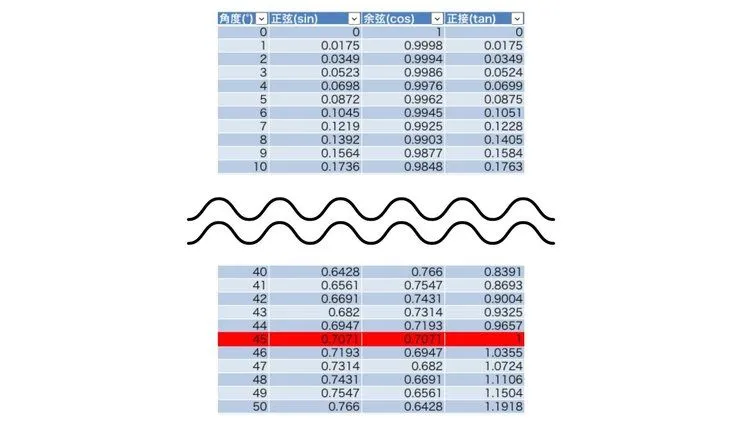
上の画像は三角比の表の一部です。sin45°の値を確認してみましょう。角度の列で45°になっているのは赤い枠で囲われた部分です。

その時の正弦(sin)の値は0.7071となっています。sin45°は1/ $\sqrt{2}$ でしたので、1/ $\sqrt{2}$ を変形すると1/ $\sqrt{2}$ = $\sqrt{2}$ /2≒1.4142/2=0.7071となり、表の値と一致していることが確認できます。

このように45°・30°・60°以外の場合でも表を用いて、自由に使いこなせるようにしましょう。

練習問題

次の値を求めなさい

1.sin30°

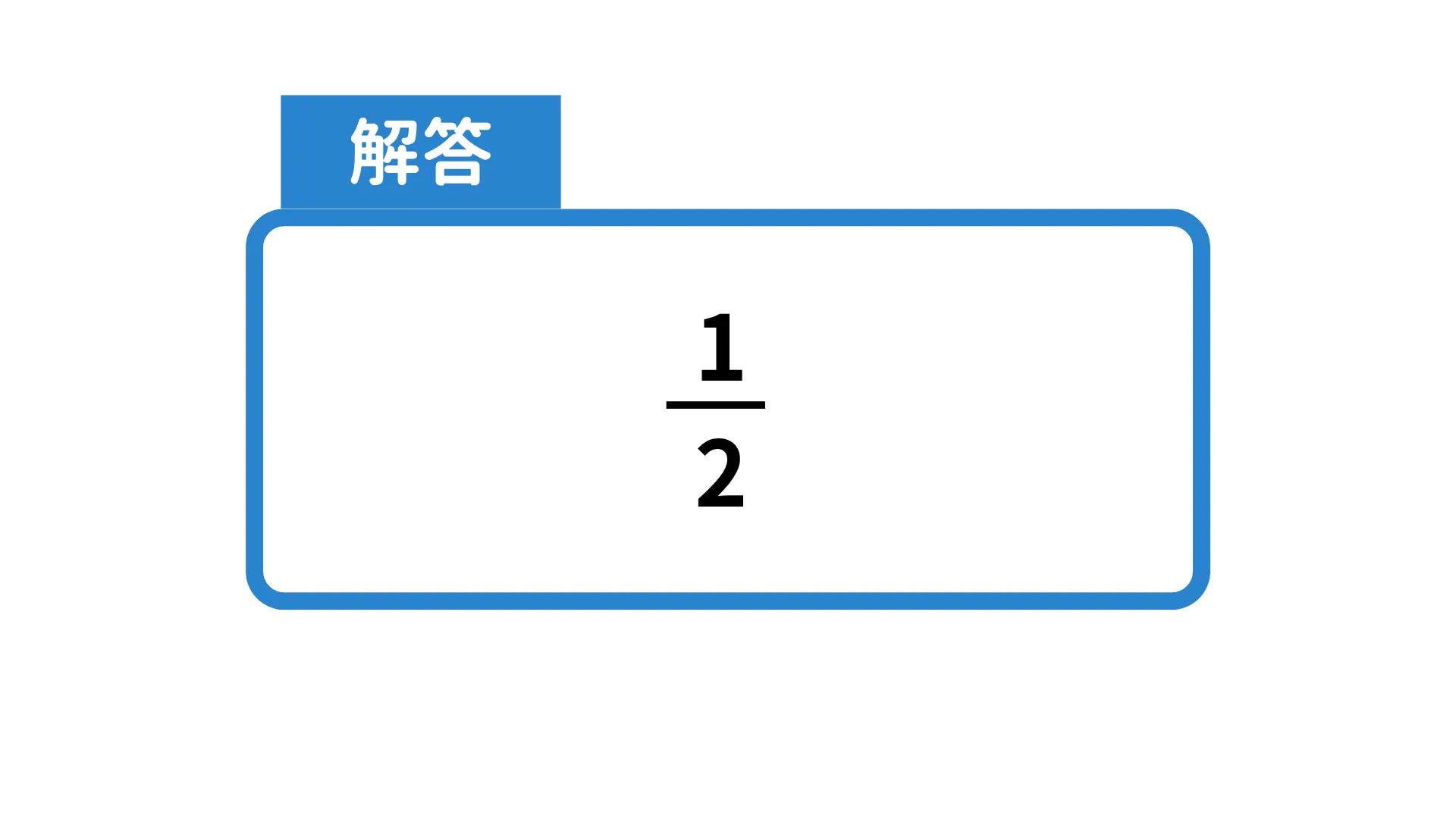
2.cos45°

3.tan60°

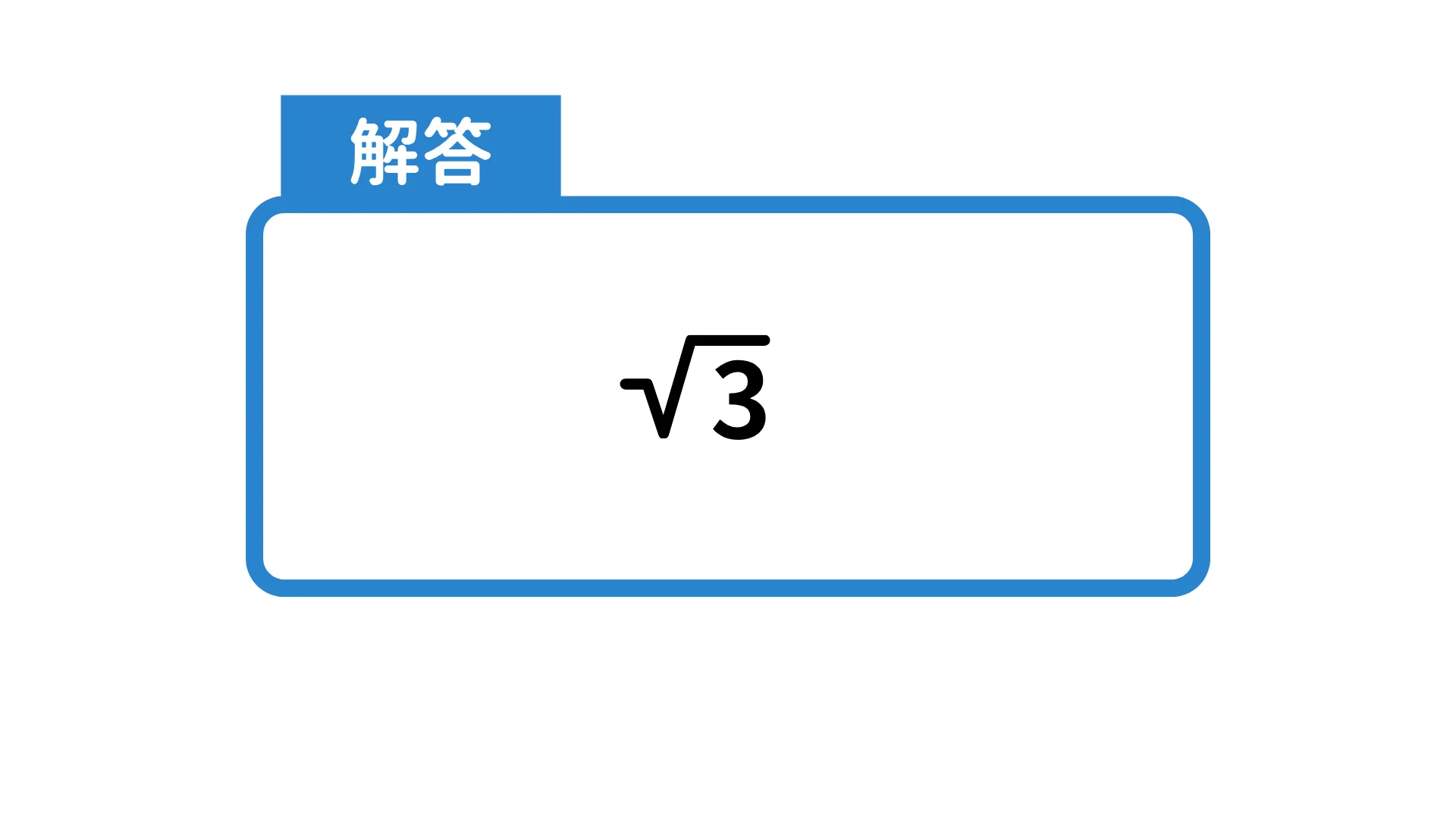
4.sin120°

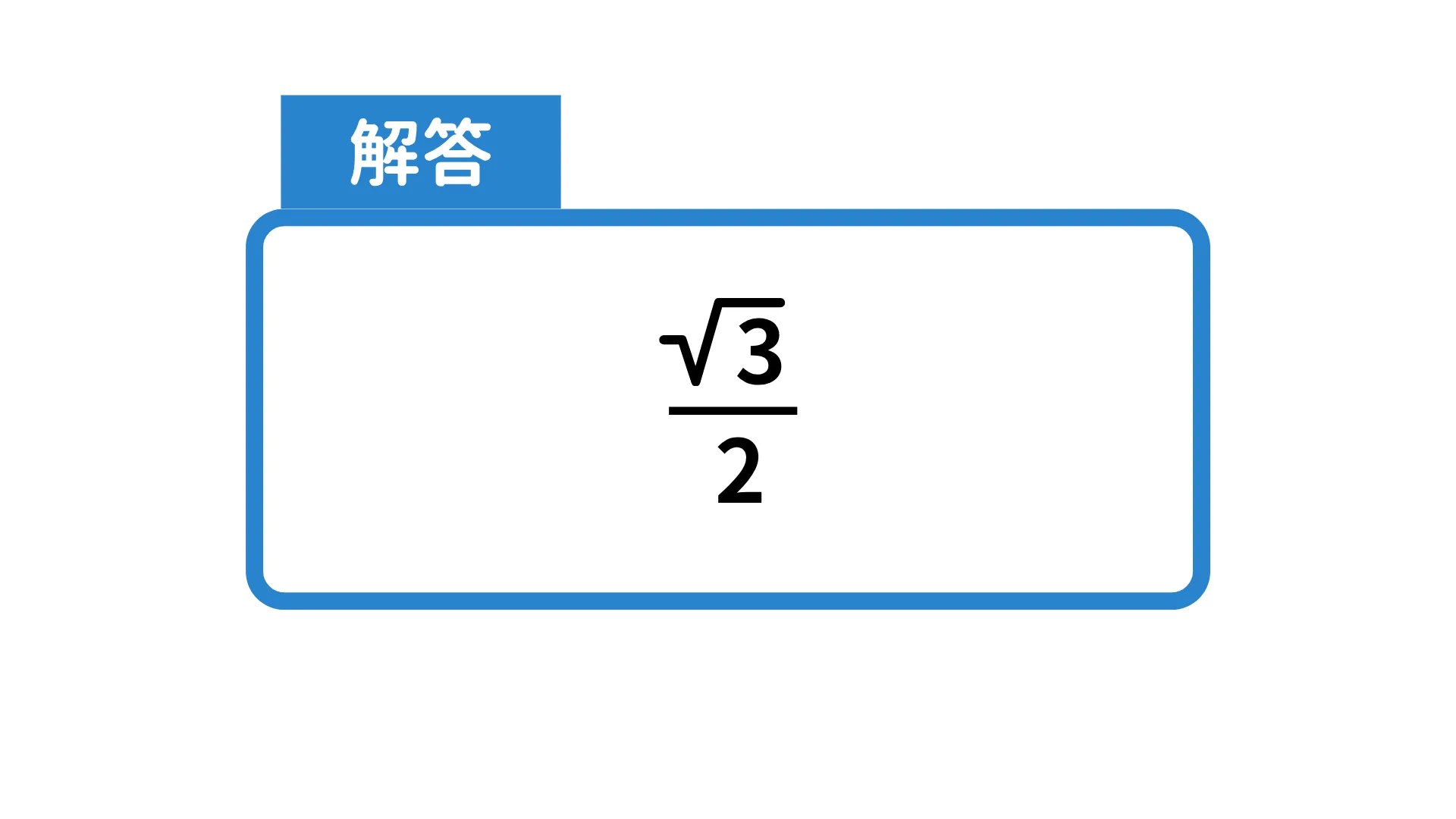
5.cos180°

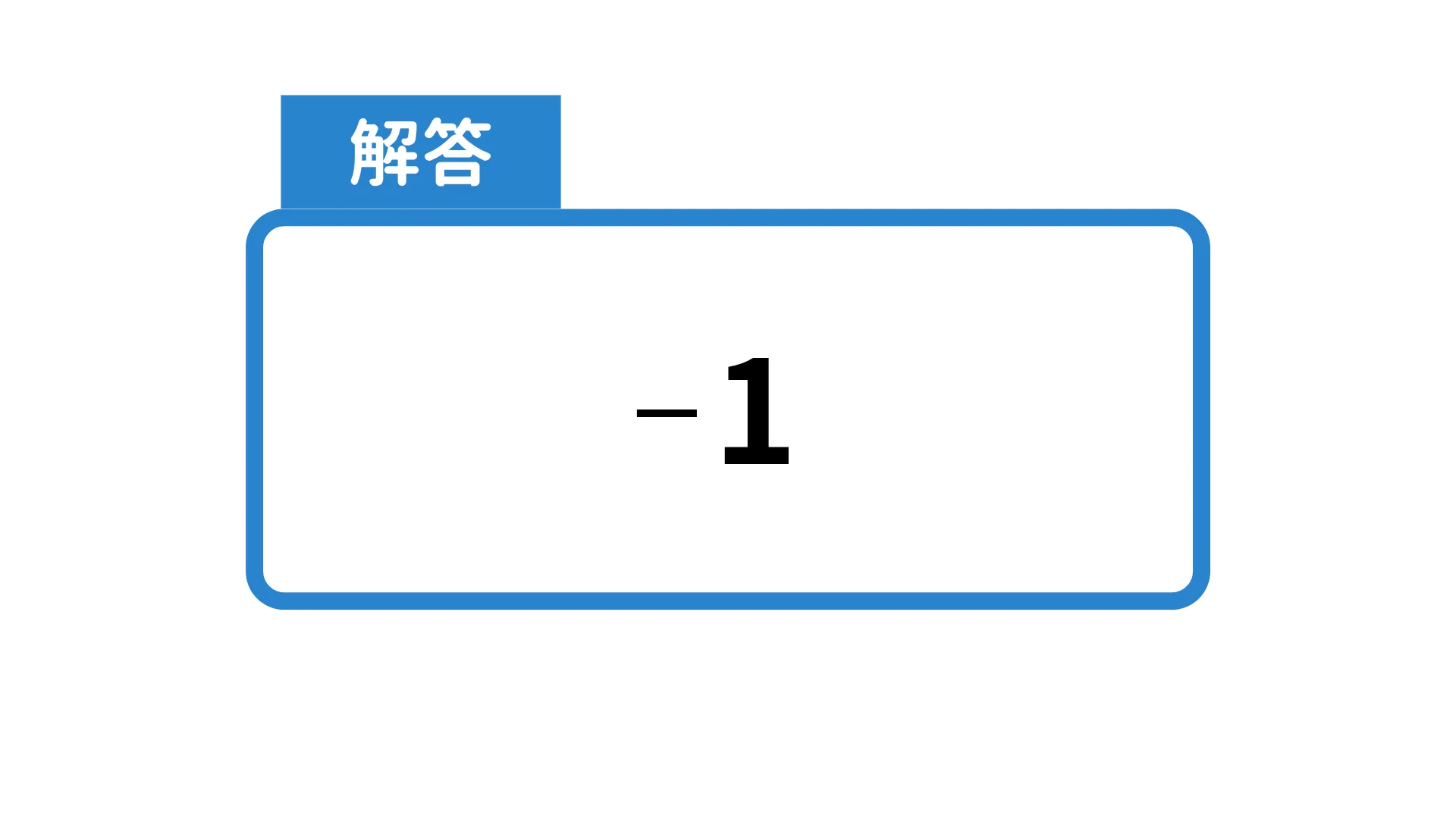
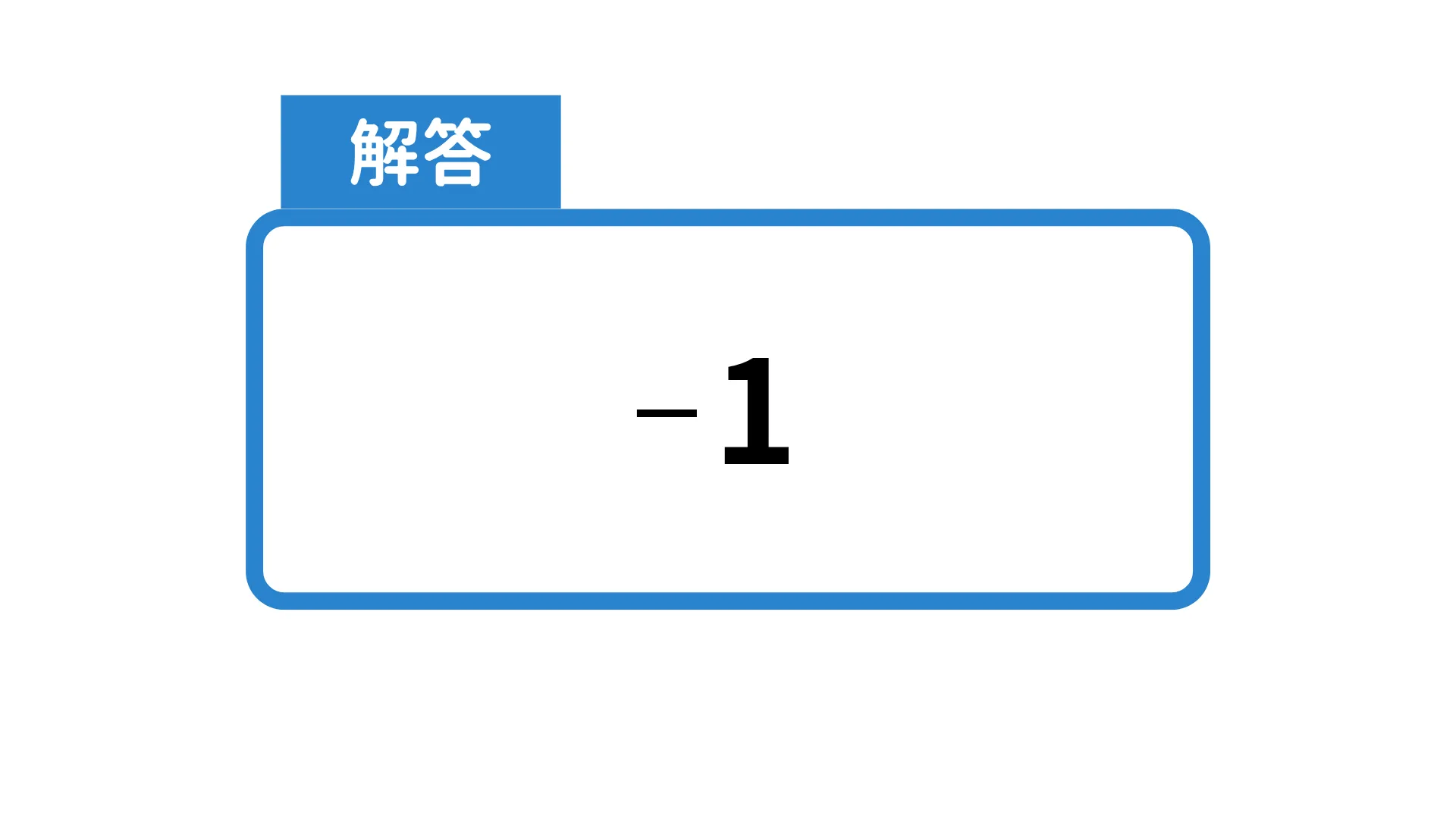
6.tan135°

三角比の表を用いて次の値を求めなさい

360度までわかる三角比の表はこちら

1.sin56°

2.cos78°

3.tan96°

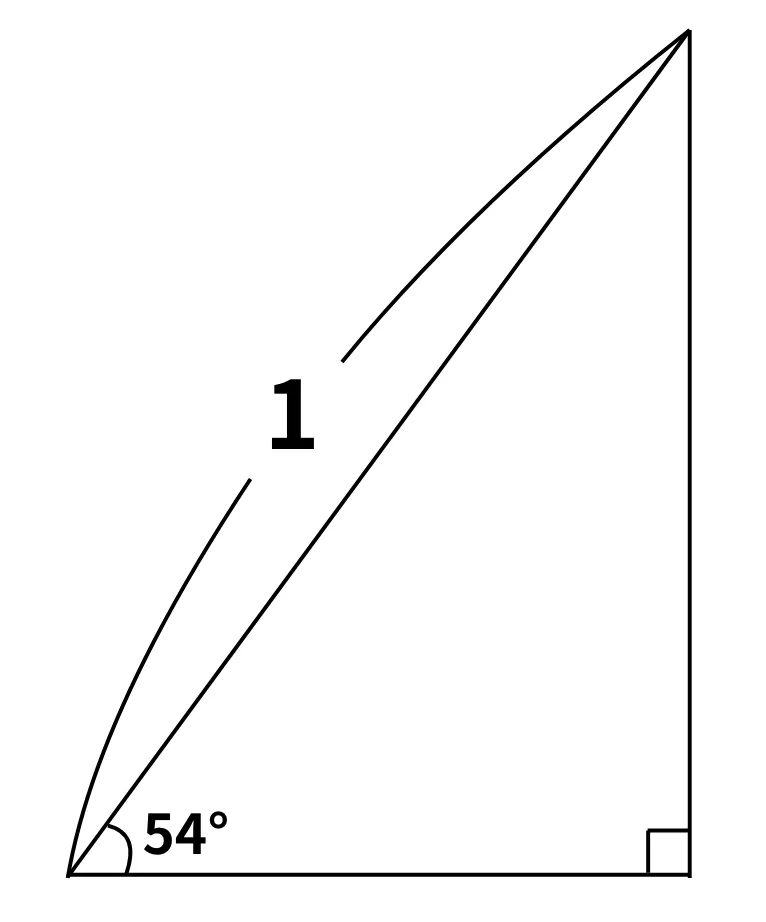
4.次の三角形のそれぞれの辺を求めなさい三角比15

まとめ

いかがでしたでしょうか。三角比について解説しました。

三角比は普段聞きなれない単語や覚えることが多いため、たくさんの方が苦手になりやすい単元ですが、続く単元の三角関数を理解するのに必須な単元です。

実は小学校の時に習った相似を使えば簡単に理解できる単元ですので難しい単語に惑わされず、三角比の導出方法を覚えてマスターできるようになりましょう。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

明光プラスで読みたい記事のテーマを募集

明光プラスでは読者の方のご期待に沿えるように読みたい記事のテーマを募集しています。ぜひ下のリンクからアンケートにお答えください。

読みたい記事のテーマをリクエストする

あわせて読みたい記事

微分とは？微分は○○です！定義・公式・使い方を解説

2025.07.07

高校数学の教育課程で避けては通れない微分。苦手に感じていたり、つまずいたりしてしまう方も多いのではないでしょうか。本記事では、微分とは何かという定義から、基本公式・実際の使い方・例題・応用までを、...
三角関数（sin, cos, tan）入門！公式をわかりやすく覚える方法を紹介！

2025.06.26

三角関数では$\sin$(サイン),$\cos$(コサイン),$\tan$(タンジェント)や$\theta$(シータ)といった聞きなれない呪文のような言葉が多く出てくるのに加え、覚える公式が多いため...
等比数列は簡単！一般項や和の公式を1から解説します

2025.06.06

数Bの数列を学習すると等差数列の次に学ぶのが等比数列です。しかし等比数列に比べて見た目が複雑で規則性も掴みにくいため、苦手意識を持っている人も多いのではないでしょうか。等比数列は漸化式の問題を解くと...