2025.06.20

分数の掛け算のやり方を1からわかりやすく解説します！

小学5年生頃から習う分数の掛け算、一見単純そうですがいろいろなパターンがあり苦手とするお子さまも多いのではないでしょうか。

そこでこの記事では、分数とは何かというところから、分数の掛け算のやり方を1からわかりやすく解説します。

分数とは？

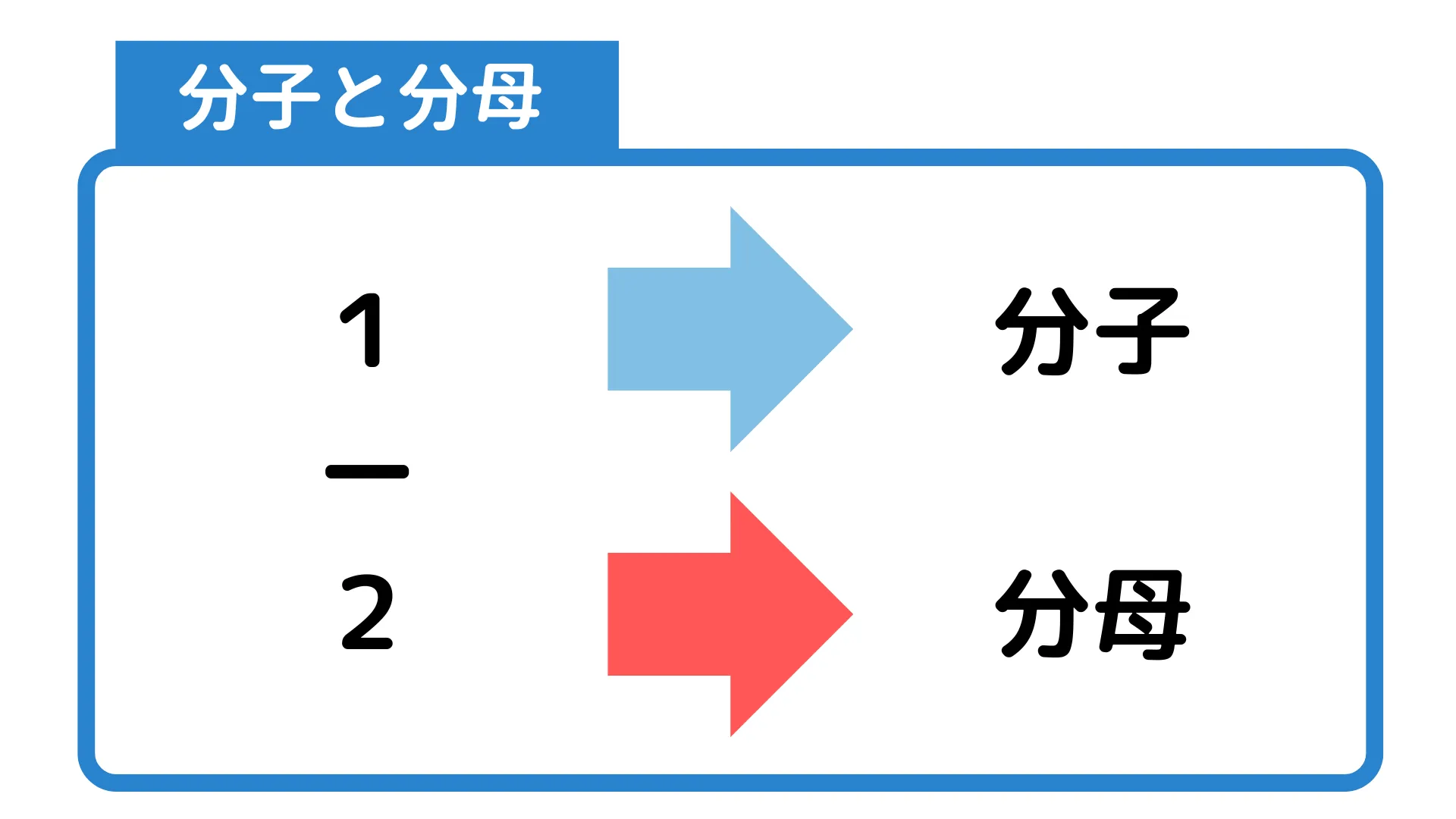
分数は整数同士の割り算を表したものです。
例えば$\frac{1}{2}$は1を2で割ったもので、$\frac{3}{5}$は3を5で割ったものです。

ここで割られる数を「分子」といい、分数の上に書きます。また、割る数は「分母」といい、分数の下に書きます。

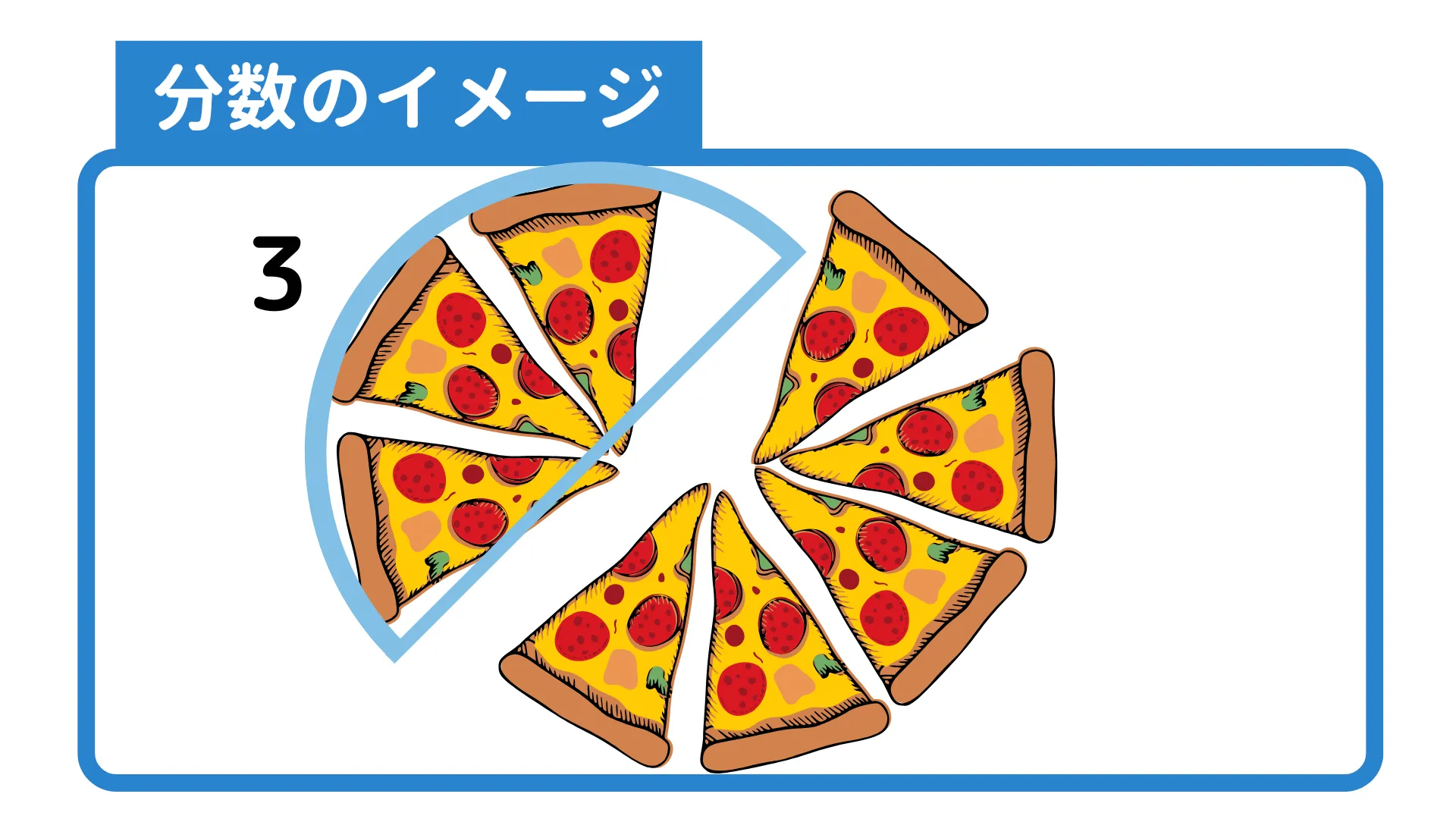
分数は分母の数で分けたうちの分子分とイメージすることができます。
例えば$\frac{3}{8}$はピザを8枚に切り分けたうちの3つ分です。

また分数は小数より掛け算がしやすい場合が多く、分数の掛け算になれておくことで計算のスピードが上がります。

分数の掛け算のやり方

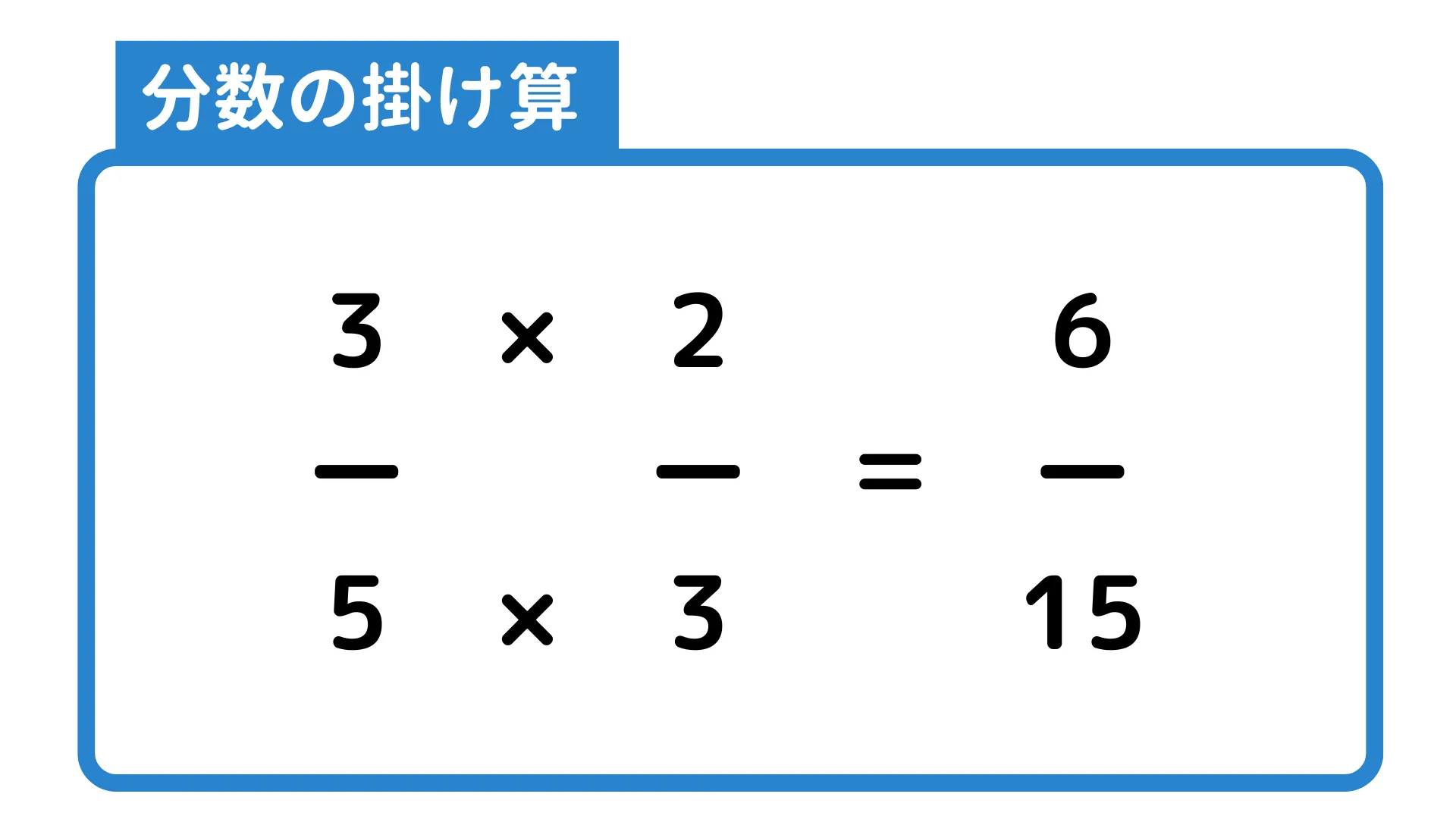
分数の掛け算のやり方は基本的に「分子同士を掛け算したもの÷分母同士を掛け算したもの」です。

なぜそうなるかは分数の定義から考えられます。

例えば$\frac{3}{5}\times\frac{2}{3}$という式は3÷5×2÷3と表すことができ、並び替えると3×2÷5÷3と書き換えられます。
割られる数（分子）が3×2になり、割る数（分母）は5×3になることがわかります。

なぜ分母が5×3と割る数の掛け算になるの？と思うかもしれませんが、簡単な例で確認してみましょう。

なぜ分母も掛け算なのか

同様にピザを分けることで考えてみましょう。
1枚のピザを2つに分けたときの1ピースは$\frac{1}{2}$です。

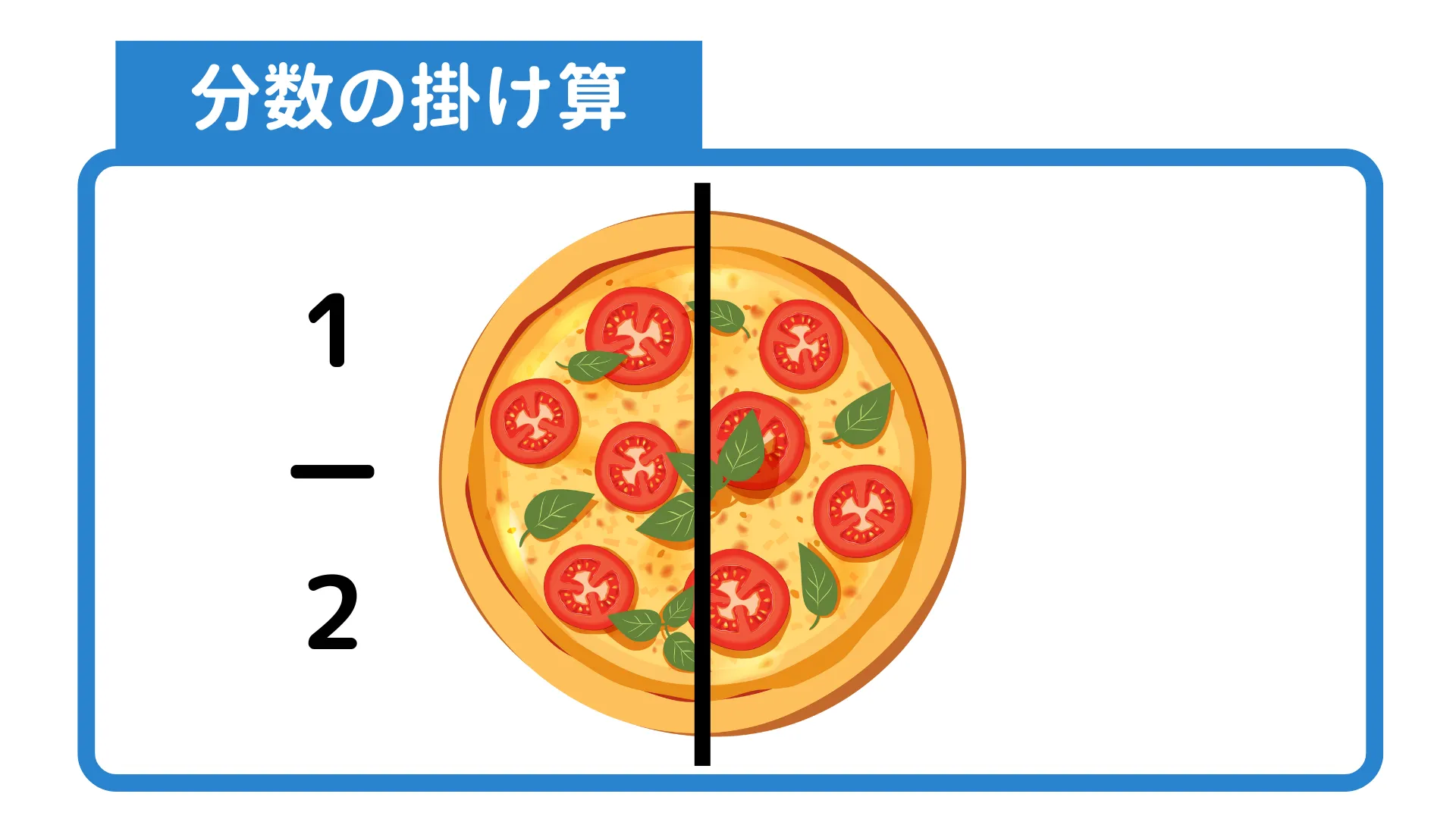
さらにこのピースを2つに分けることを考えます。

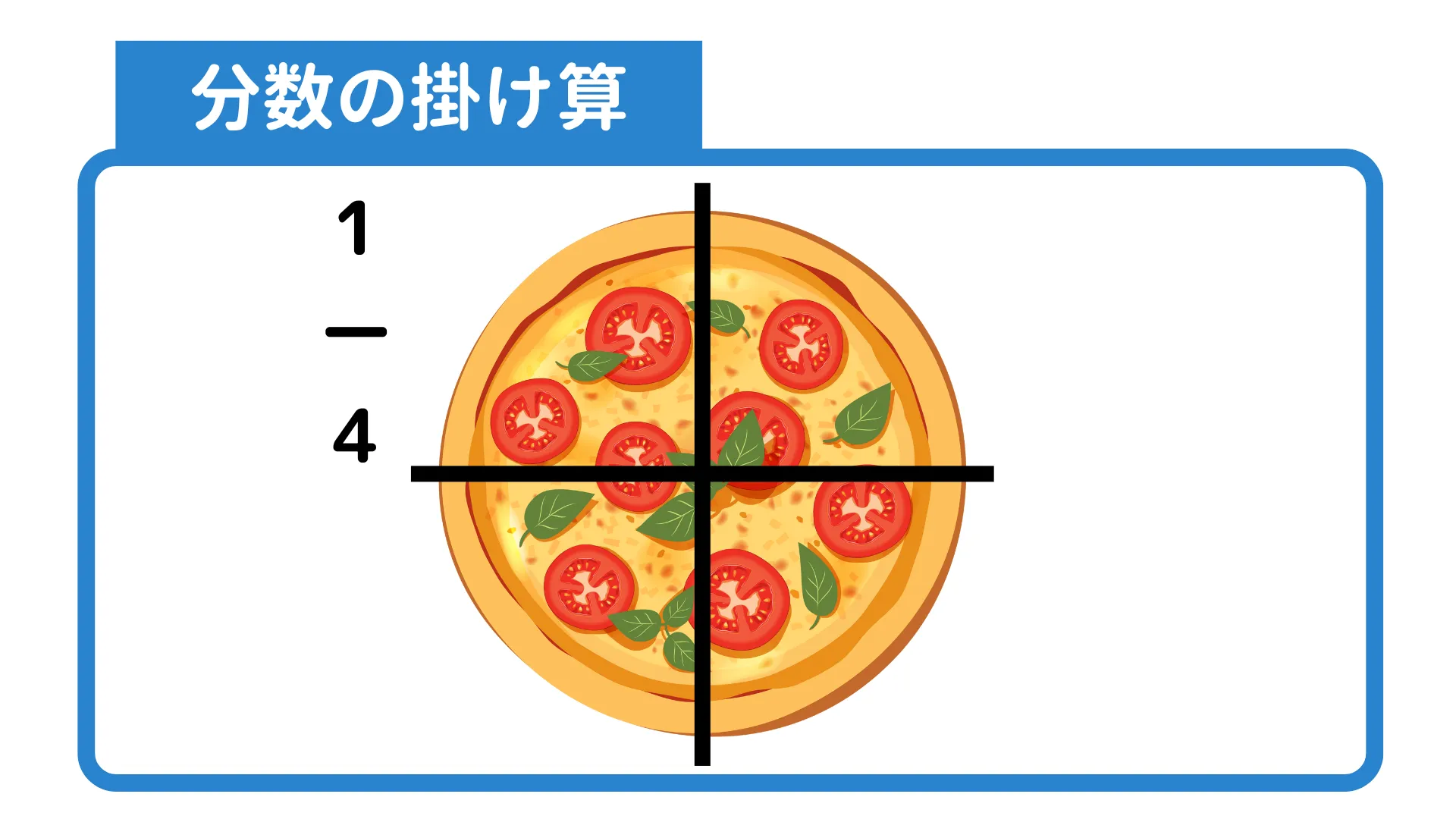
結果ピザが4等分されていて割る数をかけた2×2=4ピースになることがわかり、割る数である分母は掛け算になることが理解できます。

パターン別分数の掛け算のやり方

分数には「帯分数」という形があり、また、帯分数と分数、整数と分数の掛け算など、いろいろなパターンがあります。それぞれのやり方を解説します。

帯分数が入った分数の掛け算のやり方

分数の中には帯分数という整数部分と分数部分で表されるものがあります。
例えば$1\frac{1}{3}$という帯分数は＋が省略されている$1+\frac{1}{3}$と同じ意味です。

$1\frac{1}{3}×\frac{1}{2}$のように帯分数が入った掛け算の場合は帯分数を仮分数に直してから計算すると混乱が生じにくく計算もしやすいです。
仮分数というのは分子のほうが分母より大きい分数のことです。

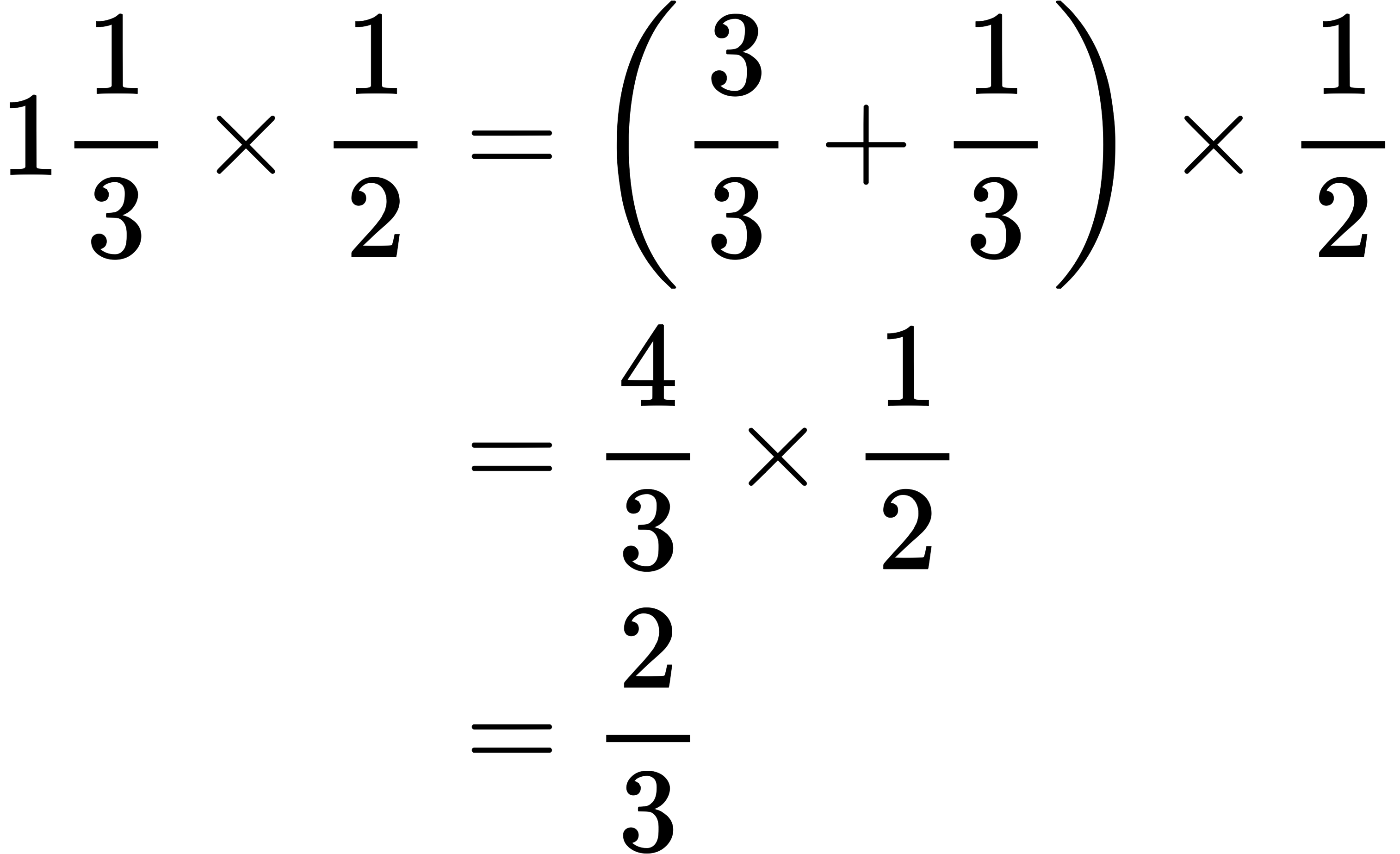
整数と分数の掛け算

整数と分数の掛け算も、整数を分母が1の分数と考えると簡単です。
例えば$3×\frac{5}{9}$は以下のように考えることができます。

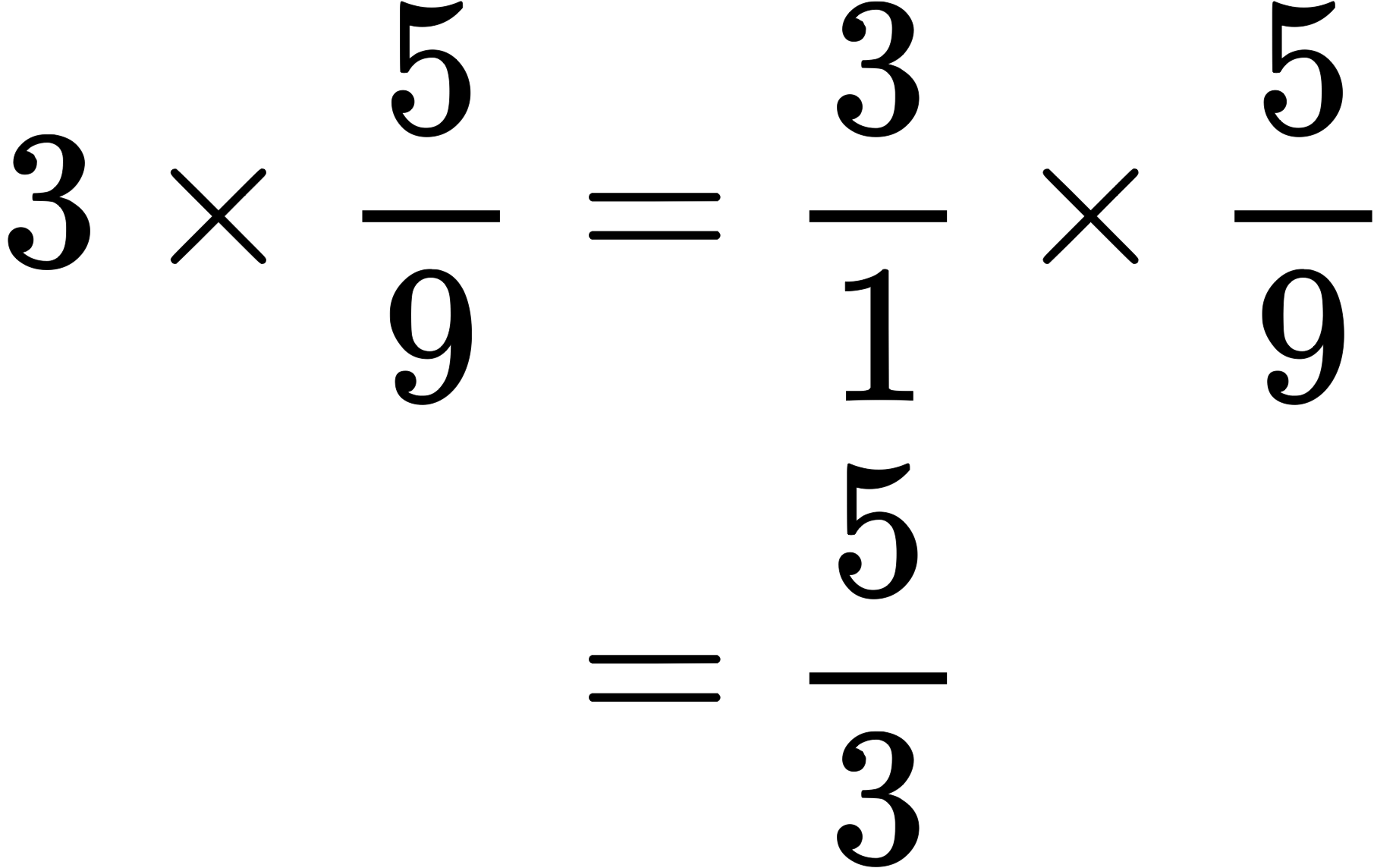
このイメージができていればいちいち整数を分数に直さなくても計算できるようになります。

分数の掛け算のテクニック

分数の掛け算をするときには必ず約分がまずできるかを確認しましょう。

例えば$\frac{12}{36}\times\frac{45}{90}$という計算をそのまま分子同士、分母同士の掛け算をするのは大変です。
しかし各項は約分でき、$\frac{1}{3}\times\frac{1}{2}$と簡単な分数の掛け算にすることができます。

しかもこの約分のテクニックは各分数での約分だけでなくお互いの分母分子で行うこともできます。

例えば$\frac{7}{12}\times\frac{3}{14}$という計算ではこのように約分ができます。

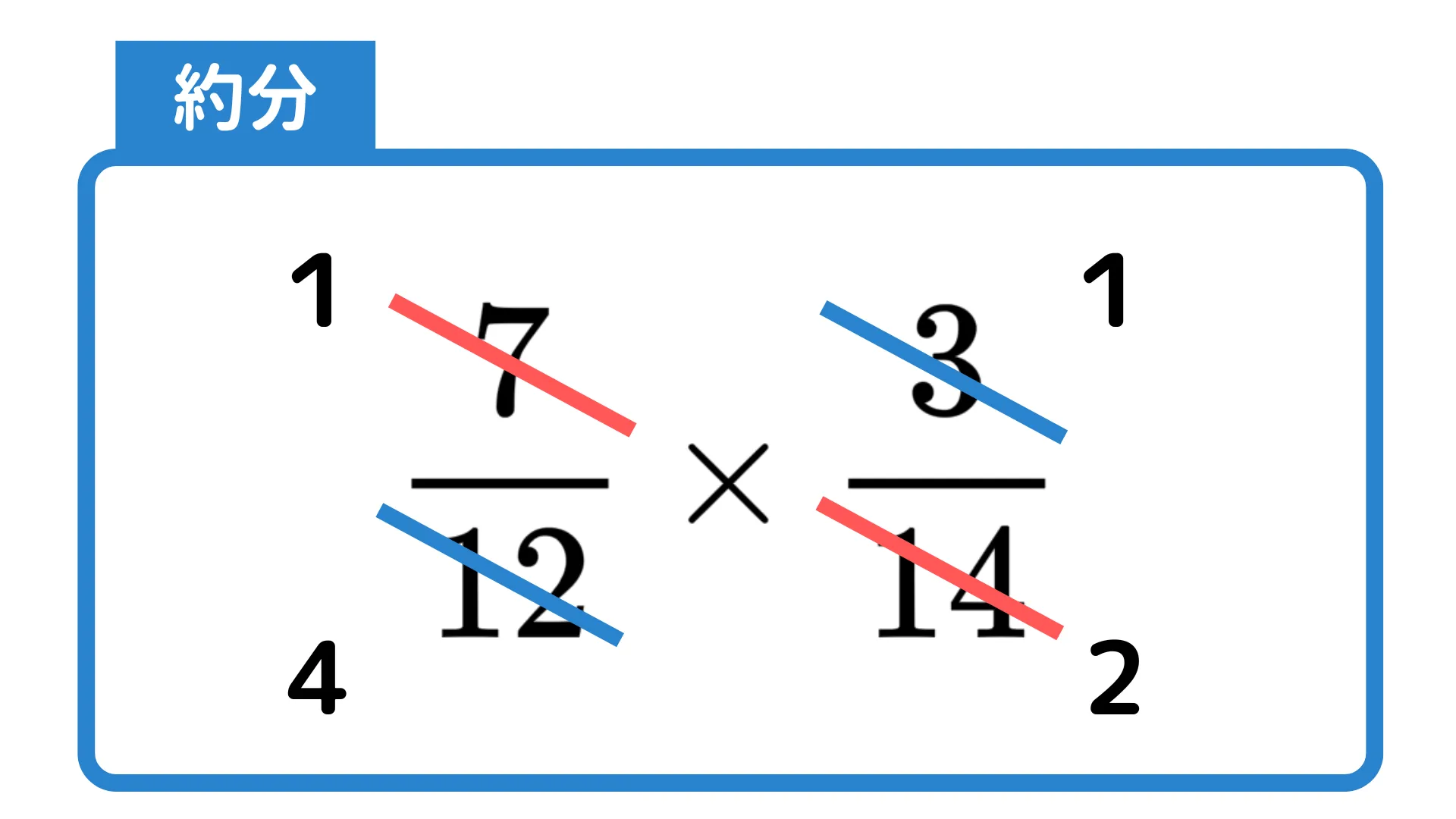
分数の計算で複雑になりそうな場合は、まず約分できるかどうかを確認する習慣をつけておくことが、ミスを減らすうえでも大切です。

分数の掛け算の練習問題

$\frac{1}{2}\times\frac{3}{5}$ を求めよ

解答はこちら

$1\frac{2}{3}×\frac{2}{5}$を求めよ

解答はこちら

$3 \times \frac{4}{19} $を求めよ

解答はこちら

$\frac{12}{24}\times\frac{15}{25}$を求めよ

解答はこちら

$1\;\mathrm{cm}^3$で$\frac{2}{5}\,\mathrm{g}$の木材があります。この木材を$\frac{12}{5}\,\mathrm{cm}^3$集めると重さは何gでしょう。

解答はこちら

まとめ

いかがでしたでしょうか。本記事では、分数の掛け算の基本から帯分数・整数との計算、そして約分のテクニックまで解説しました。

分数とは「割り算を表す記号」という本質をつかむことで計算がスムーズになり、約分を先に行えばミスも大幅に減らせます。練習問題を繰り返し解いて、ミスなくさまざまな計算に慣れましょう。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

明光プラスで読みたい記事のテーマを募集

明光プラスでは読者の方のご期待に沿えるように読みたい記事のテーマを募集しています。ぜひ下のリンクからアンケートにお答えください。

読みたい記事のテーマをリクエストする

あわせて読みたい記事

三角形の面積の求め方！学齢に応じた公式の一覧となぜそうなるのかを解説します

2025.06.04

三角形の面積を求める問題は小学生から習いますが、大学入試に至るまでいろいろな求め方を習います。場合によって使い分ける必要がありますが、全てを完全に理解している方は少ないのではないでしょうか。本記事...
パーセントの計算の仕方は？割合や歩合と合わせて1からわかりやすく解説！

2024.10.15

パーセントや割合は実生活でもよく使われる表現で、計算の仕方の理解やある程度の暗算ができることが好ましいです。この記事ではパーセントの計算や割合の計算をどのようにすればいいのか理解できていない方やパ...
円周率の定義とは？簡易的な求め方も合わせて簡単に解説！

2024.09.06

円周率は小学5年生で初めて習いますが、大学入試でも円周率に関係する問題はよく出てきます。小学生で覚えておく円周率はだいたい3.14までですが、3.14以下も無限に続くことが知られています。単純なよ...