明光義塾へ
学習

2025.01.22     

積分とは○○です！積分を最初からやさしく解説し、覚えるべき公式を紹介！

積分サムネ.png

高校数学の教育課程で避けては通れない積分。微分と同様に苦手に感じていたり、つまずいたりしてしまう方も多いのではないでしょうか。

そこで本記事では、積分とは一体何なのかをわかりやすくかみ砕いて紹介し、積分の覚えるべき公式を一覧に紹介し、練習問題と合わせてやさしく解説します。

積分を理解するためにはまず微分の理解が必須です。微分についてはこちらの記事で詳しく紹介しているため微分を理解していない方はこちらを先に読むことをおすすめします。
微分とは一体何なのか？微分はただの○○です！

もくじ

積分とは？

積分は微分の反対のことです。また、積分は関数のある範囲の面積を求める方法になります。積分には範囲を指定して具体的な面積を求める「定積分」と範囲を指定しない「不定積分」の2つに分かれます。

定積分より不定積分のほうが範囲が指定されていない広義の積分なので、この記事では不定積分をメインに紹介し、必要に応じて定積分の紹介をしていきます。

積分の式は次のように表されます。

定積分

\begin{aligned} \int_a^b f(x)dx &=[F(x)]_a^b\\ &=F(b)-F(a) \end{aligned}

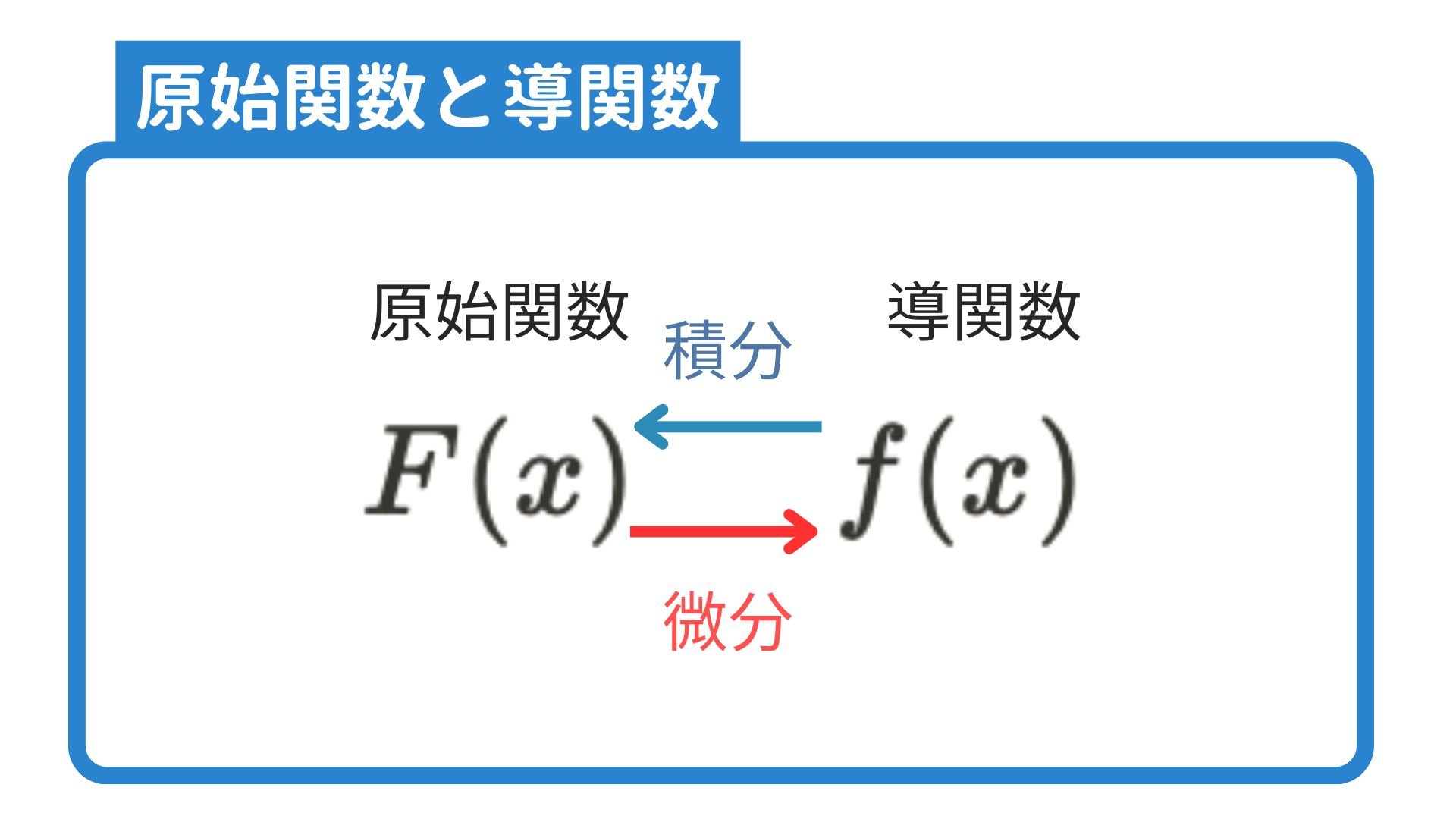
ただし$F(x)$は微分すると$f(x)$になる関数で原始関数と呼び、反対に$f(x)$は$F(x)$の導関数と呼びます。

積分1

不定積分

\begin{aligned} \int f(x)dx=F(x)+C \end{aligned}

不定積分の最後についているCは積分定数と呼びます。

定数は微分すると0になります。そのため、積分する際、もともとの式には定数があったのかどうかわからないため、定数を積分定数Cという文字で表現します。

定積分と不定積分、また積分定数についての直感的な説明は後ほどしますが、まず積分がなぜ面積を求めることになるのかを説明します。

なぜ関数の面積を求めることが積分になるのか

微分の反対が面積を求める方法と言われてもピンと来ないことでしょう。ではなぜ積分が面積を求めることになるのかをまず説明していきます。

$y=f(x)$と$x=0, x=t,x$軸の直線で囲まれた面積を$S(t)$と置きます。

$t$を微小な$\Delta t$だけ大きくした際の$S(t+\Delta t)$がどれくらい変化するかを考えます。

積分2

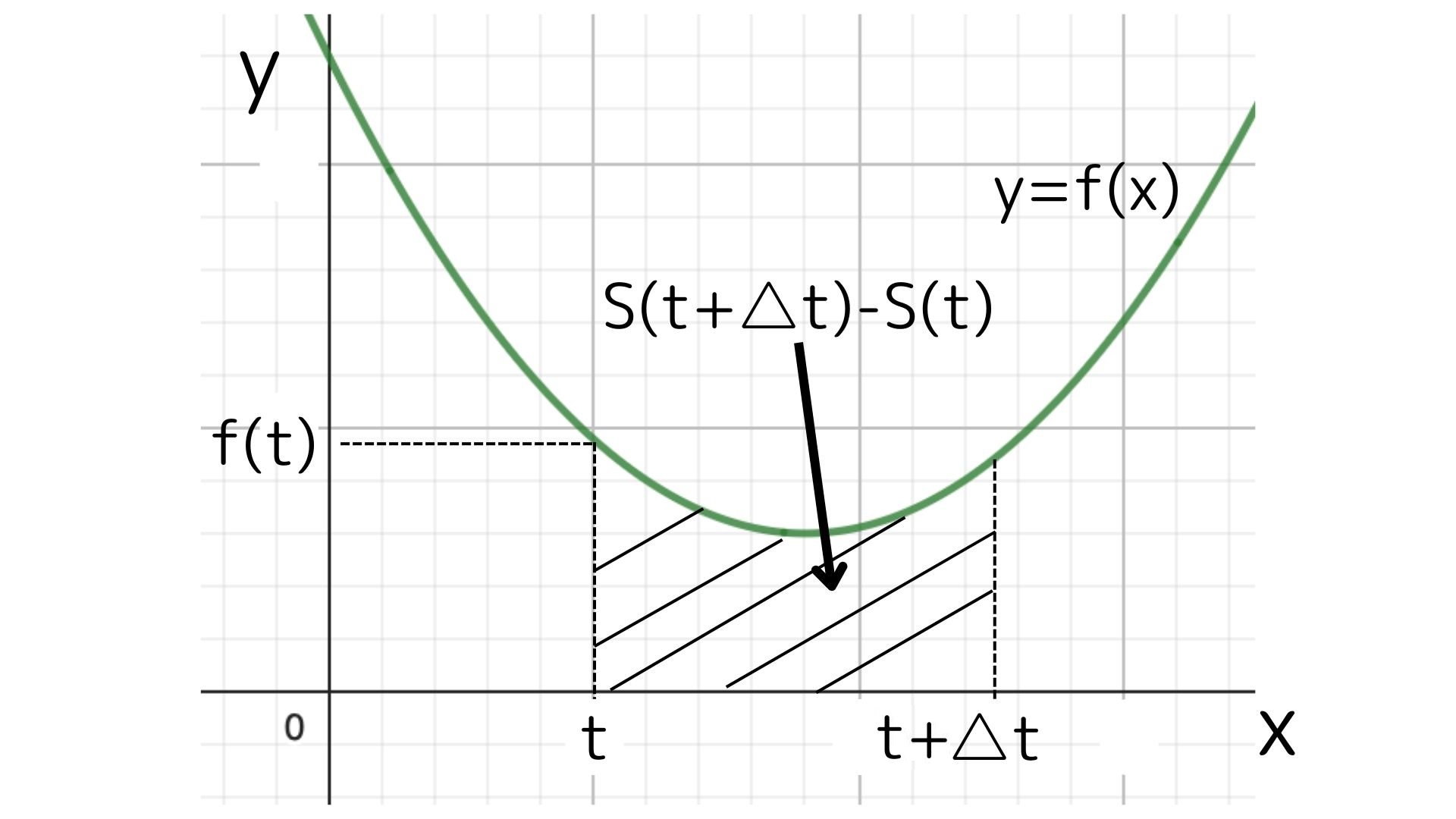
この場合に$Δt$が微小であれば網掛けの部分の高さは$f(t)$、横は$\Delta t$とすることができます。つまり次の等式が成り立ちます。

\begin{aligned} \ S(t+\Delta t) - S(t) = f(t)×Δt \end{aligned}

両辺を$\Delta t$で割ると

\begin{aligned} \frac{S(t+\Delta t) - S(t)}{\Delta t} = f(t) \end{aligned}

となり、$\Delta t→0$と極限を取ると微分の形になります。

\begin{aligned} \lim_{\Delta t→0} \frac{S(t+\Delta t) - S(t)}{\Delta t} = f(t) \end{aligned}

つまり面積の$S(x)$の微分は$f(x)$となり、また面積を求める$S(x)$は$f(x)$の微分の反対であるということが言えます。微分の反対が積分となります。よって、関数の面積を求めることを積分と呼ぶのです。

定積分と不定積分、積分定数を直感的に説明します

微分の記事で説明しましたが、代表的な微分の説明の仕方に距離と速さの説明がありました。

$x$軸に時間と$y$軸に進んだ距離を記したグラフを微分すると速さが求められるという内容です。まずここに速さのグラフを示します。

積分3

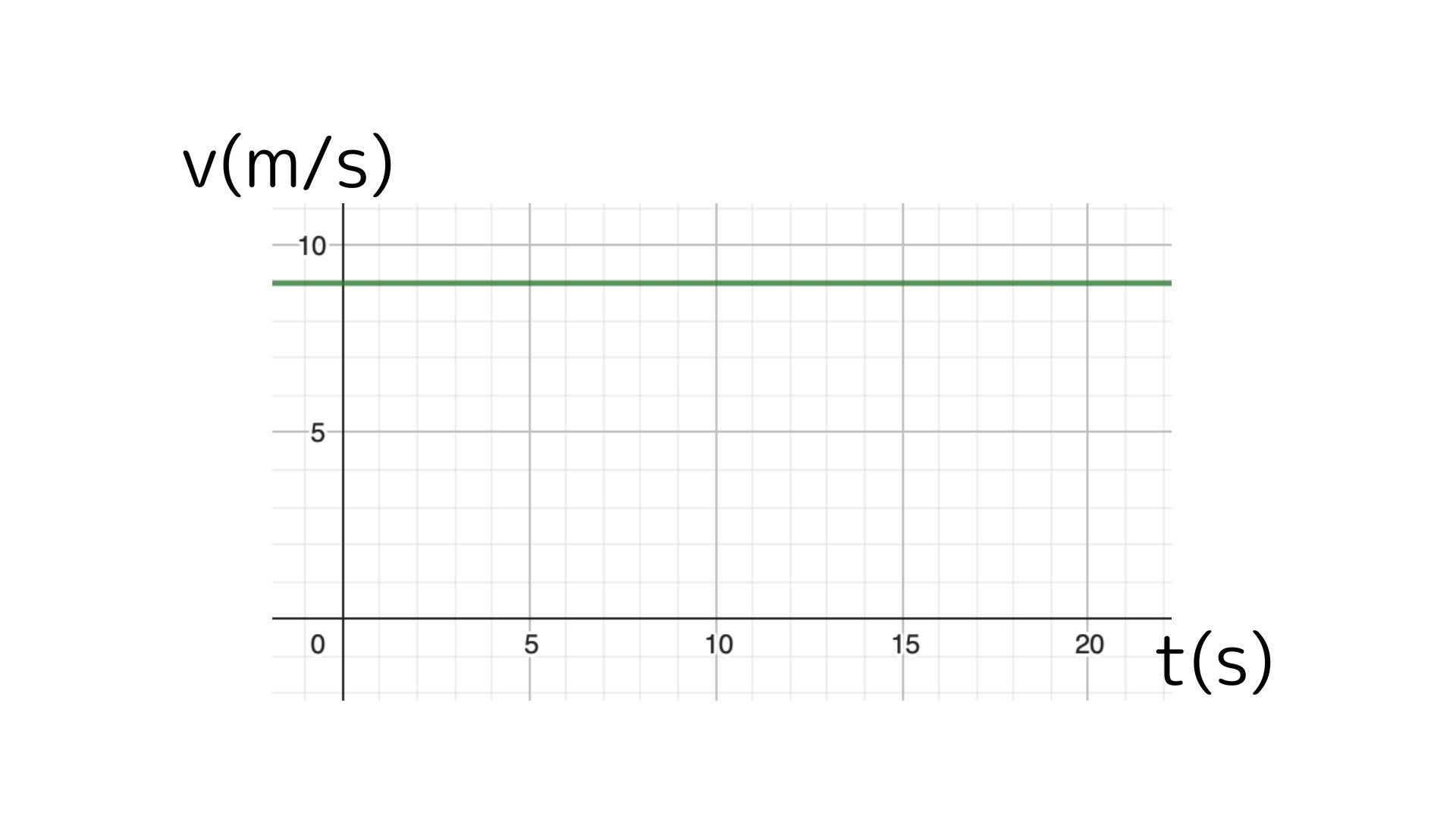
このグラフの面積を求める、つまり積分すると進んだ距離が求められます。

例えば開始してからx秒経ったときの進んだ距離は不定積分の形を使ってこのように表されます。

\begin{aligned} \int f(x)dx=F(x)+C \end{aligned}

ではこの式において$C$はどういう意味なのでしょうか？

速さは単位時間当たりの変化量で、例えば1秒当たりどれくらいの距離を進むかという値ですが、開始時間の時点でどれくらい進んでいるかわからないというのが積分定数$C$の示す意味です。

積分4

例えば東京から大阪に向かっている際に、このグラフの0秒の時点が出発点なら$C$は0となりますが、実はすでに名古屋まで進んでいる時だったりすると$C$の値は0にはなりません。この場合、$C$は350kmくらいになるでしょう。

つまり速さ（変化量）の情報だけではスタート時点ですでにどれだけ進んでいるかわからないという変数を示すのが不定積分で、そのため積分定数があるのです。

しかし定積分の場合はどうでしょうか。時間がaからbまでに進む距離と言うのは最初に進んでいた距離は関係なくなります。

積分5

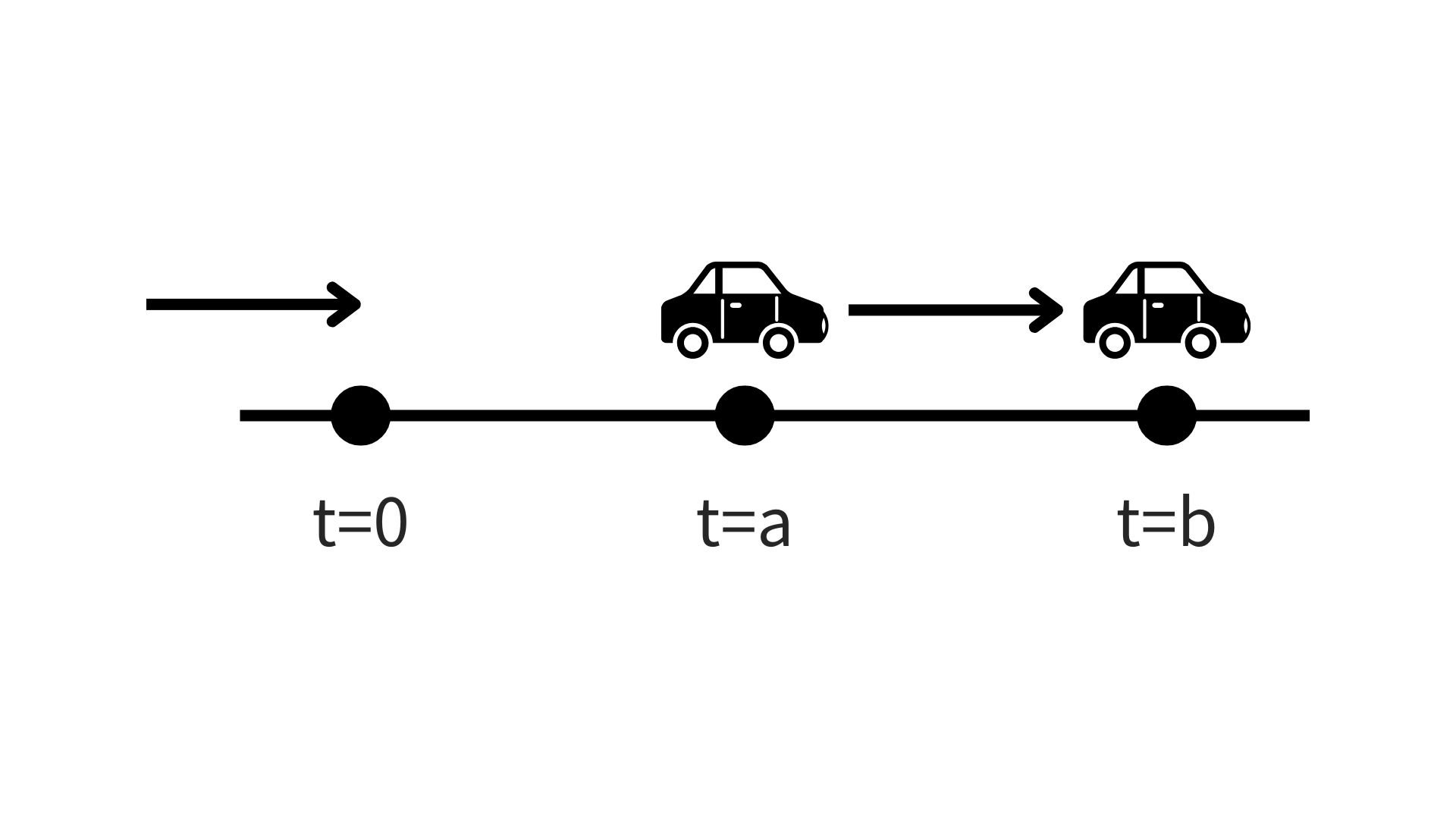
このように$t=0$の時点での不明な定数が相殺されるため、定積分には積分定数が出てこないのです。このようにもイメージされ、式としてはこのような形でも示されます。

積分6

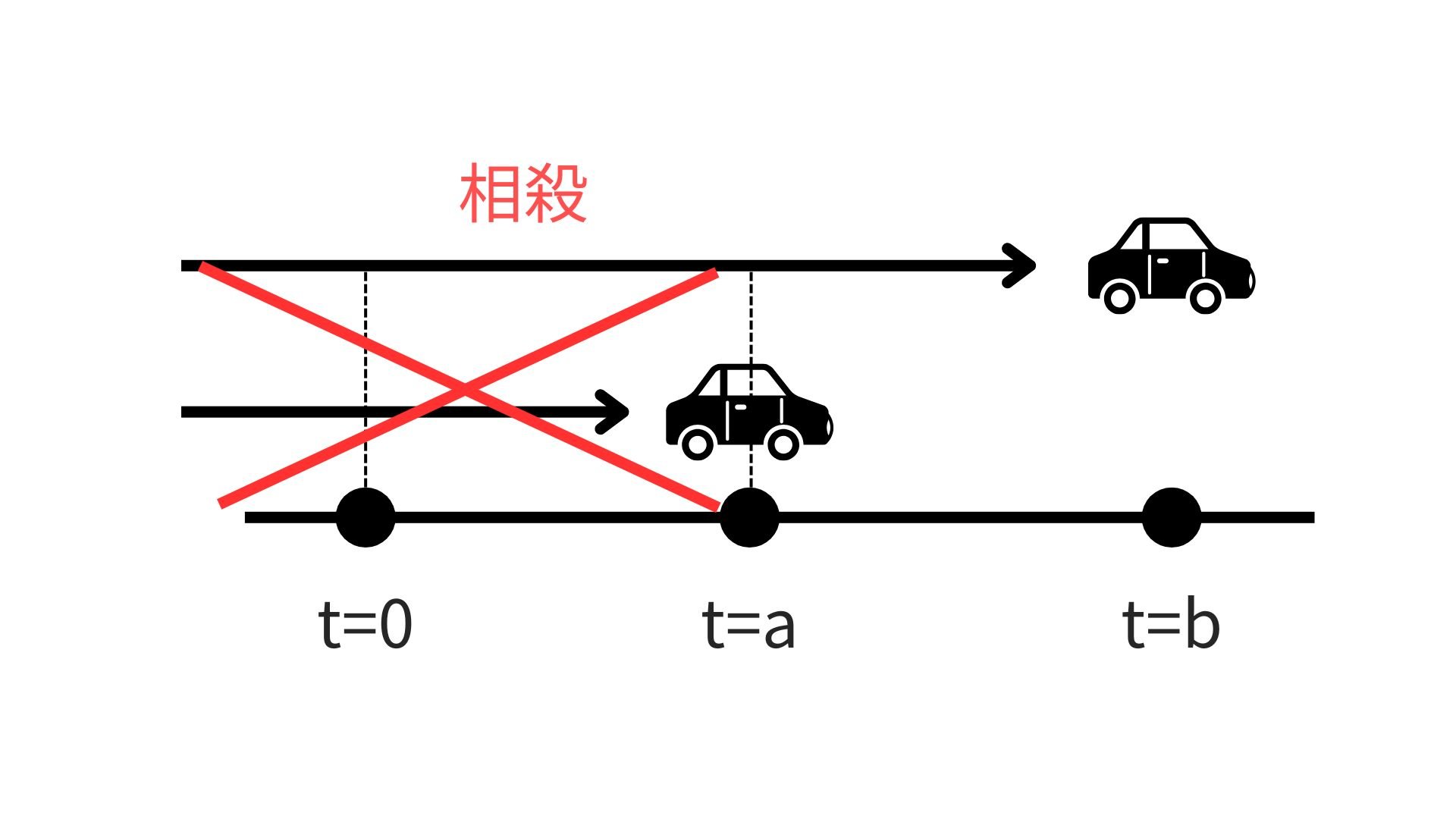
\begin{aligned} \int^b_a f(x) &= F(b)+C-\{F(a)+C\} \\ &=[F(x)]^b_a\\ &=F(b)-F(a) \end{aligned}

積分公式

ここからは積分の公式について不定積分で紹介します。定積分でも形は一緒なので、積分した形を求めてから代入して計算するようにしてください。

積分の線形性

・定数は外に出せる
$\int kf(x)dx = k\int f(x)dx$

・和の積分は分解できる
$\int \{f(x)+g(x)\}dx = \int f(x)dx+\int g(x)dx$

・差も同様に分解できる
$\int \{f(x)-g(x)\}dx = \int f(x)dx-\int g(x)dx$

数Ⅱの範囲の積分公式

$\int x^n dx= \frac{x^{n+1}}{n+1}+C $ (nは0以上の整数$)

数学Ⅲの範囲の積分公式

$\int x^a dx= \frac{x^{a+1}}{a+1}+C $ (ただし$a≠-1の実数$)

三角関数の積分

$\int \sin xdx=-\cos x+C$

$\int \cos xdx=\sin x+C$

$\int \tan xdx=-\log |\cos x|+C$

$\int \frac{1}{\cos^2x}dx=\tan x+C$

$\int \frac{1}{\sin ^2x}dx=-\frac{1}{\tan x} +C$

指数・対数の積分

$\int \frac{1}{x}dx=\log |x|+C$

$\int \log xdx=x\log x - x+C$

$\int e^xdx=e^x+C$

$\int a^xdx=\frac{a^x}{\log a}+C$

いずれも右辺を積の微分や商の微分などを使って証明することができます。

積分の応用公式

積分には数IIIの範囲にはなりますが、いくつかの応用的な公式があります。これらはいずれも覚えておく必要があるため覚えておきましょう。

置換積分(数Ⅲの範囲)

$x=g(t)$と置換すると

$\int f(x)dx=\int f(g(t))\frac{dx}{dt}dt$

厳密に言うと正しくはないのですが、覚え方として以下のように考えます。

$t$の関数を$x$で積分することはできないため、$g(t)$で置換した関数を$t$で積分する形にするが、帳尻を合わせるために$\frac{dx}{dt}$をかけると覚えておきます。

実際にこの右辺を$dt$で約分のように打ち消すと$x$で積分する形になります。

部分積分(数Ⅲの範囲)

$\int f(x)g(x)dx = f(x)G(x)-\int f'(x)G(x)dx$

部分積分についてはこちらの記事で詳しくまとめています。合わせて参考にしてみてください。
部分積分は〇〇を理解すれば簡単！なぜ必要なのか、導出も解説します

練習問題

1.次の関数の不定積分を求めよ（数Ⅱ範囲）
$f(x)=3x^2+2x+1$


解答はこちら

2.次の定積分を求めよ（数Ⅲ範囲）
$\int^2_1\frac{1}{x^2}dx$


解答はこちら

3.次の関数の不定積分を求めよ（数Ⅲ範囲）
$f(x)=\sin x-\cos x$


解答はこちら

4.次の定積分を求めよ（数Ⅲ範囲）
$\int^3_1e^xdx$


解答はこちら

まとめ

いかがでしたでしょうか。積分の定義から微分との関係、公式、使い方を数IIIの範囲まで含めて紹介しました。

積分を苦手に感じる方も多いと思いますが、微分と同じく積分は高校数学で避けては通れない重要な単元の一つです。積分は関数の任意の範囲における面積を求めることができます。

この記事を読んだ方が積分の本質を理解し、積分の解き方をマスターできるようになる手助けとなれば幸いです。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

この記事を家族や友人に教える

関連タグ

#中学生 #数学 #高校生

あわせて読みたい記事

タグ一覧

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

悩める親子の強い味方
明光プラスとは？

個別指導のパイオニアである明光義塾が集めた、学習や受験、お子さまとのコミュニケーションに役立つ情報をお届けしています。

TOPへ

学年別

おすすめ記事

Home > 明光プラス > 学習 > 積分とは○○です！積分を最初からやさしく解説し、覚えるべき公式を紹介！