2024.12.24

確率の計算式や計算方法を1から解説！簡単な計算の仕方のコツも紹介

確率の計算、というと苦手に感じる人も多いのではないでしょうか。中学や高校で扱う確率の計算方法の中には足す場合とかける場合があって混乱しやすく、公式や専門用語も多く理解が難しいと感じる人も多いでしょう。

そこでこの記事では確率の計算式や計算方法、簡単な計算の仕方を1から丁寧に、練習問題も交えて解説します。

確率を知るためには割合の理解が必要です。割合に関してはこちらの記事で詳しく解説していますので、割合を理解していない場合はこちらの記事を先に読むことをおすすめします。
パーセントの計算の仕方は？割合や歩合と合わせて1からわかりやすく解説！

そもそも確率とは？

確率は簡単に言うと「ある事象が発生する割合」です。
割合は「全体に対するある数量の比」、つまり「すべての事象に対するある事象の場合の数の比」なので、確率は以下のように定義できます。

ここで重要なのは「どの場合においても発生しやすさが平等」のときにこの式が成り立ちます。これを「同様に確からしい」と表現します。

同様に確からしいものの例としてよく使われる例はこのようなものがあります。

・10円玉を投げて表が出るか裏が出るか

一般的に10円玉を投げて表が出るか裏が出るかは同様に発生しやすいと考えられています。
そのため「表が出る」という確率は以下のように計算できます。

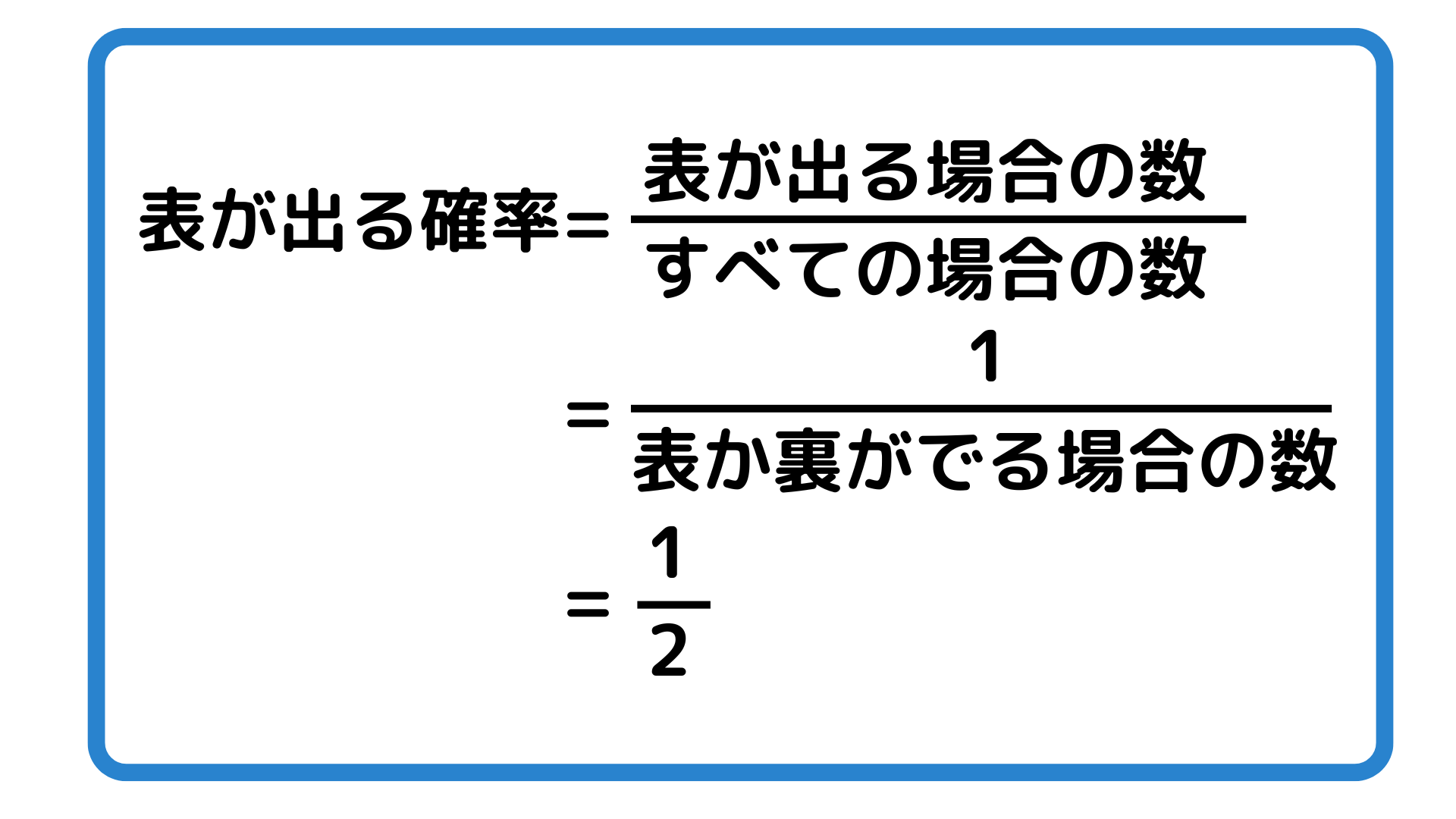
・さいころを投げて1,2,3,4,5,6のどの目が出るか

さいころも一般的にどの目が出るかは同様に発生しやすいと考えられています。
そのため「偶数が出る」という確率は以下のように計算できます。

反対に「今年の7月1日に東京都で雪が降るかどうか」のようなことは雪が降らない場合が圧倒的に多く、発生しやすさは平等ではないので「同様に確からしくない」と言えます。

場合の数を使った確率の計算の仕方

10円玉を1回投げたり、さいころを1回投げるだけの確率の計算だけなら簡単ですが、それが複数ある場合の計算をしてみましょう。

10円玉を2つ投げたときに2枚とも同じ面が出る確率について考えてみます。

同じ面が出る場合の数は「表-表」「裏-裏」の2通りで、すべての場合の数は「表-表」「表-裏」「裏-表」「裏-裏」の4通りです。

となります。このように複数ある場合においても、求める事象とすべての場合の数を洗い出すことで確率を求めることができます。

また、この場合の確率は次のように考えることもできます。

「同じ面が出る」= 「1枚目はどちらでもよいから2枚目が同じ面が出る」

1枚目にどちらかの面が出たとき、2枚目に同じ面が出る場合は1/2です。なので同じ面が出る確率は1/2と求められ、場合の数をすべて洗い出したのと同じ計算結果になりました。

このように求める方法を積の法則と言います。

積の法則を使った確率の計算の仕方

積の法則を使った確率の計算の仕方を紹介します。事象A, Bが独立のとき、Aが起きてさらにBが起きる確率は「Aが起きる確率×Bが起きる確率」と求められます。

事象A,Bが独立である、というのは事象A,Bがお互いに影響しない状態を言います。
例えば、2枚の10円玉を投げたときに1枚目が表だろうと裏だろうと2枚目の出る面に影響は与えません。
このように片方の事象がもう片方の事象が起こる確率に影響しない場合、それらの事象は独立である、と言います。

積の法則を使い、先ほどの確率の計算を紐解くと、1枚目に表か裏が出る確率は1のため

同じ面が出る確率 = 1枚目に表か裏が出る確率 × 2枚目に同じ目が出る確率となります。よって、

と積の法則で確率を求めていることになります。

事象A, Bが独立のとき、Aが起きてさらにBが起きる確率は「Aが起きる確率×Bが起きる確率」と表されるのが積の法則です。事象がそれぞれ独立の場合、この積の法則が成り立ちます。

事象が従属の場合の確率の計算の仕方

事象が独立でないときを従属と言います。例えばくじ引きで3本の中に当たりが1本入っていて2本引く場合の
・1本目で当たる
・くじを戻さず引いて2本目で当たる
これらの事象は従属と言えます。

1本目で当たった場合、2本目で当たる確率は0です。逆に1本目が外れだった場合、2本目で当たる確率は1/2です。

このように1本目の結果次第で2本目で当たる確率が変わってしまう状態を従属と言います。

2本引いて2本目で当たる確率は1本目で外れて2本目で当たる確率をかけて求めます。

2本目で当たる確率 = 1本目が外れの確率 × 2本目が当たりの確率　となるので、

ちなみに1本目で当たる確率も1/3で、3本目で当たる確率も1/3です。なのでくじ引きは引く順番に関わらず同じ確率で当たるため公平だと言われています。

和の法則を使った確率の計算の仕方

確率には和の法則というのもあります。
事象A,Bが排反のときAとBのどちらかが起きる確率は「Aが起きる確率＋Bが起きる確率」と求められます。

事象A,Bが排反であるというのは事象A,Bが同時に起きない状態です。
例えば10円玉を投げて表が出るという事象と裏が出るという事象は同時に起きません。
そのため表か裏が出る確率は

表か裏が出る確率=表が出る確率+裏が出る確率なので、

と和の法則で求められます。

この積の法則と和の法則はすべての場合の数や、ある事象の場合の数を数え上げることに時間がかかる場合に短時間で確率を計算するコツのため、特に大学受験で数学を使う人は必須になります。必ず理解しておきましょう。

・事象がそれぞれ排反の場合、和の法則が成り立つ

排反でないときの確率の求め方

さいころを投げて偶数か3の倍数が出る確率を求める場合、6は偶数でもあり、3の倍数でもあります。そのため和の法則を使って確率を求める場合、共通の部分、つまり6の場合を差し引く必要があります。

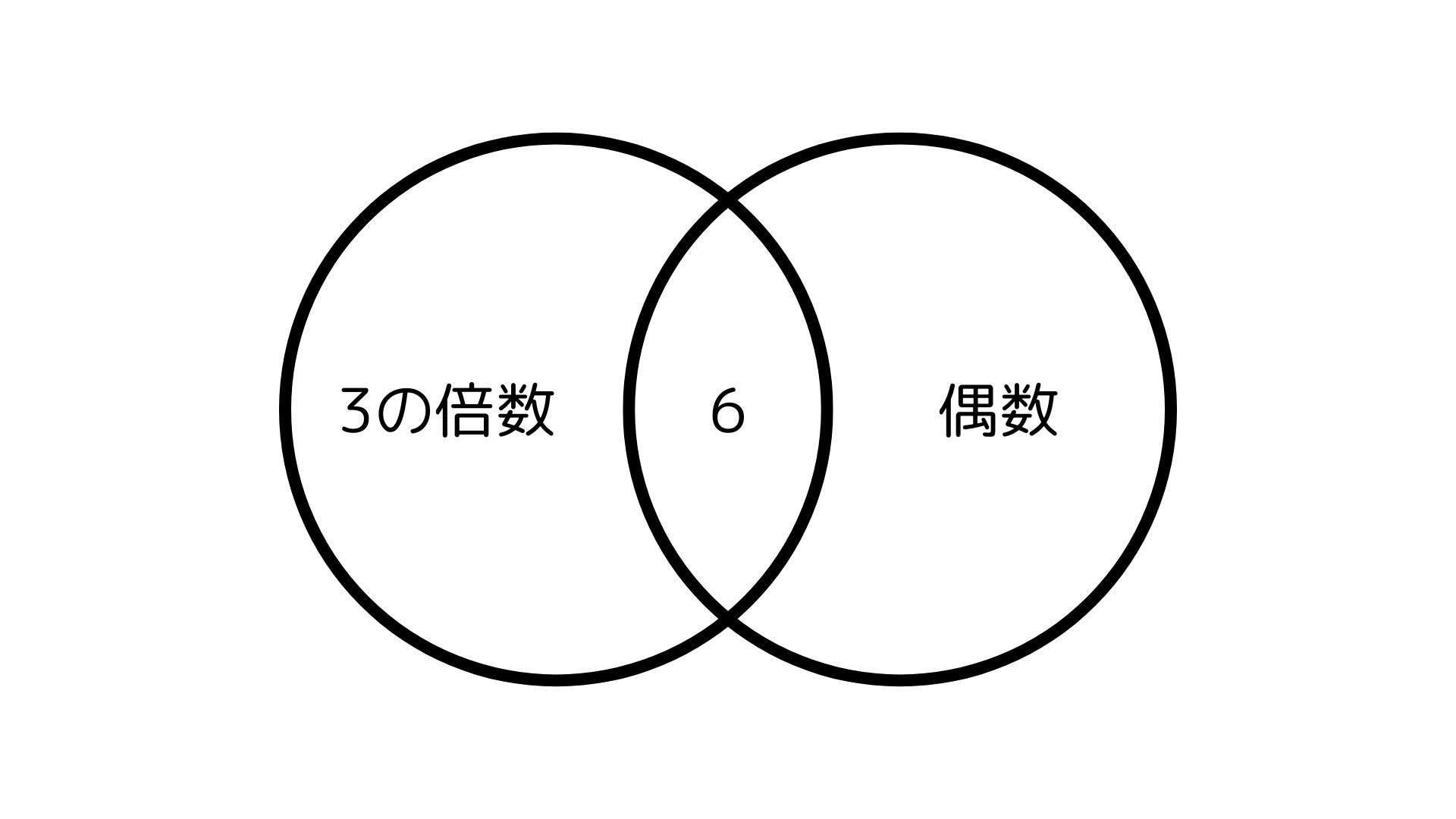
偶数か3の倍数が出る確率=偶数が出る確率+3の倍数が出る確率-6が出る確率なので

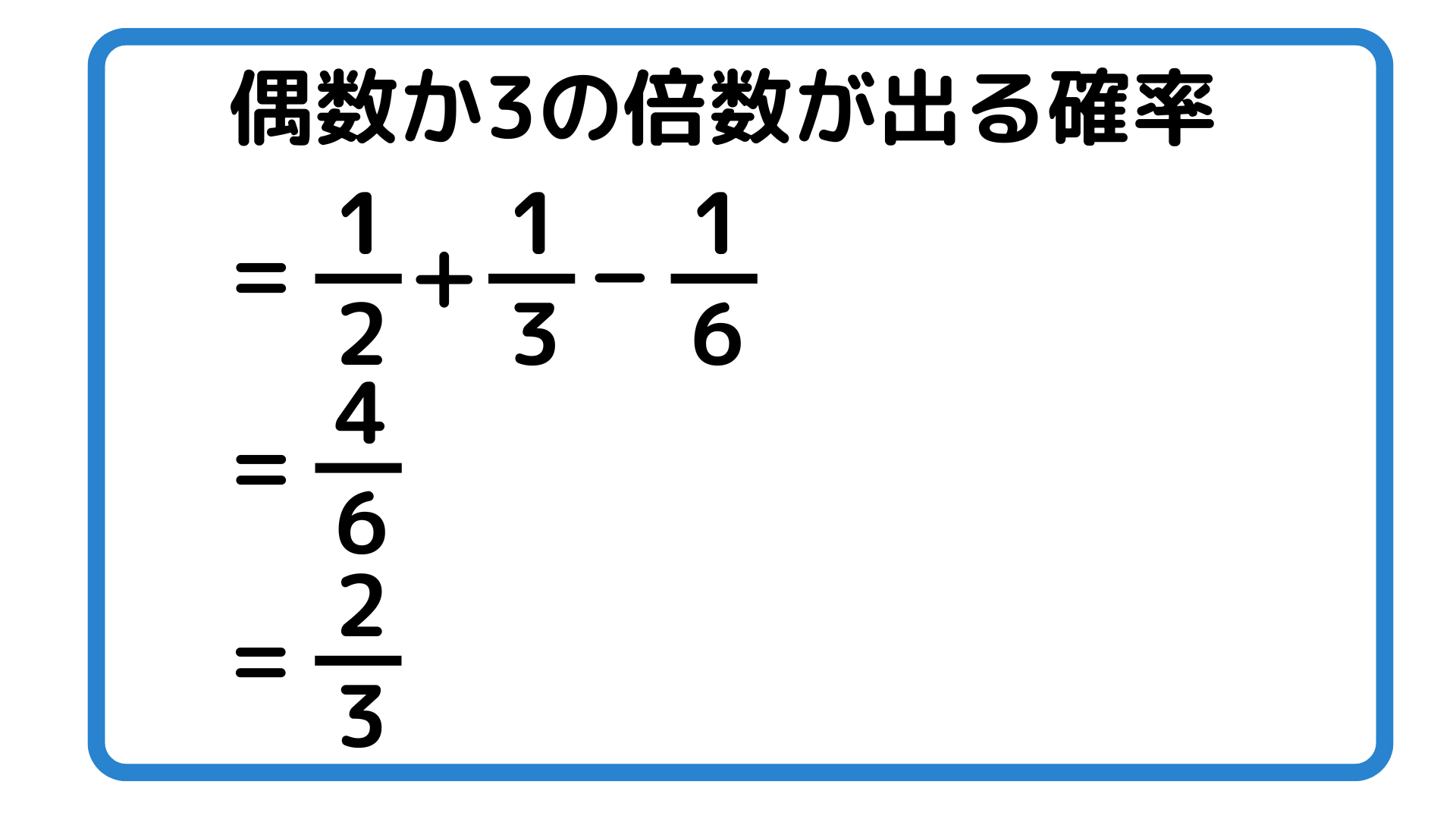
偶数か3の倍数というのは2,3,4,6のため4/6=2/3と計算結果が一致することがわかります。

余事象を使った確率の計算のコツ

さいころを3回投げて少なくとも1回は1が出る確率を求めるというように、「少なくとも1回」という確率を求める場合、余事象を使って考えると簡単です。

すべての確率から「1回も1が出ない」、つまり3回とも2~6が出るという確率を引いて求めればよいので、

3回投げて少なくとも1回1が出る確率=1-1回も1が出ない確率なので

これを素直に解こうとすると以下の場合分けが必要になり計算が大変になります。

・ 1回1が出る確率
・ 2回1が出る確率
・ 3回1が出る確率

練習問題

問.1から100まで書いたカードが1枚ずつあり、そこから1枚引いたときに偶数または5の倍数である確率を求めよ

解答はこちら

問.さいころを3回投げて出た目の掛け算が偶数になる確率を求めよ

解答はこちら

まとめ

いかがでしたでしょうか。本記事では、確率の計算式や計算方法について公式や計算のコツを交えながら解説しました。

中学生の皆さんは高校数学で扱う本格的な確率に向けて少しでも理解を進めましょう。

高校生の皆さん、特に大学受験で数学を使う皆さんは共通テストにおいて確率は避けられない道です。しっかりと復習をして理解し、短時間で解ける計算方法を確実にマスターしましょう。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

あわせて読みたい記事

模試の勉強法とは？模試の成績の上げ方・年代別の受験への活かし方を紹介

2025.07.18

模試は志望校合格のための“羅針盤”とも言える存在です。しかし、「模試って結局どう活用したらいいの？」「成績がなかなか伸びない…」と感じている方も多いのではないでしょうか。この記事では、模試...
微分とは？微分は○○です！定義・公式・使い方を解説

2025.07.07

高校数学の教育課程で避けては通れない微分。苦手に感じていたり、つまずいたりしてしまう方も多いのではないでしょうか。本記事では、微分とは何かという定義から、基本公式・実際の使い方・例題・応用までを、...
三平方の定理（ピタゴラスの定理）とは？計算の仕方と証明をやさしく解説！

2025.07.04

もくじ三平方の定理(ピタゴラスの定理)とは？三平方の定理(ピタゴラスの定理)の応...