2024.10.15

標準偏差とは？標準偏差の求め方、偏差値、分散の意味を1からわかりやすく解説！

数学Ⅰで出てくる標準偏差は、データの特徴を表す指標の1つで、多くの人が混乱しやすいものです。

特に、偏差値との違いがわからなかったり、その元になる「分散」の意味がピンとこなかったりするという方も少なくないでしょう。しかし、これらの概念は言葉の意味やイメージを理解すると、ぐっと身近なものになります。

この記事では、全く知識がない方でも理解できるように、標準偏差の意味から計算方法まで丁寧に解説していきます。

標準偏差が生まれた理由

データの特徴を表す指標として最も有名なものは「平均値」です。平均値はすべてのデータの和をデータの個数で割ったものです。平均値だけではデータの詳細な特徴を捉えきれない場合があります。

例えば、野球のピッチャーが2人いて、どちらのコントロールがよいかを競うとしましょう。それぞれがど真ん中めがけて2球を投げ、このような結果になったとします。

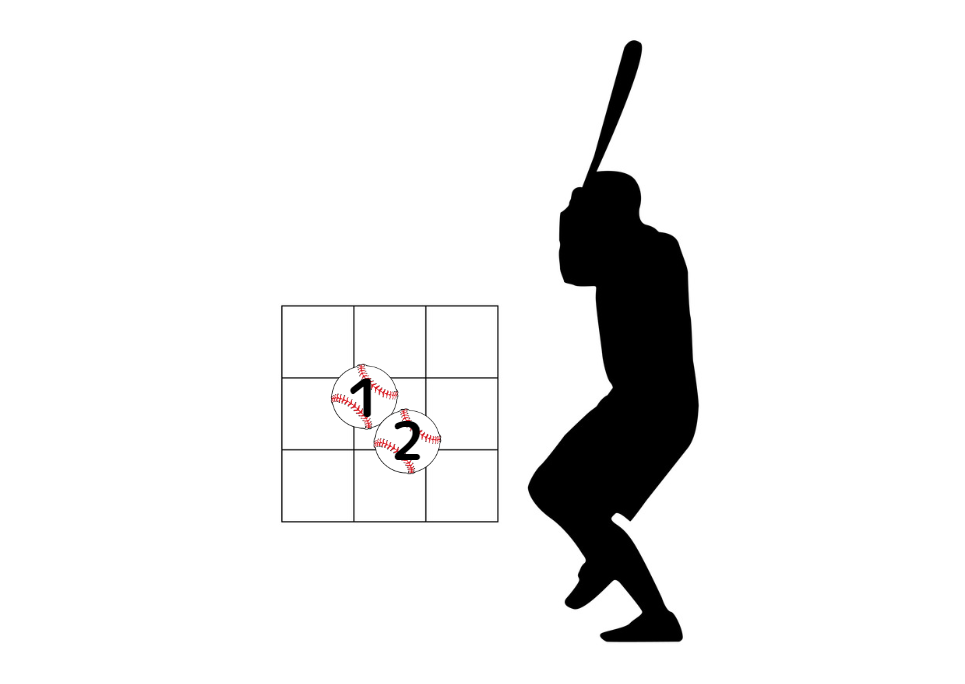
この2つの結果の平均値（中間）は、どちらもほぼど真ん中であるため、平均値だけで判断すれば、コントロール勝負は引き分けと見なされます。

しかし、ピッチャーAの球はばらつきが大きく、ピッチャーBは狙い通りの位置に集まっていることが一目でわかります。ど真ん中を狙ってこの結果になったなら、明らかにピッチャーBのほうがコントロールがよいと言えます。

この例からもわかるように、コントロールのよし悪しを判断するのに平均値だけでは不十分です。

データのばらつきを表す新たな指標「分散」

ここでコントロールのよさを考えるときに「どれだけ平均値（中心）からずれているのか」を新たな指標として考えてみましょう。ここでは話を簡単にするために、横のずれは考えず、高さのみ考えることにします。

中心を0とした時の高さのずれは以下の通りです。

	1球目	2球目
ピッチャーA	40cm	-40cm
ピッチャーB	5cm	-5cm

この平均からのずれのことを「偏差」と呼びます。

偏差はプラスとマイナスがあるため、そのまま足し合わせると結果は0になってしまいます。そこで、±の影響をなくすために偏差を2乗し、その平均を取ることにしました。これが、データがどれだけ平均（中心）からずれているか、すなわちどれだけ散らばっているかを示す「分散」です。

分散の定義を言葉と式で表すとこのようになります。

今回で言うとそれぞれの結果の分散は具体的にこのように計算されます。

ピッチャーA
$\frac{1}{2}×((40-0)^2 + (-40-0)^2) = 1600$
ピッチャーB
$\frac{1}{2}×((5-0)^2 + (-5-0)^2) = 25$

結果として、ピッチャーAの分散は1600、ピッチャーBの分散は25という結果になりました。
分散が小さいほど、データのばらつきが少ないことを意味します。

分散から派生して生まれた指標「標準偏差」とは？

分散は偏差を2乗して求めているため、元のデータとの単位が異なります。今回の野球の例で言うと偏差は$cm$ですが、分散は$cm^2$になります。

この単位の違いをなくし、元のデータと同じ単位にするために、分散の平方根(2乗する前の数のこと)を取ります。この新しい指標を標準偏差と呼び、σ（シグマ）で表します。このことから先ほどの分散は$σ^2$と表記されます。

標準偏差の定義は次の通りです。

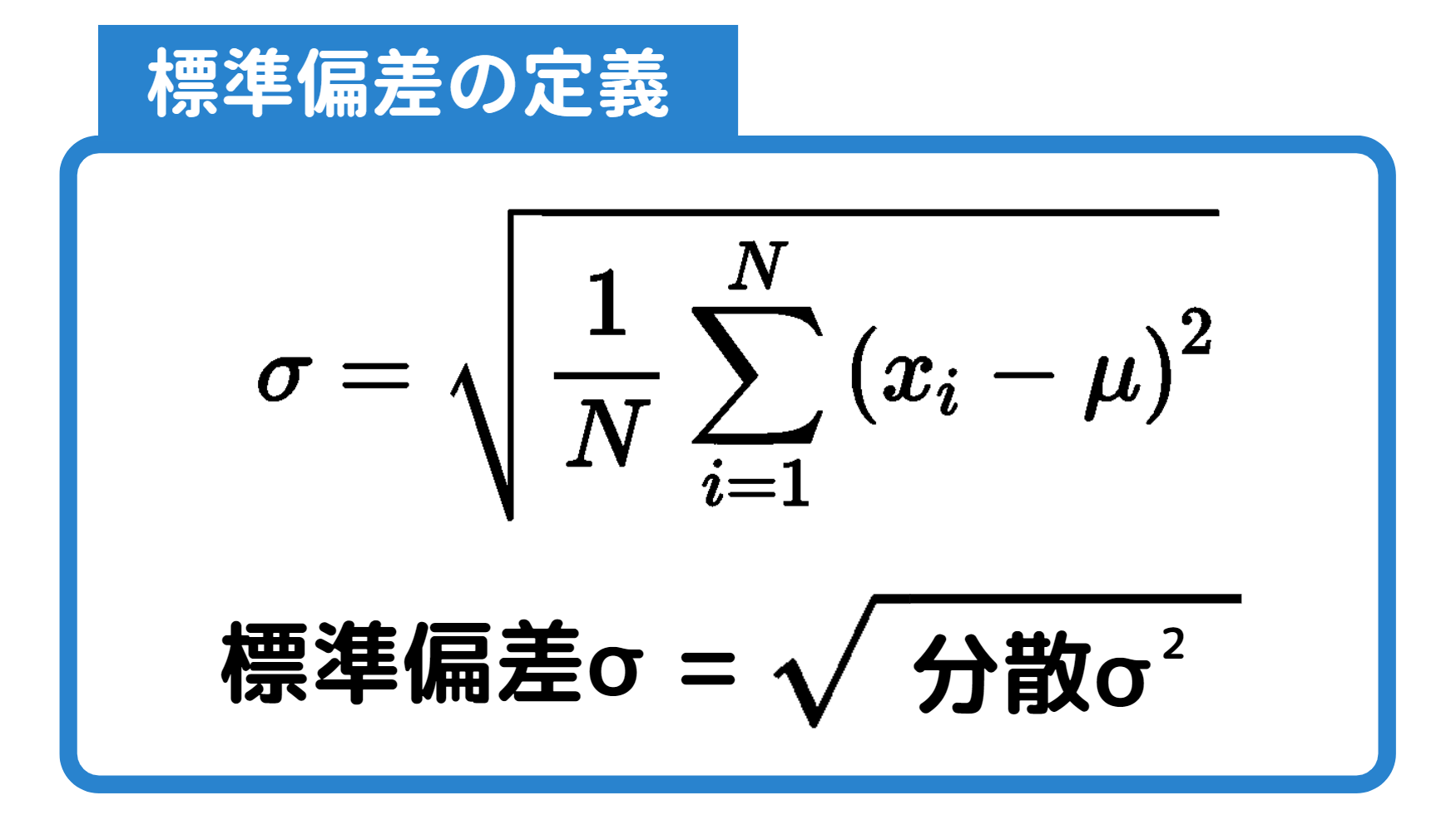
分散から標準偏差の具体的な計算は以下の通りです。

ピッチャーAの標準偏差
$\sqrt {1600}$ = 40
ピッチャーBの標準偏差
$\sqrt{25}$ = 5

このように、標準偏差も分散と同様に、値が小さいほどデータのばらつきが少ないことを示します。

「偏差値」は標準偏差と平均値から計算できる

模試や高校・大学の難易度で使われる「偏差値」は、異なるデータ集団の中で個々のデータを比較するために作られた指標です。例えば、以下のようなテスト結果があったとしましょう。

	国語	算数
自分	70点	55点
A君	80点	50点
B君	90点	45点

簡単に考えるために、母集団は自分とA君とB君の3人とします。

自分のテスト結果は国語が70点、算数が55点ですが、どちらのほうがよくできたと言えるでしょうか？単純に点数だけを見ると、国語のほうが算数より15点高いです。しかし、平均点と比較すると国語は平均点より低く、算数は平均点よりも高いことがわかります。

このような場合に、自分のテスト結果をほかと比較するために変換した指標が「偏差値」です。偏差値は、平均を50にするように計算される指標であり、その計算式は以下の通りです。

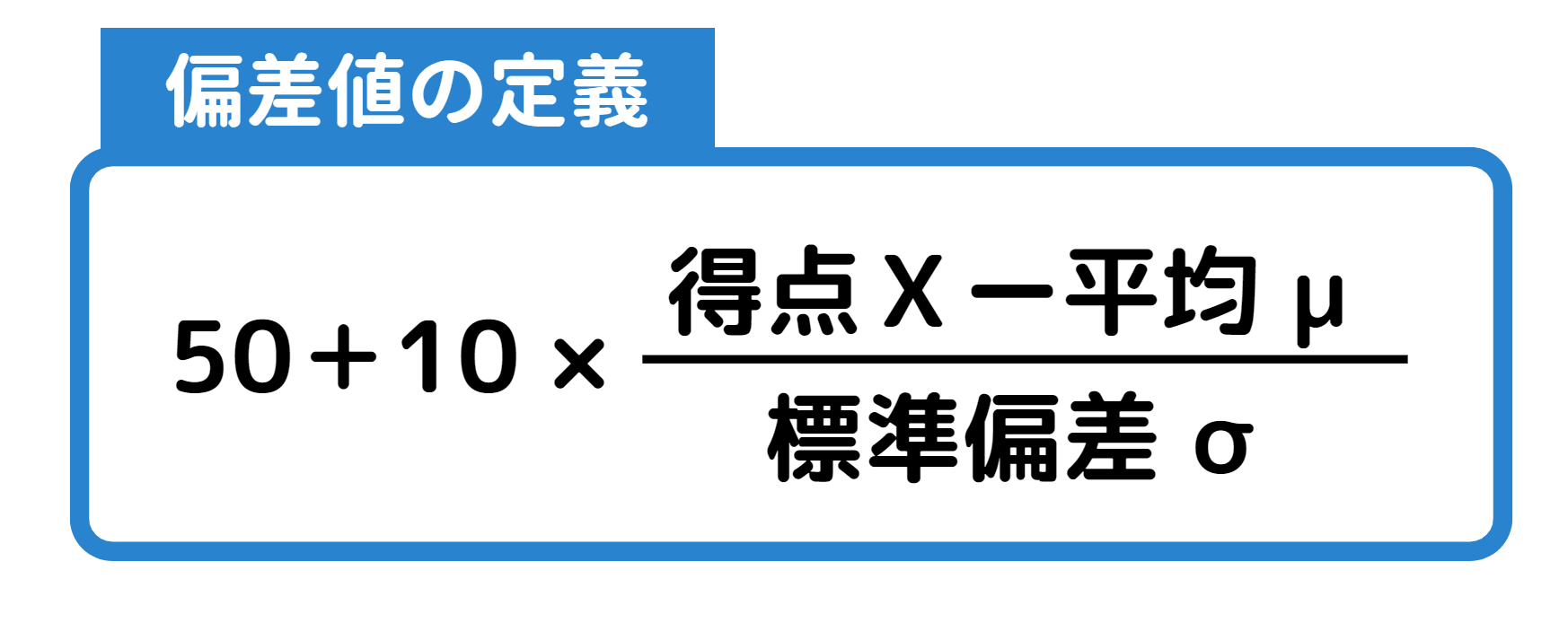
この式からわかるように、得点が平均点と同じ場合、右側の項が0になり、偏差値は50になります。それでは、具体的に国語と算数の偏差値を求めていきましょう。

国語の偏差値

国語の平均点は80点で、標準偏差は次のように計算されます。

σ国語
= $\sqrt{\frac{1}{3} × ((70-80)^2 + (80-80)^2 + (90-80)^2)}$
= $\sqrt{\frac{200}{3} }$
≒ $\sqrt{66.7 }$
≒ 8.17

よって自分の国語の偏差値は
$50 + 10 × \frac{70 - 80}{8.17}$
≒ 37.8
と求まります。

算数の偏差値

算数の平均点は50点のため、標準偏差はこのように計算されます。

σ算数
= $\sqrt{\frac{1}{3} × ((55-50)^2 + (50-50)^2 + (45-50)^2)}$
= $\sqrt{\frac{50}{3} }$
≒$\sqrt{16.7 }$
≒ 4.09

よって自分の算数の偏差値は
$50 + 10 × \frac{55 - 50}{4.09}$
≒62.2
と求まります。

結果として、国語の偏差値は37.8で平均の50より低く、算数の偏差値は62.2で平均より高いことがわかります。このように偏差値という指標を使うことで、異なる集団の中で自分の点数がどれくらいの位置にいるかを、明確に示すことができます。

ただし、偏差値は母集団の質やデータの量に依存するため、信頼性には注意が必要です。偏差値の詳細については、こちらの記事で詳しく解説していますので、合わせて参考にしてください。
偏差値の調べ方とは？計算方法から偏差値アップのコツまで解説

まとめ

いかがでしたでしょうか。本記事では、標準偏差の意味と計算方法について解説しました。

標準偏差の計算は少し複雑に感じるかもしれませんが、計算方法や使い方を理解しておくことは非常に重要です。

今回紹介した計算方法がスムーズに出てくるように、標準偏差に関する演習問題を繰り返し解きましょう。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

あわせて読みたい記事

微分とは？微分は○○です！定義・公式・使い方を解説

2025.07.07

高校数学の教育課程で避けては通れない微分。苦手に感じていたり、つまずいたりしてしまう方も多いのではないでしょうか。本記事では、微分とは何かという定義から、基本公式・実際の使い方・例題・応用までを、...
三角関数（sin, cos, tan）入門！公式をわかりやすく覚える方法を紹介！

2025.06.26

三角関数では$\sin$(サイン),$\cos$(コサイン),$\tan$(タンジェント)や$\theta$(シータ)といった聞きなれない呪文のような言葉が多く出てくるのに加え、覚える公式が多いため...
三角比(sin, cos, tan)とは？覚え方と三角比の表も紹介！

2025.06.20

三角比ではsin(サイン),cos(コサイン),tan(タンジェント)やθ(シータ)といった聞きなれない呪文のような言葉がでてくるうえに、覚えることも多いため苦手意識を持っている方も多いのではないで...