2025.06.26

三角関数（sin, cos, tan）入門！公式をわかりやすく覚える方法を紹介！

三角関数では$\sin$(サイン),$\cos$(コサイン),$\tan$(タンジェント)や$\theta$(シータ)といった聞きなれない呪文のような言葉が多く出てくるのに加え、覚える公式が多いため、苦手だというお子さまも多いのではないでしょうか。

しかし、三角関数はほかの単元でも出てくる重要な単元ですので、苦手なままにしておくことは定期テストや受験に悪影響を及ぼします。

そこでこの記事では、三角関数とは何か、三角関数の公式を1からわかりやすく解説します。

三角関数を理解するのに必須な三角比についてはこちらの記事で詳しく紹介しています。
三角比とはなにか、$\sin$(サイン)・$\cos$(コサイン)・ $\tan$(タンジェント)の基礎がわからない方、三角比の表の使い方がわからない方はまず、こちらの記事から見て基礎を深めましょう。
三角比(sin, cos, tan)入門！表の使い方とわかりやすい公式の覚え方を紹介！

三角関数とは？三角比の拡張~単位円による定義~

三角比では直角三角形を用いて$\sin$(サイン),$\cos$(コサイン),$\tan$(タンジェント)の解説をしました。

しかし、高校の数学で習う三角比には基準とする角度が90度以上のものがでてきます。

三角形の内角の和は180度であるため、直角三角形以外で考える必要があり、生み出されたものが単位円による定義です。

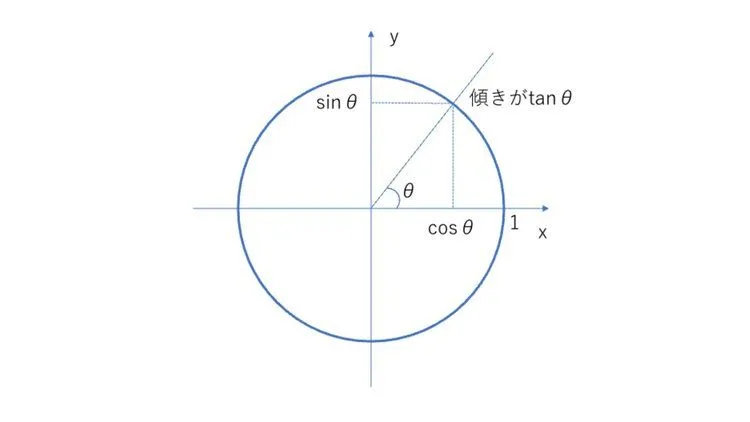
半径1の円を$xy$平面で考えると、原点から$\theta$の角度で半直線を引いたときに、半直線と円の交点ができます。その交点の$y$が$\sin \theta$、$x$が$\cos \theta$、傾きが$\tan \theta$とするという定義です。

$\theta$が90度までの場合は直角三角形の定義と同じになりますが、この拡張された単位円の定義を用いれば、任意の実数$\theta$(シータ)で$\sin$(サイン),$\cos$(コサイン),$\tan$(タンジェント)を定義できます。

この$\theta$を用いた式のことを三角関数と呼びます。

三角比の相互関係と周期性に関する公式は導出可能になろう！

三角比には暗記してすぐに引き出せるようにするべき公式がいくつかあります。三角比の相互関係と呼ばれるものや、周期性に関する公式です。

※$\theta$(シータ)は未知の角度としてよく使われている記号です。

これから紹介する式をすべて暗記しようとするのは並大抵のことではありません。すべての公式が単位円やピタゴラスの定理で導出することができるので、すべてを暗記するのではなく、素早く確認できるように訓練しましょう。

相互関係の式

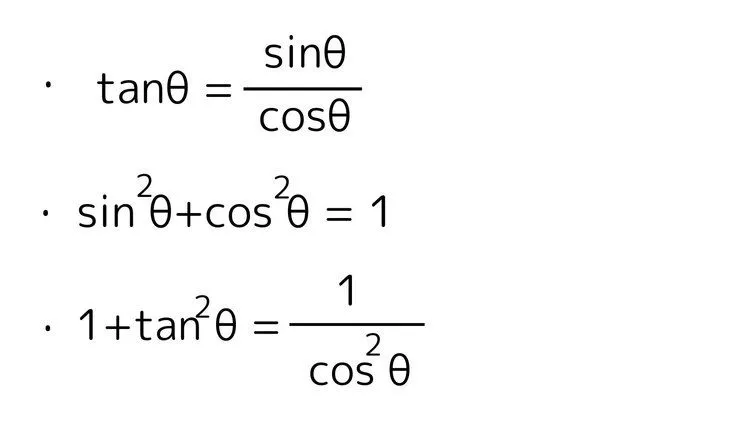
単位円の定義から傾きが$\tan \theta$なので、$\sin \theta$が$y$、$\cos \theta$が$x$だと理解していれば、$\tan \theta$はこのように表せます。

ほかの2つの式は単位円とピタゴラスの定理を用いれば導出することができます。

真ん中の式は単位円とピタゴラスの定理そのままです。下の式は真ん中の式全体を$\cos^2 \theta$で割り、$\dfrac{\sin^2 \theta}{\cos^2 \theta} = \tan^2 \theta$を代入することで導出できます。

三角比の対称性

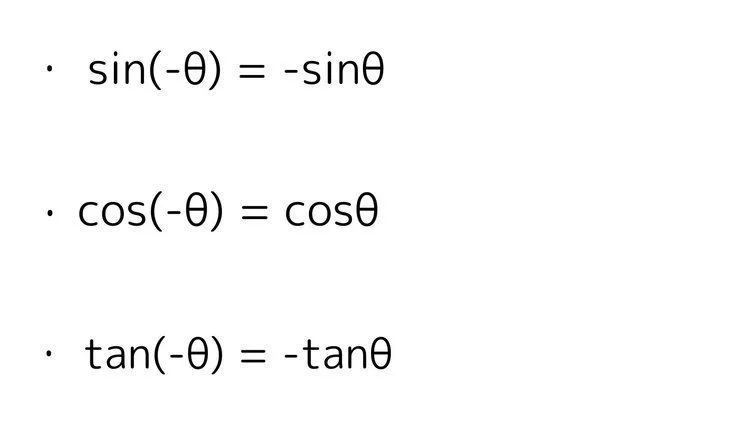
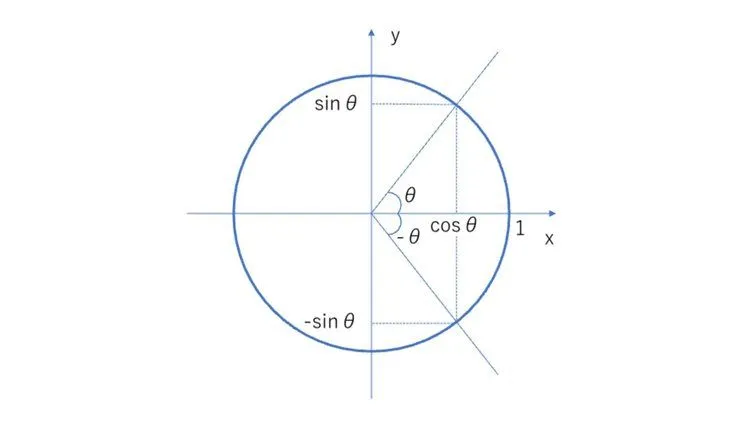
こちらは単位円で考えるとわかりやすいです。

$\theta$が負になると反対の時計回りに角度を取り、半直線を引きます。その際に、$y$($\sin \theta$)と傾き($\tan \theta$)の正負は反転しますが、$x$($\cos \theta$)の正負は反転しません。

$\dfrac{\pi}{2} - \theta$の三角比

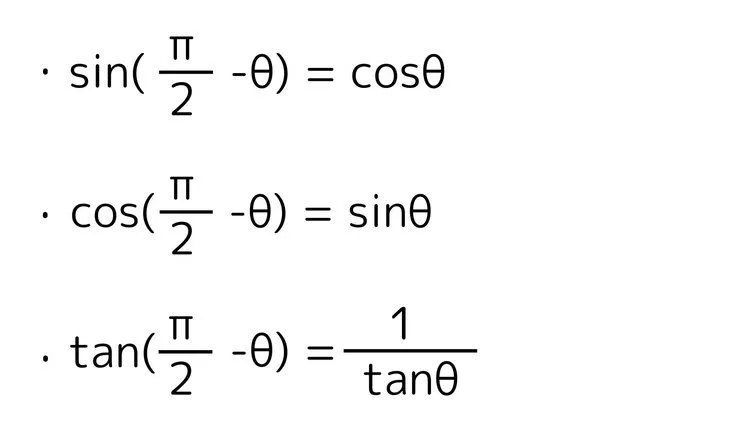
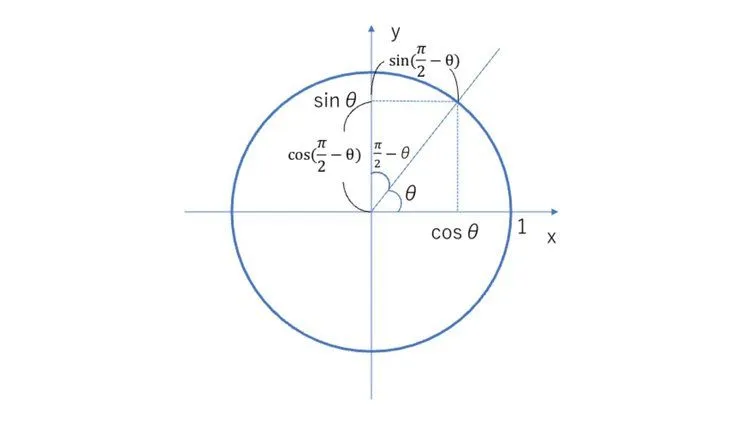
こちらも単位円と直角三角形で考えるとわかりやすいです。
$\dfrac{\pi}{2}$(直角)から$\theta$を引いた角度でできる直角三角形に着目すると、三角比はの下の図のように表せます。同じ長さの部分を比べると上記のようになることがわかります。また、傾きである$\tan$も逆数となることがわかります。

三角比の平行移動

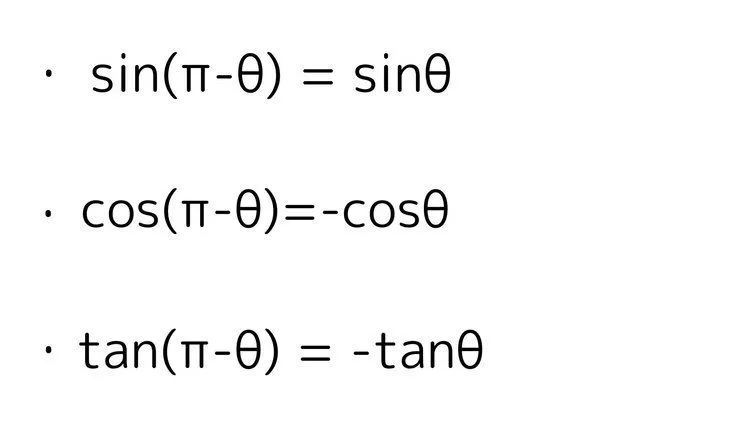
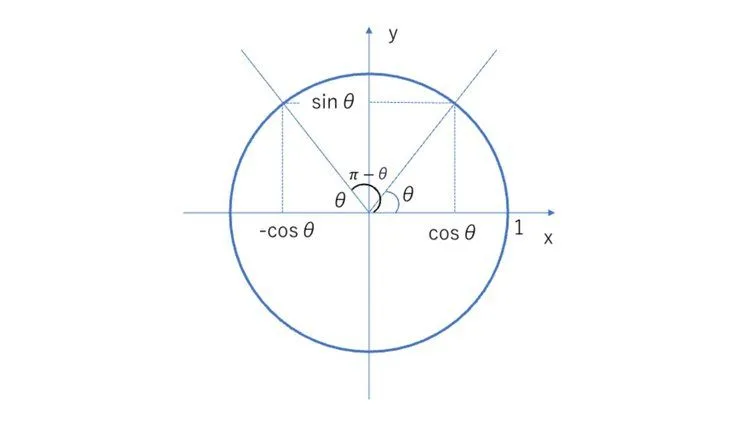
こちらも単位円で考えるとわかりやすいです。

$\pi - \theta$の反直線を引くと$x$($\cos \theta$)と傾き($\tan \theta$)の正負は反転しますが、$y$($\sin \theta$)の正負は反転しません。

このほかにも$2\pi$や$3\pi$、$\dfrac{5}{2}\pi$を足したり引いたりなどキリがありませんので公式の紹介はここまでにしますが、同様の考え方を用いれば紹介した公式と合わせて導出することができます。

素早く確認できるようになるまで問題演習をしましょう。

三角関数の完全暗記公式

最後に三角関数の難関、加法定理とそこから導出できる積和の公式について紹介します。

こちらも図形を書くことで導出できますが、時間がかかるのに加え、導出に慣れていない場合はミスが多くなるため必ず暗記するようにしましょう。

加法定理

①に関しては咲いたコスモスコスモス咲いたと覚えましょう。

①を暗記しておくと②は$\beta$を$-\beta$にして、正負が変わるのは$\sin$だけなので導出できます。

③はコスモスコスモス咲いた咲いたと覚えておきましょう。

③を暗記しておくと④もβを-βにして正負が変わるのはsinだけなので導出可能です。

⑤,⑥は①と③、または②と④と$\tan \alpha = \dfrac{\sin \alpha}{\cos \alpha}$から導出可能ですが、⑤に関しては語呂合わせで「イチマイタンタン、タンプラタン」とリズムよく覚えましょう。イ(チ)マイ(ナス)タン(ジェント$\alpha$)・タン(ジェント$\beta$分の)、タン(ジェント$\alpha$)プラ(ス)タン(ジェント$\beta$)の略です。

⑥は⑤の$\beta$を$-\beta$にすると$\tan(-\beta)=-\tan \beta$から導出可能です。

2倍角の公式

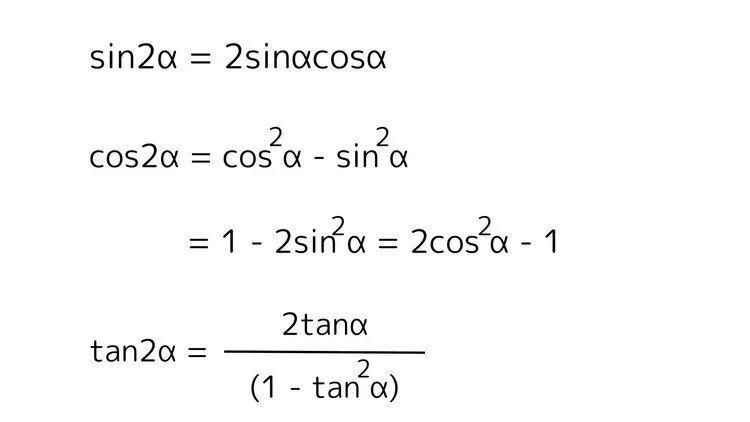
これらの公式は加法定理の$\beta$を$\alpha$に変換するだけで簡単に導出できます。

3倍角の公式

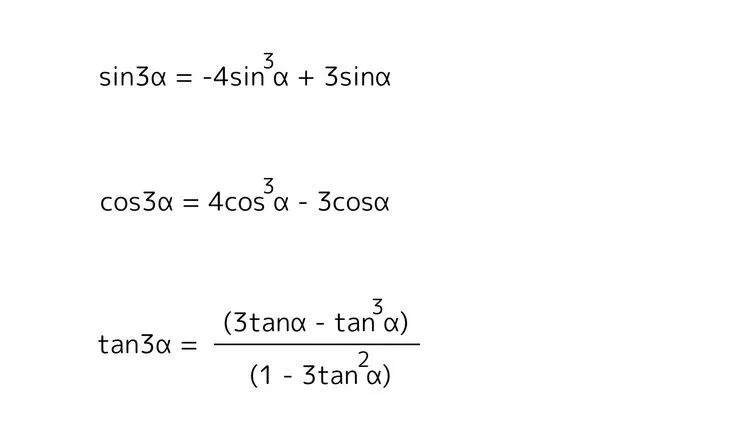
これらの公式も加法定理で導出できますが、手間がかかるのに加えて計算ミスをしやすいので暗記するのが無難です。

半角の公式

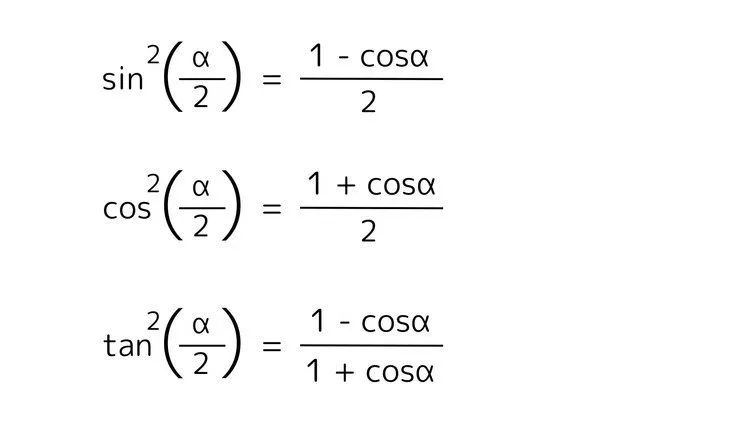
これらの公式は以下の2倍角の公式

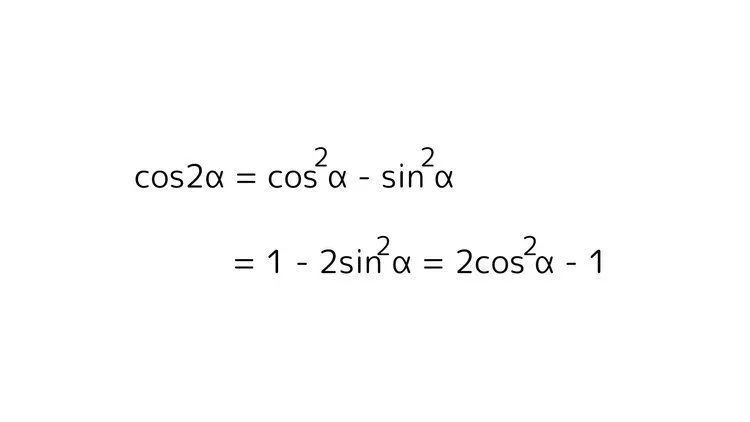
の$\alpha$に$\dfrac{\alpha}{2}$を代入することで導出可能です。

$\tan$の半角の公式は$\sin$と$\cos$の半角の公式から導出しましょう。

積和の公式

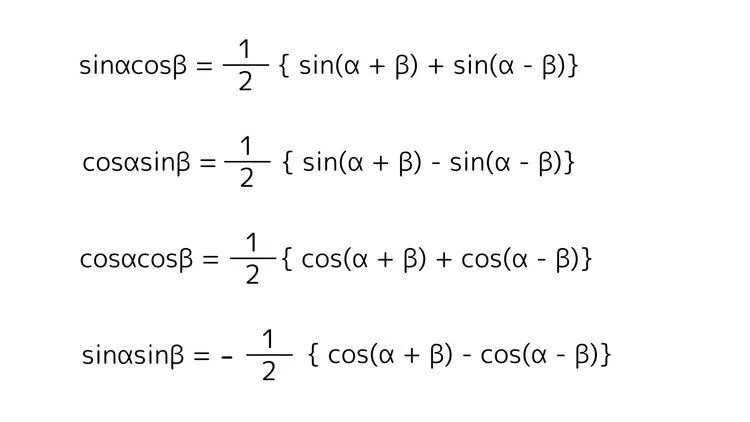
これらの公式は加法定理を用いることで導出可能です。

和積の公式

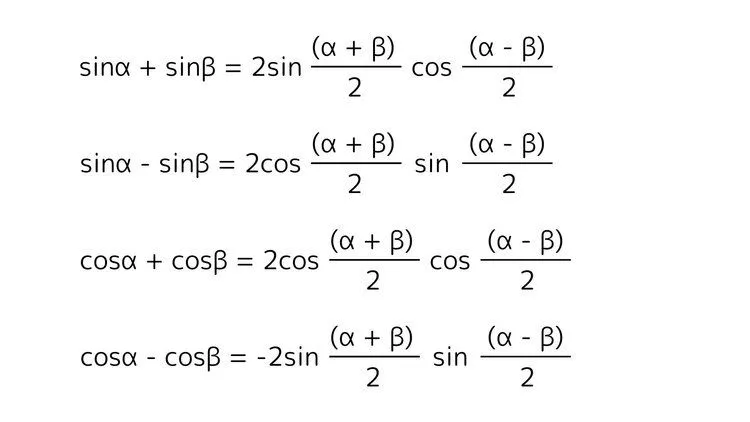
これらの公式は少しトリッキーですが

$\alpha = \dfrac{\alpha + \beta}{2},\beta = \dfrac{\alpha - \beta}{2}$

として左辺に代入し、加法定理で展開することで導出することができます。

三角関数の合成の公式

三角関数の合成とは2つの三角関数を1つの三角関数にまとめる方法のことをいいます。

複数の三角関数の場合、定義域はわかりづらいですが、まとめることで定義域がわかるようになるため、最大値・最小値が簡単に求められるようになります。

それでは実際に複数の関数をまとめてみましょう。

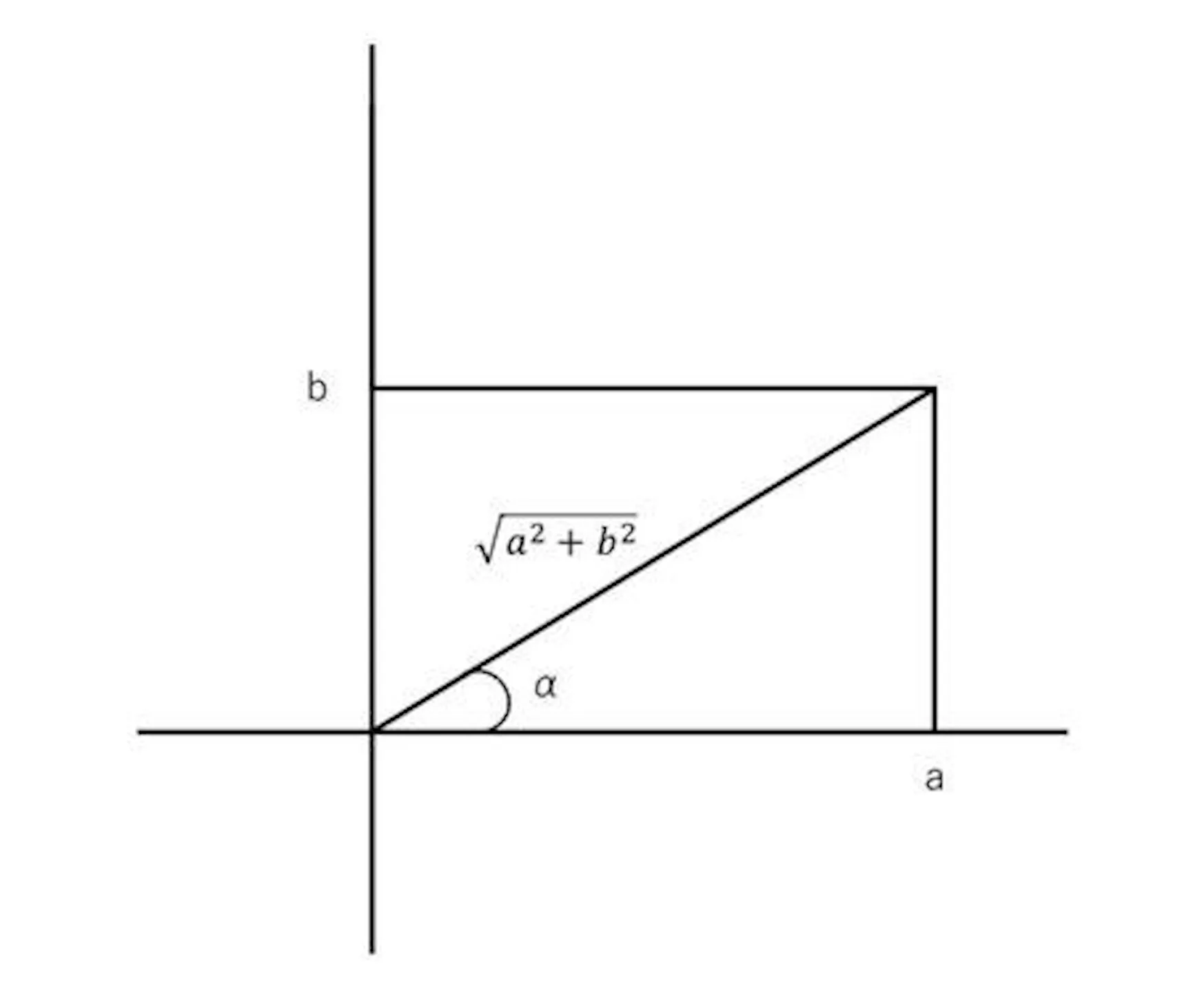
上の図のように原点から$(a,b)$への線分と$(a,b)$から$x$軸への垂線、$x$軸からできる直角三角形について考えてみましょう。

斜辺の長さは$\sqrt{a^2 + b^2}$となるため、$\sin \alpha$と$\cos \alpha$はそれぞれ上の式で表すことができます。ピタゴラスの定理から2乗の和の平方根を取り、それぞれの値を割ることで三角比としていたということです。

練習問題

1.$\sin \theta = \dfrac{3}{5}$のとき$\cos \theta$の値を求めなさい。

1の解答

$\sin^2 \theta + \cos^2 \theta = 1$より
$\cos \theta = \pm \sqrt{1 - \sin^2 \theta} = \pm \sqrt{1 - \left(\dfrac{3}{5}\right)^2} = \pm \sqrt{1 - \dfrac{9}{25}} = \pm \sqrt{\dfrac{16}{25}} = \pm \dfrac{4}{5}$

2.次の式を簡単にせよ。$\sin(-\theta),\cos(-\theta),\tan(-\theta)$

2の解答

$\sin (-\theta) = -\sin \theta$
$\cos(- \theta) = \cos \theta$
$\tan(-\theta) = -\tan \theta$
(三角比の対称性)

3.$\sin(30^\circ + 45^\circ)$の値を、加法定理を使って求めなさい。

3の解答

$\sin (30^\circ + 45^\circ) = \sin30^\circ \cos45^\circ + \cos30^\circ \sin45^\circ$

$ = \dfrac{1}{2} \times \dfrac{\sqrt{2}}{2} + \dfrac{\sqrt{3}}{2} \times \dfrac{\sqrt{2}}{2} = \dfrac{\sqrt{2} + \sqrt{6}}{4}$

4.$\cos75^\circ \cos15^\circ$の値を、積和公式を使って求めなさい。

4の解答

$\cos75^\circ \cos15^\circ = \dfrac{1}{2} \left\{ \cos(75^\circ + 15^\circ) + \cos(75^\circ - 15^\circ) \right\}$

$ = \dfrac{1}{2} \left( \cos90^\circ + \cos60^\circ \right) = \dfrac{1}{2} \left( 0 + \dfrac{1}{2} \right) = \dfrac{1}{4}$

5.$\sin75^\circ + \sin15^\circ$の値を、和積公式を使って求めなさい。

5の解答

$\sin 75^\circ + \sin 15^\circ = 2\sin \dfrac{75^\circ + 15^\circ}{2} \cos \dfrac{75^\circ - 15^\circ}{2} = 2\sin \dfrac{90^\circ}{2}\cos \dfrac{60^\circ}{2} $

$= 2\sin45^\circ \cos30\circ = 2 \times \dfrac{\sqrt{2}}{2} \times \dfrac{\sqrt{3}}{2} = \dfrac{\sqrt{6}}{2}$

6.$\sin \theta = \dfrac{1}{2}$のとき、$\sin 3\theta$の値を求めなさい。

6の解答

3倍角の公式より$\sin3\theta = -4\sin^3 \theta + 3\sin \theta = -4 \times \left( \dfrac{1}{2} \right)^3 + 3 \times \dfrac{1}{2}$

$ = -\dfrac{4}{8} + \dfrac{3}{2} = -\dfrac{1}{2} + \dfrac{3}{2} = 1$

7.$\cos \theta = \dfrac{1}{2}$のとき、$\dfrac{\theta}{2}$の$\sin$の値を求めなさい。

7の解答

半角の公式より$\sin^2 \dfrac{\theta}{2} = \dfrac{1 - \cos \theta}{2} = \dfrac{1}{2}\left( 1 - \dfrac{1}{2} \right) = \dfrac{1}{2} \times \dfrac{1}{2} = \dfrac{1}{4}$

よって$\sin \dfrac{\theta}{2} = \pm \sqrt{\dfrac{1}{4}} = \dfrac{1}{2}$

8.次の式を$R\sin(\theta + \alpha)$の形に変形し、$R$の値と$\alpha$の値を求めなさい。ただし$0 \le \alpha \lt 2\pi$とする
$y = \sqrt{3}\sin \theta + \cos \theta$

8の解答

$y = \sqrt{3}\sin \theta + \cos \theta$

$ = \sqrt{ \left( \sqrt{3} \right)^2 + 1^2} \left( \dfrac{\sqrt{3}}{ \sqrt{ \left( \sqrt{3} \right)^2 + 1^2}} \sin \theta + \dfrac{1}{ \sqrt{ \left( \sqrt{3} \right)^2 + 1^2}} \cos \theta \right)$

$ = \sqrt{3 + 1} \left( \dfrac{\sqrt{3}}{\sqrt{3 + 1}} \sin \theta + \dfrac{1}{ \sqrt{3 + 1}} \cos \theta \right)$ $ = 2 \left( \dfrac{\sqrt{3}}{2} \sin \theta + \dfrac{1}{2} \cos \theta \right)$

ここで$\dfrac{\sqrt{3}}{2} = \cos \alpha,\dfrac{1}{2} = \sin \alpha$とおくと、下の図から$\alpha = \dfrac{\pi}{6}$と分かる.
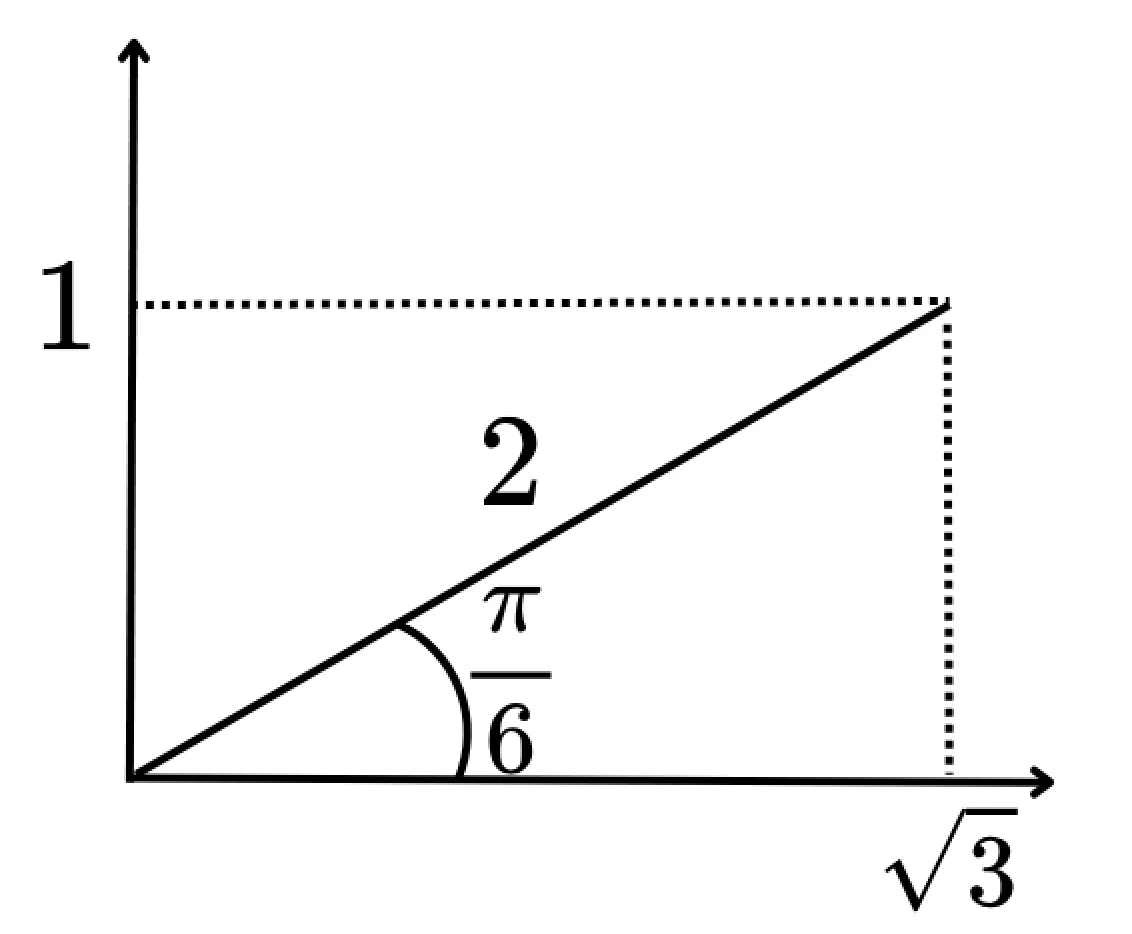練習問題8図よって$y = 2\left( \sin \theta \cos\dfrac{\pi}{6} + \cos \theta \sin\dfrac{\pi}{6} \right) = 2\sin \left( \theta + \dfrac{\pi}{6} \right) $

したがって、$R = 2,\alpha = \dfrac{\pi}{6}$

9.$y = 2\sin \theta - \sqrt{3}\cos \theta$の最大値と最小値を求めなさい。

9の解答

$y = 2\sin \theta - \sqrt{3} \cos \theta$

$ = \sqrt{ 2^2 + \left( -\sqrt{3} \right) ^2} \left( \dfrac{2}{ \sqrt{ 2^2 + \left( -\sqrt{3} \right) ^2}} \sin \theta - \dfrac{\sqrt{3}}{\sqrt{ 2^2 + \left( -\sqrt{3} \right) ^2}} \cos \theta \right)$

$ = \sqrt{4 + 3} \left( \dfrac{2}{\sqrt{4 + 3}} \sin \theta - \dfrac{\sqrt{3}}{ \sqrt{4 + 3}} \cos \theta \right)$ $ = \sqrt{7} \left( \dfrac{2}{\sqrt{7}} \sin \theta - \dfrac{\sqrt{3}}{\sqrt{7}} \cos \theta \right)$

ここで$\dfrac{2}{\sqrt{7}} = \cos \alpha,- \dfrac{\sqrt{3}}{\sqrt{7}} = \sin \alpha$とおくと、

$y = \sqrt{7} \left( \sin \theta \cos\alpha + \cos \theta \sin\alpha \right) = \sqrt{7} \sin (\theta + \alpha) $

$-1 \leqq \sin (\theta + \alpha) \leqq 1$より

$-\sqrt{7} \leqq \sqrt{7} \sin (\theta + \alpha) = y\leqq \sqrt{7}$

したがって$y$の最大値は$\sqrt{7}$、最小値は$-\sqrt{7}$

まとめ

いかがでしたでしょうか。三角関数の公式と導出方法について解説しました。

三角関数はほかの単元だけでなく、ほかの科目でも必要になってくるとても重要な単元です。

三角関数を理解するのはまず三角比をマスターしていないといけないので、三角比の理解が不十分だと思った方は三角関数の基礎である三角比の学習をするようにしましょう。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

明光プラスで読みたい記事のテーマを募集

明光プラスでは読者の方のご期待に沿えるように読みたい記事のテーマを募集しています。ぜひ下のリンクからアンケートにお答えください。

読みたい記事のテーマをリクエストする

あわせて読みたい記事

三角比(sin, cos, tan)とは？覚え方と三角比の表も紹介！

2025.06.20

三角比ではsin(サイン),cos(コサイン),tan(タンジェント)やθ(シータ)といった聞きなれない呪文のような言葉がでてくるうえに、覚えることも多いため苦手意識を持っている方も多いのではないで...
等比数列は簡単！一般項や和の公式を1から解説します

2025.06.06

数Bの数列を学習すると等差数列の次に学ぶのが等比数列です。しかし等比数列に比べて見た目が複雑で規則性も掴みにくいため、苦手意識を持っている人も多いのではないでしょうか。等比数列は漸化式の問題を解くと...
三角形の面積の求め方！学齢に応じた公式の一覧となぜそうなるのかを解説します

2025.06.04

三角形の面積を求める問題は小学生から習いますが、大学入試に至るまでいろいろな求め方を習います。場合によって使い分ける必要がありますが、全てを完全に理解している方は少ないのではないでしょうか。本記事...