2024.07.05

余弦定理についての公式と証明、例題も合わせてやさしく解説します！

余弦定理は数学Ⅰで登場しますが、三角比の理解が浅いまま学習すると、理解があやふやになりがちです。
この記事では、余弦定理の公式やその証明についてわかりやすく解説します。

三角比の理解を深めたい方は、先にこちらの記事をご覧ください。
三角比(sin, cos, tan)入門！表の使い方とわかりやすい公式の覚え方を紹介！

正弦定理についてはこちらからご覧ください。
正弦定理について公式と証明、例題も合わせてやさしく解説します！

余弦定理の公式とは？

余弦定理は、三角形における辺と角度の関係を示す公式です。$cosθ$（余弦）に基づいているため、余弦定理という名前がついています。

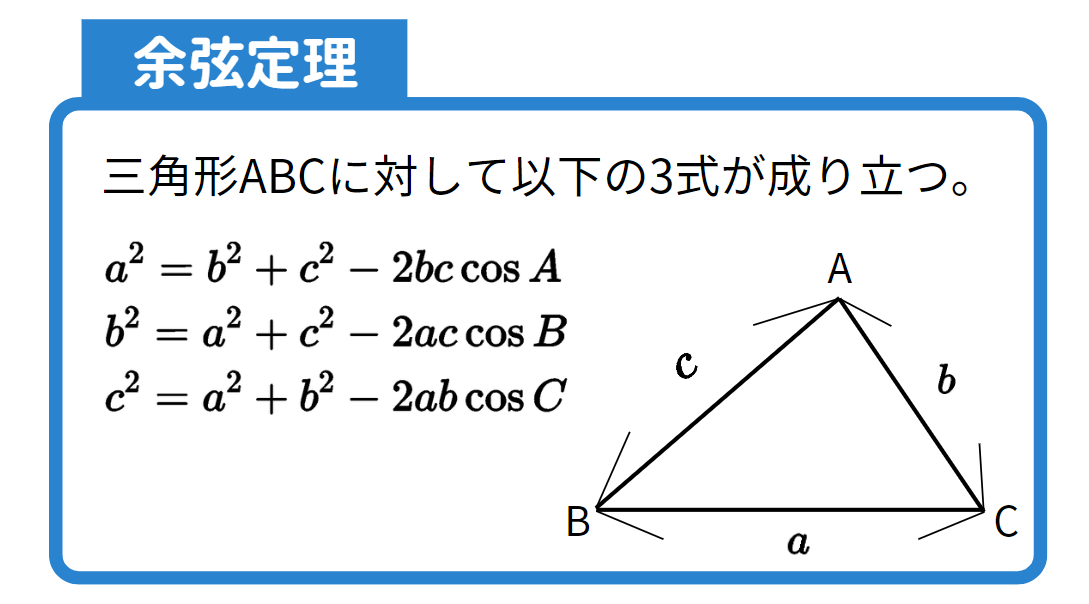
実は、余弦定理と三平方の定理には密接な関係があります。一番下の式で$C$ が$90°$のときを考えると、$cosC=0$ となり、まさに三平方の定理の公式と等しくなることがわかります。
余弦定理は、角度が$0°$から$180°$の間で成り立つ三平方の定理の拡張版と言うことができ、これは直角三角形に限らずどんな三角形にも適応することができます。

三平方の定理の詳細については、以下の記事をご確認ください。
三平方の定理（ピタゴラスの定理）とは？計算の仕方と証明をやさしく解説！

余弦定理は、3辺の長さと1つの角度を変数に持つため、以下の2つのことが言えます。

2辺と1つの角度がわかる場合

2つの辺の長さと1つの角度の$cos$ (余弦)の値がわかれば、残りの辺の長さを求めることができます。

例：辺$a = 1$、辺$b=2$、角$C=60°$のとき、辺$c$の長さは？

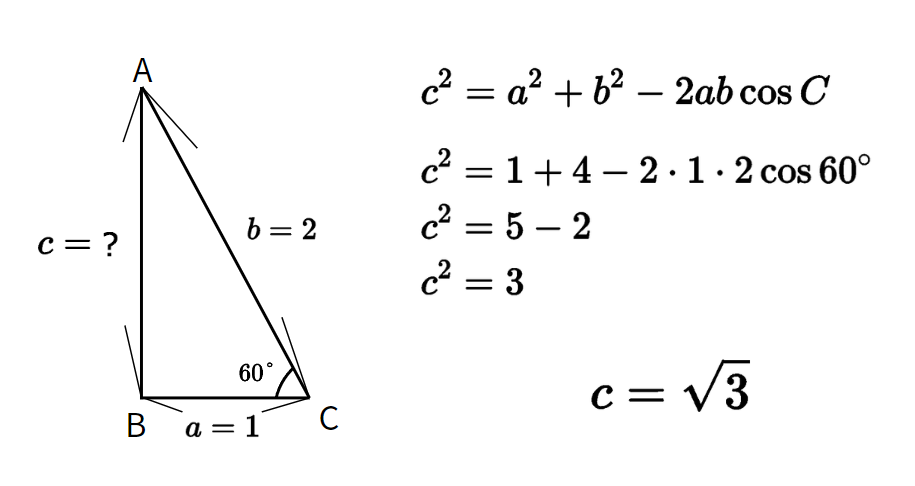
3辺の長さがすべてわかる場合

3辺の長さがわかる場合、どの角度の$cos$ (余弦)でも値を計算することができます。

例：辺$a = 2$、辺$b = 4$、辺$c = 2\sqrt{7}$ のとき、$C$ の角度は？

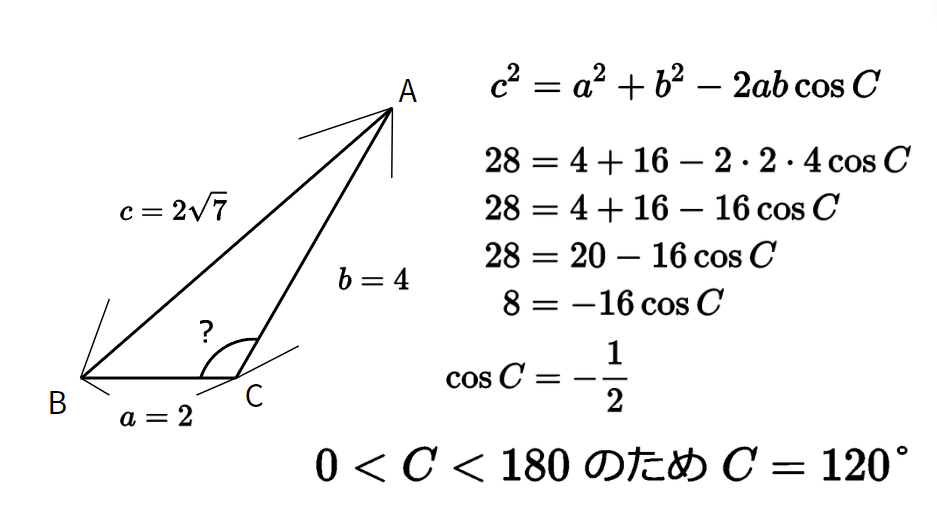
余弦定理はなぜ成り立つのか、証明を簡単に解説

ここからは、余弦定理の証明について簡単に解説していきます。
なお、3つの式は同様に証明できますので、今回は$a^2=b^2+c^2-2 b c \cos A$ の証明について解説します。

鋭角か鈍角かによって証明が変わるため、それぞれのケースについて説明します。
直角の場合はすでに説明した通り、三平方の定理と同じ式になるため、証明は割愛します。

Aが鋭角の場合

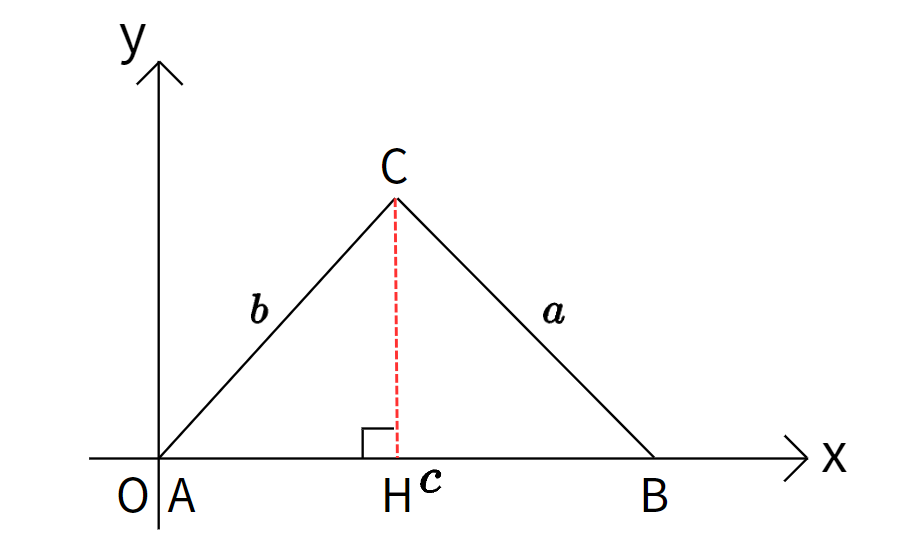
このように三角形を$xy$ 平面に配置し、角$A$ を原点$O$ と合わせ、辺$AB$ を$x$軸と合わせます。
次に、三角比を用いて三角形$CHB$ において三平方の定理を使い、等式を作ることを目指します。

$C$ から$x$軸に垂線を引くと、以下の関係が成り立ちます：
$CH=bsinA$
$AH=bcosA$

また、$BH$ は以下のようになります：
$BH=c-bcosA$

三角形$CHB$ で三平方の定理を使うと、
$a^2 = (c - b \cos A)^2 + (b \sin A)^2$
$\quad=c^2 - 2bc \cos A + (b \cos A)^2 + (b \sin A)^2$
$\quad=c^2 - 2bc \cos A + b^2 (\cos^2 A + \sin^2 A)$

ここで、 $\cos^2 A + \sin^2 A = 1$ を用いると、
$a^2 = c^2 - 2bc \cos A + b^2$

従って、余弦定理の式
$a^2 = b^2 + c^2 - 2bccosA$ が成り立つことがわかります。

Aが鈍角の場合

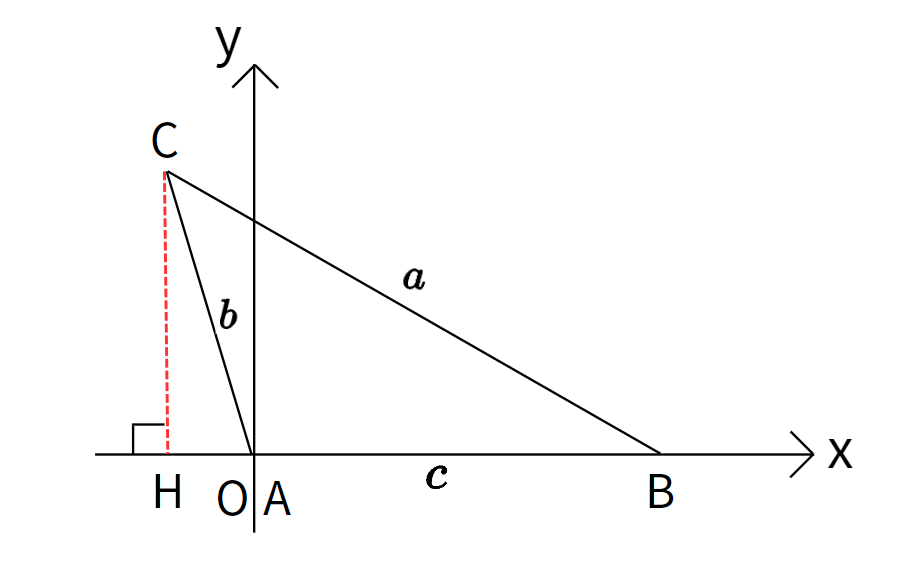
同様に三角形を$xy$ 平面に配置し、角$A$ を原点$O$ と合わせ、辺$AB$ を$x$軸と合わせます。
$AH=-bcosA $ かつ $CH=bsinA$ より、三角形$CHB$ において三平方の定理の式を立てると、次のようになります：
$a^2 = (c - b \cos A)^2 + (b \sin A)^2$

以降はAが鋭角の場合と同様に式変形を行うと、
$a^2 = b^2 + c^2 - 2bc \cos A$ が成り立つことがわかります。

余弦定理の問題を解くコツを例題で解説！

先にも述べましたが、余弦定理は2つのパターンがあります。

①2辺と1つの角度がわかっている場合、残りの辺の長さもわかる（その角度の$cos$の値がわかる場合）
②3辺の長さがすべてわかっている場合、どの角度の$cos$の値もわかる

そのため、問われている値を出すためには、どの値がわかっていて、余弦定理のどちらのパターンが適用できるのかを考える必要があります。以下の例題で確認してみましょう。

パターン①の例題

三角形ABCにおいて、$a=2$、$b=3$、$C=120°$のとき$c$の長さを求めよ。

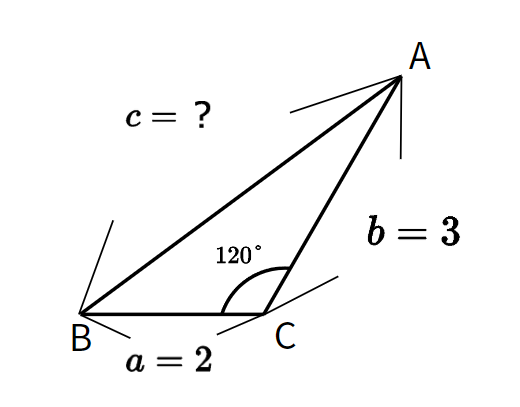
2辺と1つの角度がわかっているため、余弦定理で残りの辺$c$ を導くことができます。

$c^2 = 4 + 9 - 2 \cdot 2 \cdot 3\cdot cos120°$
$c^2 = 13 - 12 \cdot (-\frac{1}{2})$
$c^2 = 19$
$\; c = \sqrt{19}$

パターン②の例題

三角形ABCにおいて、$a=7$、$b=15$、$c=13$ のとき$Ｃ$の角度を求めよ。

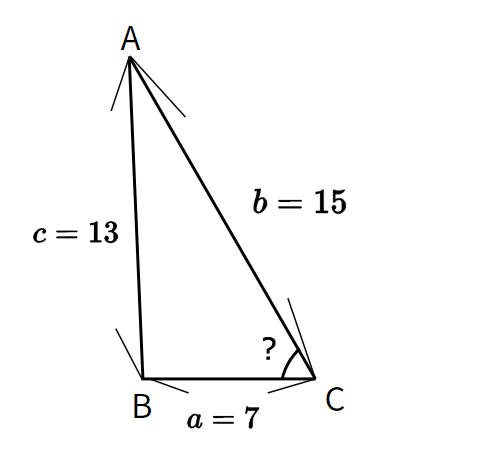
3辺の長さがわかっているため、$cosC$ の値を導くことができます。

$\quad 169 = 49 + 225 - 2 \cdot 7 \cdot 15 \cdot cosC$
$-105 = - 210cosC$
$cosC = \frac{1}{2}$

$0° < C < 180°$のため、$C = 60°$とわかります。

まとめ

いかがでしたでしょうか。
本記事では、余弦定理の公式と証明、問題のパターンについて解説しました。

三角比を理解したうえで学習すると、角度を求めるパターンと、辺の長さを求めるパターンの2つを理解すればよいことがわかります。

公式や、今回紹介したパターンがスラスラ出てくるようになるまで、余弦定理の演習問題を繰り返し解くようにしましょう。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

明光プラスで読みたい記事のテーマを募集

明光プラスでは読者の方のご期待に沿えるように読みたい記事のテーマを募集しています。ぜひ下のリンクからアンケートにお答えください。

読みたい記事のテーマをリクエストする

あわせて読みたい記事

最大公約数とは？最大公約数の簡単な求め方を1から解説！

2025.02.13

最大公約数は小学5年生で最初に学習しますが、高校数学の数学Aでも扱います。一見、単純に見える最大公約数ですが、数学Aの整数問題では素因数分解やユークリッドの互除法といったものを用いて求める必要があ...
ユークリッドの互除法とは？計算の仕方や証明をわかりやすく解説！

2025.02.13

最大公約数を求めるときに使えるユークリッドの互除法ですが、なぜこの方法で最大公約数が求められるのかを理解していない人も多いのではないでしょうか。ユークリッドの互除法がなぜそうなるのかを理解しておく...
ルートや平方根について概念や計算方法を1からやさしく解説！

2025.01.30

中学3年生から出てくるルート(√)や平方根は、幅広く使われるため大学受験でも必須の知識です。しっかりと理解しておきたいところですが、なかなか理解できず計算が難しいと感じる方も多いのではないでしょうか...