2024.10.31

平方完成のやり方を簡単解説！平方完成の意味や使いどころ、練習問題を紹介！

中学生で習う平方完成、苦手に感じていたりつまずいたりしてしまう方も多いのではないでしょうか。この記事では平方完成のやり方や、なぜ平方完成が必要なのか、平方完成をするとどういうメリットがあるのかを練習問題も含めて１からやさしく解説します。

平方完成とは？

平方は平方メートル($ m^2 $)などで使うように2乗という意味があり、平方完成は「2乗の形にしてしまう」という意味で理解するとよいでしょう。

平方完成をすることで、二次式の変数を2乗の形で1つにまとめることができ、扱いやすくなります。具体的にはこのような式変換のことを言います。

$ x^2 + 4x + 1 = (x+2)^2 - 3 $・・・①

右辺を展開してみるとわかりますが、左辺と右辺は等しいです。

平方完成のメリットとは？

二次式を平方完成することで、xの二次の項と一次の項を1つにまとめることができます。1つにまとまると扱いやすくなり、いくつかメリットがあります。

二次式の取りうる値の範囲がわかる

先ほどの式①の右辺の$x+2$をあらたな変数$X$と置くと$X^2-3$となります。$X^2\ge0$なので、式①が取りうる値は$X^2=0$ 、つまり $x=-2$のとき最小の$-3$となるため、以下のように言えます。

$x^2 + 4x + 1 = (x+2)^2 - 3\\ ~~~~~~~~~~~~~~~~~~~~\ge-3$

このように平方完成をすることで元の式が取りうる値の範囲がわかります。二次式で最小値や最大値、取りうる値の範囲を問われるときには平方完成を使うと求めることができます。

グラフが書ける

$f(x) = (x+2)^2-3$としたときにこのグラフは、$y=x^2$というグラフをx方向に-2、y方向に-3ずらしたグラフだとわかります。

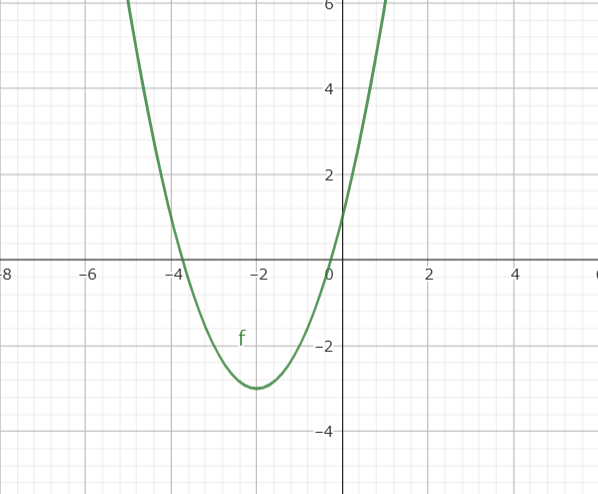
つまり、$y=x^2 + 4x + 1$は下に凸で頂点（-2, -3）を持つ放物線だということがわかります。また、グラフが書けることによりxの定義域が決められているときに、yの値域も求めることができます。

例えば$x \ge0$の場合、この範囲ではxは増加するほどyが増加する形なので、最小値は$x=0$のとき$y=1$で、値域は$y\ge1$となります。

平方完成のやり方を理解する

まず平方完成のやり方をイメージするためにこちらの展開の公式を確認します。

$(x+A)^2 = x^2+2Ax+A^2$・・・②

平方完成は右辺の式を左辺にするイメージで行います。先ほどの式を使って平方完成のステップを確認してみます。
※これから2乗の形で1つにまとめた$(x+A)^2$を平方部分と呼ぶことにします。

$x^2+4x+1$・・・③

②の右辺と③の式の$x$の1次の項の係数を比べてみると、それぞれ2Aと4から、$A=2$で、$x$の係数を2で割ったものだということがわかります。

また、$(x+2)^2$を使うことで$x^2+4x$がひとつにまとめられます。しかしこれを展開すると余計な定数項$A^2=2^2=4$が出てきてしまうため、帳尻を合わせるために-4を加えます。

$x^2+4x=(x+2)^2-4$

つまり③の式は

$x^2+4x+1=(x+2)^2-4+1\\ ~~~~~~~~~~~~~~~~~~~~=(x+2)^2-3$

と平方完成することができます。

ポイント

・ $x$の係数を2で割った値を使って平方部分を作る
・平方部分から出てくる余計な定数項を消すために差し引きする

二次の項に係数がある場合の平方完成

$2x^2+8x-3$のような$x^2$に係数がある式を平方完成する場合について解説します。平方部分は結論から言うとこの形にします。

$2(x+A)^2$

そのためにxを含む項をまず$x^2$の係数でくくります。

$2(x^2+4x)-3$

この括弧の中身を同様に平方完成すると

$2\{(x+2x)^2-4\}-3$

となり、｛｝の中の定数項を外に出して整理するとこのようになります。

$2(x+2)^2-8-3=$$2(x+2)^2-11$

ポイント

・ $x^2$の係数で$x$を含む項をくくる
・くくった部分で平方完成をする
・出てきた余計な定数項を外に出して整理する

平方完成の一般化（公式）

これまで各項の係数が具体的な数字の場合で平方完成を行いましたが、係数が変数のときの平方完成について解説します。文字にすると少し難しい印象になりますが、やることは変わりません。

今までのポイントをおさらいしつつまとめるとこのようになります。

ポイント

・ $x^2$の係数で$x$を含む項をくくる
・くくった部分で平方完成をする
　　・定数項の部分はxの係数を2で割ったもの
　　・余計な定数項を差し引きする
・出てきた余計な定数項を括弧の外に出して整理する

$ax^2+bx+c=a(x^2+\frac{b}{a}x)+c\\ ~~~~~~~~~~~~~~~~~~~~~=a\{(x+\frac{b}{2a})^2-\frac{b^2}{4a^2}\}+c \\ ~~~~~~~~~~~~~~~~~~~~~=a(x+\frac{b}{2a})^2-\frac{b^2}{4a}-c$

このように変数を使った式でも平方完成をすることができ、この概念を使って二次方程式の解の公式を求めることができます。

二次方程式の解の公式は理解しておくと二次方程式の解がいくつあるのかわかったり、公式に当てはめるだけで解が求められるようになるため、理解しておくと便利です。

二次方程式の解の公式についてはこちらの記事で詳しく解説しています。合わせて参考にしてください。
【簡単】二次方程式の解の公式と、判別式についてやさしく解説します！

平方完成の練習問題

平方完成は何度も自分で行うことで慣れてきますので、練習問題を解くことで慣れておきましょう。

xの2次の項に係数がない場合

$x^2+10x+2$を平方完成してください、またこの式が取る最小値はいくつですか。

解答と解説はこちら

分数が出る場合

$3x^2+2x+1$を平方完成してください。

解答と解説はこちら

二次の項の係数が負の場合

$-2x^2-6x+1$を平方完成してください、また$x\gt3$のときのこの式が取る値域を求めてください。

解答と解説はこちら

係数が文字の場合

$2ax^2+3bx+1$を平方完成してください、また$y=2ax^2+3bx+1$としたときのこのグラフの頂点を求めてください。

解答と解説はこちら

まとめ

いかがでしたでしょうか。

平方完成は二次方程式の解の公式のみならず、二次式の取りうる値や、放物線のグラフでもよく使う知識です。ポイントをきちんと押さえれば、どんな場合でも同じように解くことができます。平方完成は何度も問題を解くことで慣れてきます。練習問題をたくさん解いて慣れて内容を理解し、自分のものとしましょう。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

あわせて読みたい記事

三平方の定理（ピタゴラスの定理）とは？計算の仕方と証明をやさしく解説！

2025.07.04

もくじ三平方の定理(ピタゴラスの定理)とは？三平方の定理(ピタゴラスの定理)の応...
連立方程式は簡単！基本問題の解き方から文章題の解き方まで徹底解説します

2025.07.01

連立方程式は中学数学の重要単元で、多くの生徒がつまずいてしまうテーマです。つまずきやすい理由は一元方程式や分数、小数など、これまでに学んだ数学の内容が一挙に出てきて総合力が問われ、また、使う文字や...
因数分解はなぜ必要？因数分解の意味とやり方、公式を1から解説！

2025.06.10

中学3年生や高校の数学で学ぶ「文字と式」の単元で登場する因数分解は、高校数学の基礎となる重要な単元です。さらに、高校入試でも頻出の分野のため、早めに理解しておくことが大切です。共通因数や定数項など...