2024.08.05

素因数分解とは？やり方を問題を交えてわかりやすく解説します！

素因数分解は中学1年生で習う単元ですが、苦手な人も多いのではないでしょうか。素因数分解の考え方やその応用は高校入試でも使いますし、大学入試でも必要です。さまざまなところで使うのでぜひとも理解をしておきたいところです。
最初はやり方がわからないことで難しく感じるかもしれませんが、やり方を身につけて理解をすれば難しい単元ではありません。
この記事では素因数分解とそのやり方を、実際の問題を交えて1からわかりやすく解説します。

素因数分解とは？

素因数分解とはその字の通り、ある自然数を「素数の因数に分解すること」です。素数や因数分解という言葉が理解できている人はこれで理解できるかもしれませんが、もう少しかみ砕いて説明すると、

「ある自然数を素数のみの掛け算の形で表すこと」を素因数分解と言います。

素数についてはこちらの記事で詳しく解説しています。
素数を知らない・理解が浅い場合は先にこちらの記事を先に読むことをおすすめします。

素数とは○○です！覚えておくべき素数一覧や素数の判定法を紹介！

1とその数自身でしか割れない数を素数と言いました。反対に、素数以外は1とその数以外で割れるということになります。その割り算をしてすべて素数の掛け算で表すことを素因数分解と言います。
具体的な例で確認してみましょう。

素因数分解のやり方を紹介

これから素因数分解のやり方を具体的な例で紹介していきます。
420を素因数分解してみましょう。

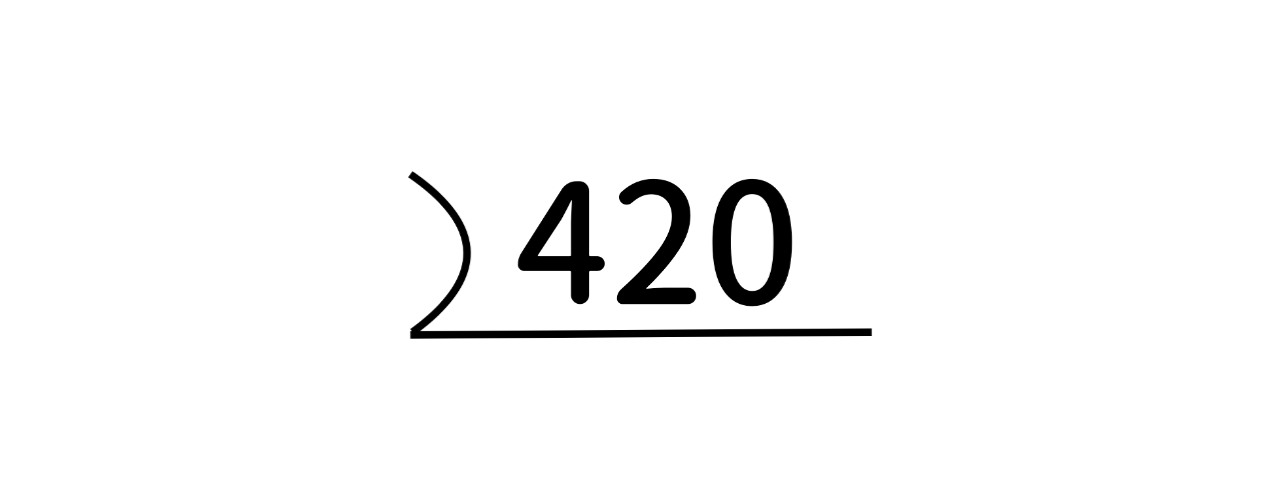
420単体.png

よくやる方法としてまず数字とこのような割り算のひっ算を上下反転したような線を書きます。
素数の判定方法で紹介した方法を用いて、素数の小さい順で割り算をしていきます。

420の場合、2が一番小さい素数の約数となります。
そのため、このように左に2と書き、下に割り算の結果を書きます。

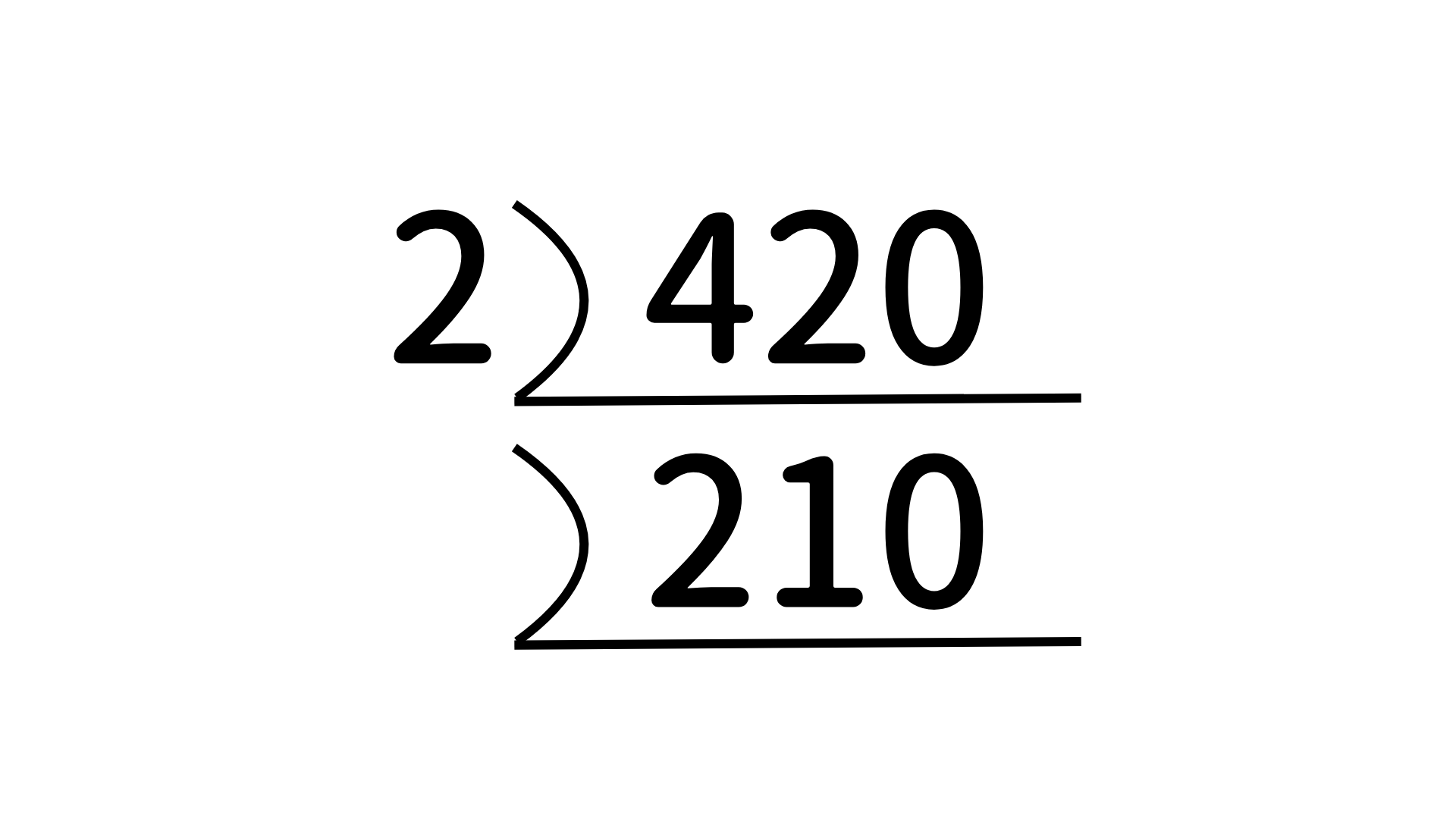
%E7%B4%A0%E5%9B%A0%E6%95%B0%E5%88%86%E8%A7%A3-3.png

210も2で割れるため同じように結果を書きます。

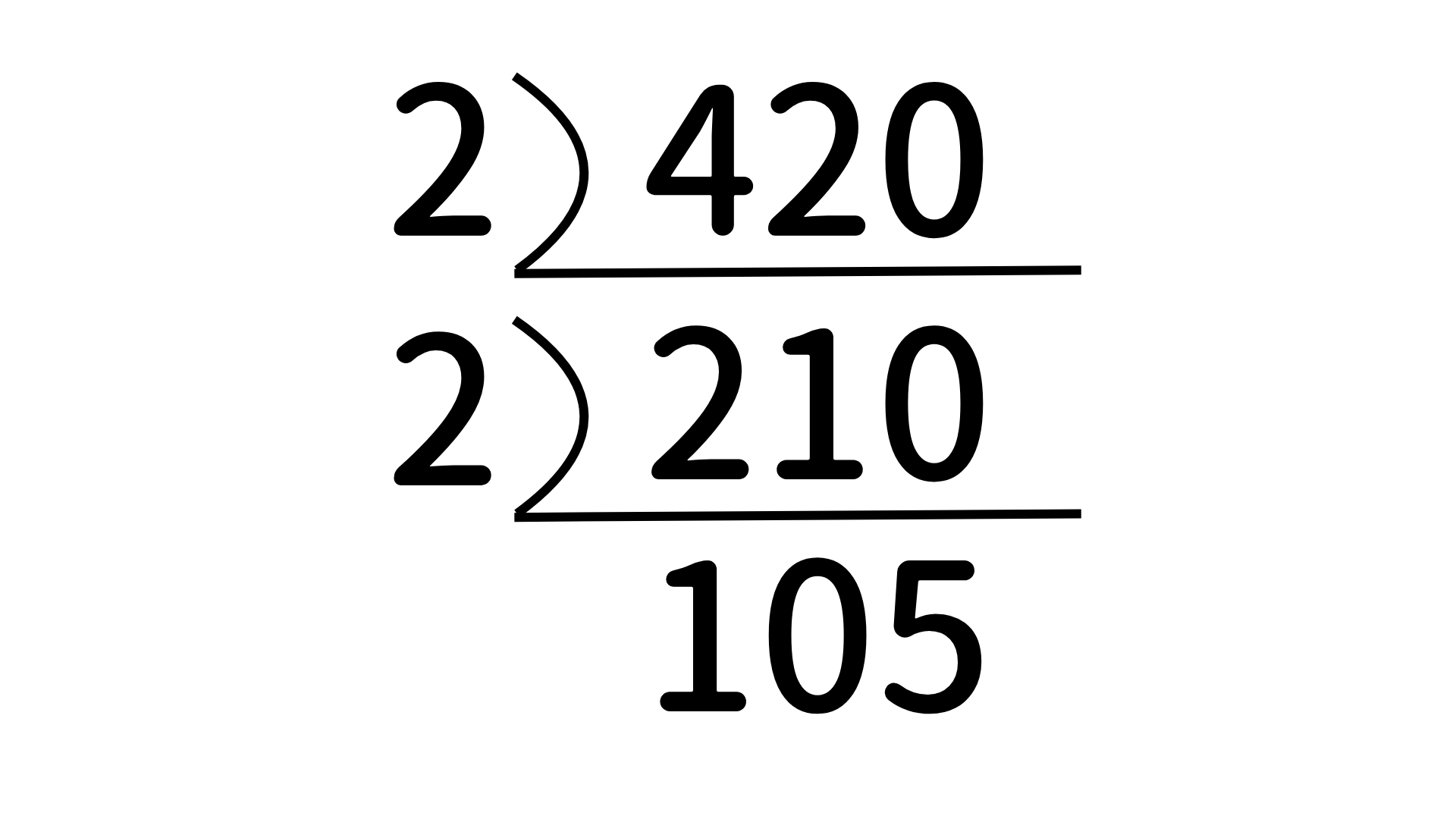
%E7%B4%A0%E5%9B%A0%E6%95%B0%E5%88%86%E8%A7%A3-4.png

105となりました。奇数なので2で割れなくなりましたね。2の次に小さい素数である3で割れるかを確認すると1+0+5は6となり3で割れるため、105は3で割れます。左に3と書くと、

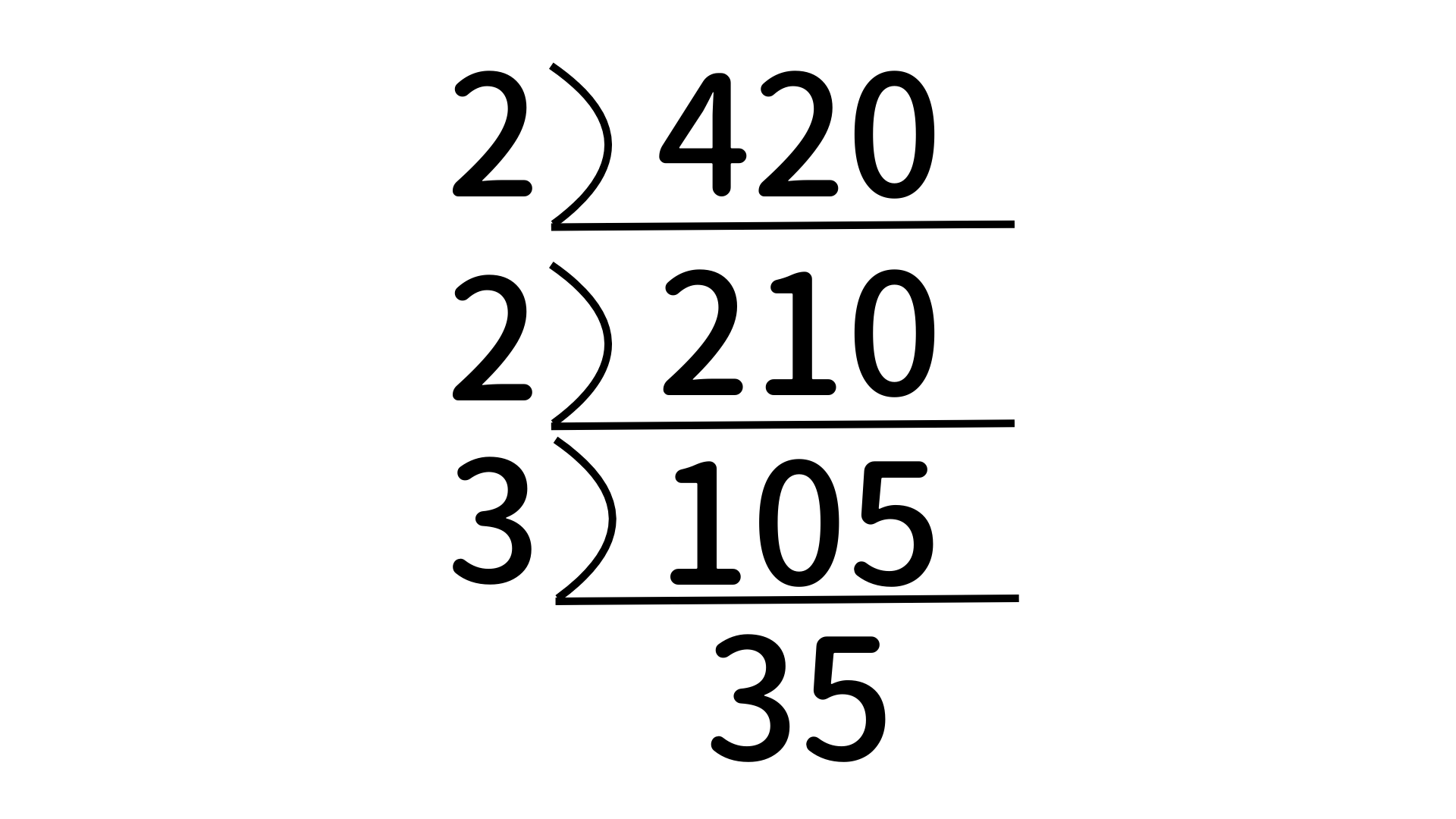
%E7%B4%A0%E5%9B%A0%E6%95%B0%E5%88%86%E8%A7%A3-5.png

割り算の結果は35となります。35は3+5が8のため3で割れません。末尾が5なので、3の次に小さい素数である5で割れることがわかります。

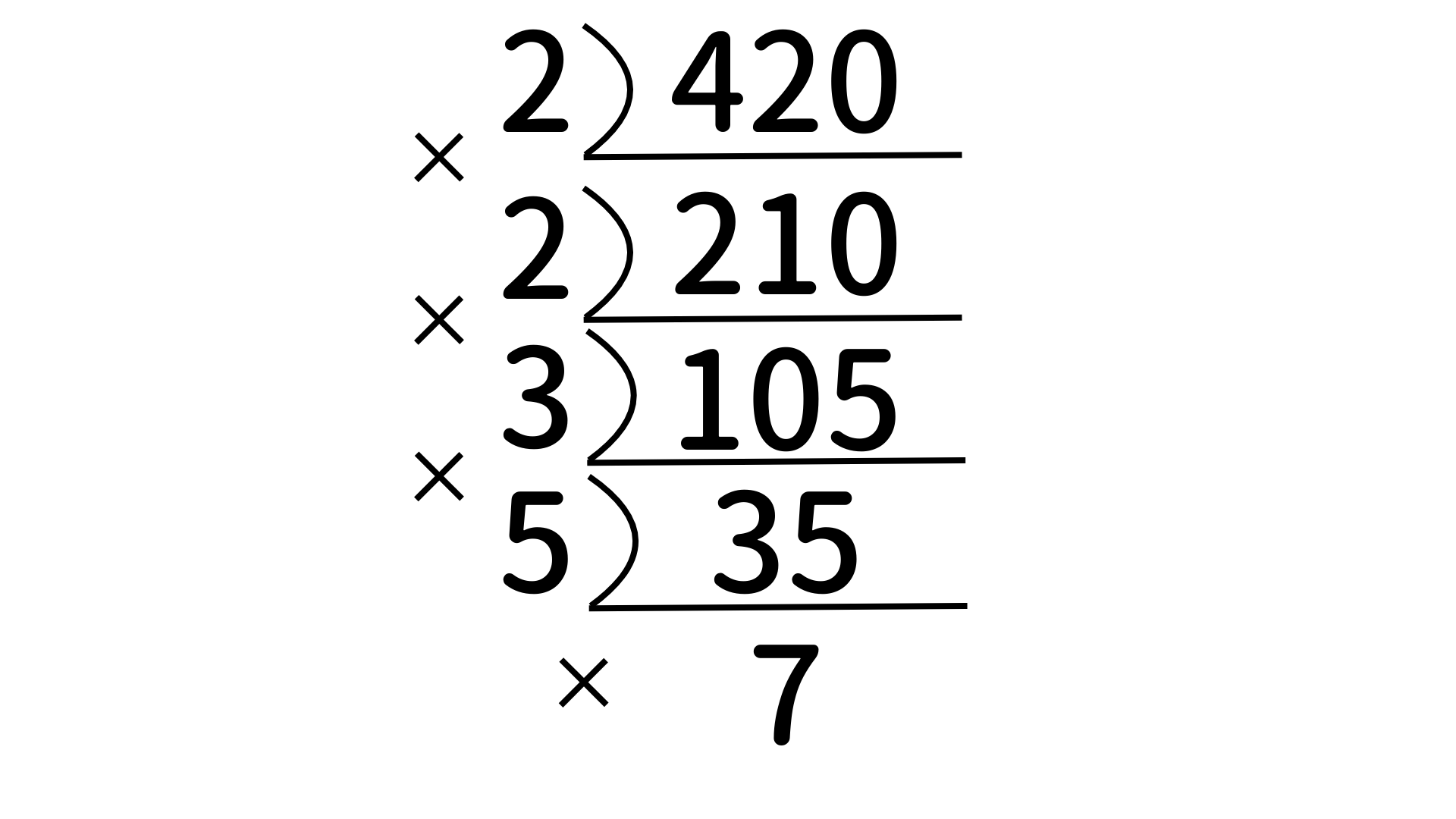
%E7%B4%A0%E5%9B%A0%E6%95%B0%E5%88%86%E8%A7%A3-7.png

7は素数ですね。これで420は$2 \times 2 \times 3 \times 5 \times 7$と表せることがわかりました。
2が2つあるため指数を使ってまとめます。

$420=2^2×3×5×7$

素因数分解のやり方をまとめるとこのようになります。

%E3%81%AE%E3%81%A8%E3%81%8D.png

素因数分解の応用問題を紹介

素因数分解を応用すると一見難しい問題も簡単に解くことができます。
素因数分解すると何がうれしいか、いくつかの応用問題を通して紹介していきます。

自然数の2乗かどうかを判断できる

420はある自然数の2乗かどうかを確認しましょう。
先ほどの通り420は$420=2^2×3×5×7$と表せます。しかし、3,5,7の指数が奇数のため自然数の2乗では表すことができません。
例えば$420×3×5×7$とすると$420×3×5×7=2^2×3^2×5^2×7^2$となり、$(2×3×5×7)^2$と表すことができるため、$420×3×5×7$は自然数の2乗と言えます。

これに関連してよく出る問題としてはこのような問題です。

420にできるだけ小さい自然数nをかけその積がとある自然数の2乗になるようにするとき、nの値を求めなさい。

その答えは$3×5×7$、つまり105となります。素因数分解した形に奇数の指数が無ければ、その自然数は自然数の2乗で表すことができると理解しておきましょう。

約数の個数を求められる

12の約数の個数を答えなさいというような問題であれば、1,2,3,4,6,12と数え上げて6個と答えることができますが、420の約数をすべて答えるとなると少し大変です。
その場合は素因数分解と組み合わせを使って求める方法があります。

$420=2^2×3×5×7$

それぞれの素因数をどれだけ使うかという考え方で約数のパターンが何通りあるかを考えていきます。
例えば6という約数2×3で2と3を1つずつ、5と7は使っていない（0個使っている）と考えられます。
$6 = 2^1×3^1×5^0×7^0$
このように素因数(素数の因数)の指数のパターンを計算するという考え方です。

2	$2^0$か$2^1$か$2^2$の3通り
3	$3^0$か$3^1$の2通り
5	$5^0$か$5^1$の2通り
7	$7^0$か$7^1$の2通り

よって組み合わせの数は
3(2の指数のパターン)×2(3の指数のパターン)×2(5の指数のパターン)×2(7の指数のパターン)
=24通りとなり、420の約数の数は24個となります。

公式としてはこのように表されます。
素因数分解-9.png このように約数の個数を数えるのが大変な場合は素因数分解を応用すると覚えておきましょう。

まとめ

いかがでしたでしょうか。
本記事では、素因数分解について解説しました。

素因数分解はやり方さえ覚えてしまえば簡単です。先ほど紹介した約数の個数を求める問題などある程度パターン化された問題もあるため、やり方を覚えて練習すればスムーズに問題を解くことができるようになります。

素因数分解は高校入試のみならず、大学入試でも使う重要な単元です。確実に内容を理解し、自分のものにしましょう。

教室数・生徒数No.1の個別指導塾！

明光義塾では、勉強の進め方や、勉強計画の立て方など、学習の質を高めるための豊富なノウハウを持っています。お子さまの抱える課題に向き合いながら、目標に向かって効率的な勉強を行えるようサポートできます。

お子さまの現状の課題を知りたい方、お子さまの更なる成長をお考えの方は、ぜひ一度お近くの明光義塾までお気軽にご相談ください。

近くの教室を探す

あわせて読みたい記事

三平方の定理（ピタゴラスの定理）とは？計算の仕方と証明をやさしく解説！

2025.07.04

もくじ三平方の定理(ピタゴラスの定理)とは？三平方の定理(ピタゴラスの定理)の応...
連立方程式は簡単！基本問題の解き方から文章題の解き方まで徹底解説します

2025.07.01

連立方程式は中学数学の重要単元で、多くの生徒がつまずいてしまうテーマです。つまずきやすい理由は一元方程式や分数、小数など、これまでに学んだ数学の内容が一挙に出てきて総合力が問われ、また、使う文字や...
因数分解はなぜ必要？因数分解の意味とやり方、公式を1から解説！

2025.06.10

中学3年生や高校の数学で学ぶ「文字と式」の単元で登場する因数分解は、高校数学の基礎となる重要な単元です。さらに、高校入試でも頻出の分野のため、早めに理解しておくことが大切です。共通因数や定数項など...